| Issue |
JNWPU
Volume 42, Number 5, October 2024
|
|
|---|---|---|
| Page(s) | 882 - 890 | |
| DOI | https://doi.org/10.1051/jnwpu/20244250882 | |
| Published online | 06 December 2024 | |
IDE-SVM algorithm and it's usage in physical layer security method for IoT
IDE-SVM算法及其在物联网物理层安全中的应用
1
China Information Consulting and Designing Institute Co., Ltd., Nanjing 210019, China
2
Nanjing University of Posts and Telecommunications, Nanjing 210003, China
Received:
22
September
2023
To address the problem that there is no standard for the parameter selection of support vector machine (SVM) algorithm, a parameter optimization selection method based on the integrated improved differential evolution (IDE) algorithm is proposed, which uses the minimization of the classification error rate as the optimization criterion and the improved differential evolution algorithm to optimize the combination of SVM parameters to obtain an SVM algorithm with higher classification accuracy. At the same time, to avoid the basic DE algorithm from falling into local optimum when solving the SVM parameter selection problem and to improve the search efficiency of the DE algorithm. In this paper, an improved differential evolutionary algorithm is proposed to obtain a DE algorithm with faster convergence and higher accuracy by using the circular arc function for adaptive control of the variance scaling factor F and the crossover probability factor R, combining with the random newborn individual replacement operation. Based on this, an IDE-SVM IoT physical layer security method based on IDE-SVM is proposed. The experimental results show that the authentication accuracy of the physical layer security method based on the improved SVM algorithm is higher than others.
摘要
针对支持向量机(support vector machine, SVM)算法参数选择没有标准的问题, 提出了一种基于综合改进差分进化算法(improve differential evolution, IDE)的参数优化选择方法, 以分类错误率最小为优化准则, 利用改进的差分进化算法实现SVM参数的组合优化, 获得了一种更高分类精度的SVM算法。为了避免基本DE算法在求解SVM参数选择问题时陷入局部最优, 提高DE算法的搜索效率, 提出了一种改进差分进化算法, 通过使用圆弧函数对变异缩放比例因子F以及交叉概率因子R进行自适应控制, 同时结合随机新生个体替换操作, 得到一种收敛速度更快、精度更高的DE算法。在此基础上, 提出了一种基于IDE-SVM物联网物理层安全方法。实验结果表明基于改进后SVM算法的物理层安全方法认证准确率更高。
Key words: physical layer security / support vector machine / differential evolution / parameter optimization
关键字 : 物理层安全 / 支持向量机 / 差分进化 / 参数优化
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
在无线终端到无线基站的安全接入问题上, 传统方法采用上层协议对其进行加解密。然而, 这种方法会消耗大量系统资源, 增加通信时延, 也容易被计算能力更强的恶意攻击者破解。同时, 这种方法默认物理层本身安全的条件有待论证, 用于传输密钥的信道安全难以保障[1]。
事实上, 由于衰落信道的时变性、唯一性、信道互易性、位置互异性等特性, 每个用户的物理层信息就类似用户的“指纹”, 是独一无二的, 因此可以利用物理层信息(包括大尺度衰落因子、信号到达时间等)对用户进行接入鉴权。这种方案直接利用了通信过程中的信道估计信息, 不需要额外传输信息, 其安全性不依赖算法的复杂度, 因此消耗算力较低, 理论上在一定通信的信息量下不可被破解[2]。
目前的物理层认证方法大多基于信道信息的先验知识[3]。随着5G应用的普及, 物联网接入设备爆发式增长, 物理层信息量激增。利用机器学习算法可以高效地对物联网终端物理层的海量数据进行规律分析和特征提取, 建立基于机器学习算法模型的物理层安全接入认证方式。无需事先知道关于信道的先验知识, 模型以信道观测数据为基础, 通过“自适应”的认证方式安全接入网络[4]。
尽管机器学习中有很多复杂的算法, 但物联网节点的算力有限, 无法使用复杂的算法[5]。SVM算法简单高效、泛化能力强, 对数据规模和数据分布的要求低, 在小样本训练集上比其他算法性能更好。采用SVM算法在基站中建立物理层安全接入认证模型, 直接通过信号与信道包含的信息在物理层进行安全接入鉴权。
在二分类问题中，SVM目标是在特征空间内寻找1个超平面，该超平面能够最大化地分隔开2个不同的类别[6]。然而数据中往往存在不能满足理想线性分隔约束条件的异点, 为了调整分类超平面对于分类误差的关注程度, 引入错误惩罚参数C。C取值大时对损失函数对误分类的样本惩罚增大, 少数样本对决策面的影响增加, 因此可能造成过拟合现象, C取值小时损失函数对误分类的样本惩罚减小, 则可能造成相反的“欠学习”现象[7]。另一个问题是: 利用信道特征分类这一问题是非线性的, 因而需要通过核函数ϕ对特征进行非线性变换, 将特征映射到一个新高维特征空间中去, 从而将非线性问题变换为线性问题, 最后用线性分类的方法在新空间中寻找一个超平面对特征进行分类。核函数的映射能力受到核函数参数g的影响。目前来看, 优化支持向量机(support vector machine, SVM)算法的参数优化所面临的主要问题是对于核函数参数g和错误惩罚参数C的调优, 这2个参数直接影响算法学习能力、分类精度和泛化能力[8]。
现有该参数选择问题的研究弊端很明显, 比如文献[9]提出了一种基于禁忌列表遗传算法的SVM改进方法, 但该方法需求算例多, 耗时长且需要一直更新禁忌表; 文献[10]提出了使用粒子群优化和遗传算法的SVM参数选择方案, 但是, 方案都存在干扰操作实时性不高的问题; 文献[11]提出了利用网格搜索算法进行参数组合寻优, 但网格搜索步长对准确率和速度的影响很大, 步长难以控制, 制约算法运算速度和准确性。
文献[12]提出了基于差分进化算法的参数组合寻优方案, 避免了上述方法的一些问题, 但差分进化算法有自身的性能缺陷, 会造成最终找不到最优参数组合。文献[13]基于此也对差分进化算法做出了相关改进, 但算法改进方向过于单一化, 导致收敛慢, 性能提升较小, 不能最大地避免陷入局部最优解, 在SVM参数寻优的应用中并不理想。因此, 本文在差分进化算法的基础上, 又提出了一种新的基于改进差分进化算法(improved differential evolution, IDE)的SVM参数智能化选取方法(IDE-SVM)。
1 基于IDE-SVM算法的物理层信息的安全接入方法
1.1 SVM算法及其参数组合优化
1.1.1 基于DE算法的SVM参数优化方法
1) DE算法的基本原理
DE是基于群体智能理论, 通过群体内个体间的相互合作、竞争进而产生的智能优化搜索算法, 是一种随机启发式搜索算法。变异、交叉和选择是DE算法的3个核心操作, 其关键思想在于对当前种群中的每一个向量, 都要通过种群中另外2个随机选择的不同向量来进行干扰。
使用DE算法处理函数的优化问题, 对于最小化函数问题minf(x), 假设有x=[x1, x2, …, xd], 其中d是该函数优化问题的维数, 对于向量x, 其第k维参数变量具有上下界限: lk≤xk≤uk(k=1, 2, 3, …, d), 差分进化算法所生成的种群中每一个个体都是该函数优化问题的一个解xi=[xi1, xi2, …, xid], xi表示算法种群中的第i个个体, 从给定的约束范围内中, 随机选择初始化种群个体, 建立优化搜索的初始选择点。假定所有初始化种群都是符合均匀概率分布的, 那么初始化种群操作则如(1)式所示。
式中：rand[0, 1]表示0~1之间的随机数; N表示种群规模, 即随机产生了N个个体组成了初始种群。
标准差分进化算法的变异成分是父代的差分矢量, 当下种群中的每个个体xi(g)都会经过变异产生新的个体vi(g), 其中g表示该种群进化到的代数。不同的DE算法方案会有不一样的变异个体的生成方法, 标准差分进化算法变异操作如(2)式所示。
式中, 序号i, r1, r2, r3都不相同, F为变异算子, 是一个取值范围为[1, 2]的实常数, 用以控制偏差变量的放大作用。由(2)式可知, F越大, 基向量xr1(g)变异越多, 种群多样性越丰富。
变异操作结束后将开始交叉操作, 交叉的目的是增加干扰参数向量的多样性, 避免早熟。每一个变量都需要生成一个位于0~1之间均匀分布的随机数。根据判定条件, 交叉操作选择接受目标个体的对应分量还是保留当前个体的对应分量。交叉操作如(3)~(4)式所示。
式中：rand b(j)表示生成[0, 1]之间第j个随机数; rnbr(i)∈(1, 2, 3, …, d)表示一个随机选择序列, 保证uij(g)从vij(g)处获得至少一个参数。交叉算子R∈[0, 1], 分析交叉操作公式可知: R取值影响着种群的多样性和收敛速度, R越大, rand b(j)≤R的概率越大, uij(g)中参数由vij(g)提供的就越多, 有利于局部搜索和加速收敛速率。R越小则相反, 会增加种群多样性, 有利于全局搜索。
选择操作相对简单, 决定uij(g)能否替代xij(g)成为下一代种群个体, 假设uij(g)的适应度函数值为p, xij(g)的适应度函数值为q, 适应度函数值越大越好。DE算法依照贪婪准则, 将uij(g)的适应度函数值与xij(g)的适应度函数值相比较, 优胜者则成为下一代种群个体。如(5)式所示
通过贪婪准则, 在这种选择机制下, 能够保证第g+1代种群都比第g代相对应的个体好或者一样, 如此逐步搜索找到最优解。
2) IDE算法的原理与优势
参数自适应改进: DE算法随着迭代次数的增加, 种群多样性下降, 有早熟收敛的缺陷。根据上述分析可知, DE算法参数的设置对搜索性能有一定影响。DE算法中的参数有: N, F以及R。N的选取直接影响算法的搜索结果, N值越大, 全局搜索的最优解越好, 但种群规模增加会导致算法消耗更多的系统资源, 降低搜索效率。F和R参数的调节对算法搜索效率的影响较小。
然而, DE算法针对F与R, 都是依据经验设定一个常量, 对于实际中不同的优化问题, 使用常量显然不能使算法的精度达到最佳。根据算法原理分析, 不难发现要使算法性能增强, 避免早熟, 参数F需要在算法搜索早期具有较大值, 通过增加个体间差异来降低算法陷入局部最优的概率; 而在搜索后期, F要取较小值, 使算法向最优解方向搜索, 加快收敛。参数R则相反, 在前期要保持较小值, 后期保持较大值。这样在前期加强全局搜索, 定位出全局最优解的搜索区间, 减少不必要的计算, 到后期加快向最优解聚焦。因此, 本文提出了一种针对DE算法控制参数的自适应改进方案, 在F与R各自的取值范围内, 利用圆弧函数, 将2个参数的取值与当前迭代次数联系起来, 具体改进方法如(6)式所示
式中：g为当前迭代次数；G为设定的终止迭代次数，F∈[0, 2], R∈[0, 1]。
变异操作改进: 将DE算法常用变异机制相结合, 使变异机制在搜索前期更侧重于随机个体xr1(g), 保持种群多样性, 而在搜索后期侧重当前最优个体xbest(g), 加快算法收敛，如(7)式所示。
式中：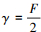
, xr1(g)为当前种群随机个体; xbest(g)为当前种群最优个体; best, r1, r2, r3, r4, r5互不相同。
选择操作改进: 为了确保进化向正确的方向进行, DE算法选择操作依照贪婪准则, 将生成的uij(g)的适应度函数值与xij(g)的适应度函数值一一对应比较, 这样可以保证下一代种群比上一代优秀, 即当ui1(g)的适应度函数值优于xi1时, xi1(g)被淘汰, 但是如果xi1(g)的适应度函数值是剩余所有个体中最好的或是较优的, 那么当出现这种2个优秀个体相比较情况时, 必然会损失一个临时较优解, 不利于搜索向较优方向进行, 也降低了算法搜索效率。因此, 本文提出一种新的选择方案, 即优秀个体保留, 低劣个体去除的方法。将ui(g)与xi(g)的所有个体合并起来, 共2N个, 按照适应度函数值排序, 将排序后的前10%优秀个体保留下来, 末10%的较差个体全部去除, 在剩余80%的个体中先按照标准选择机制一一对应比较选择, 使N保持不变。若存在多余个体, 则按适应度函数值排序末位淘汰, 最终组成新一代种群。该方法不仅能够保存优秀个体, 避免退化现象的发生, 还能剔除最差个体加快差分进化速度。
随机新生个体替换操作: DE算法之所以会陷入局部最优, 其本质是随着迭代次数的增加, 种群个体间的差异性逐渐缩小, 出现了聚焦现象。在此引入种群个体适应度函数值方差的概念, 假设种群个体数为N, 第i个个体的适应度函数值为fi(g), 当前种群的平均适应度函数值为faverage(g), 那么定义该方差为δ2, 如(8)式所示
适应度方差δ2是用来描述当前种群的聚集状态, δ2越大说明种群个体间差异性越大, δ2越小则说明种群聚焦程度严重, 若δ2=0, 那么此时算法就很可能陷入了局部最优。为了使算法能够跳出局部最优解, 继续进行有效搜索, 为方差设定一个阈值τ, 假设设定的终止迭代次数为L次, δ2≤τ的次数记为c, 每有一次δ2≤τ, c=c+1;每有一次δ2>τ, c=0。在迭代到⌊L/2」次之前, 若连续M次迭代都有δ2≤τ, 即c=M, 就判定算法陷入局部最优, 则随机生成k个新个体, 替换当前种群中第1~k个个体。其中⌊x」为向下取整, τ∈[0, 1], M∈[5, 10], k≤⌊N/10」。
1.1.2 基于改进差分进化算法的SVM参数组合优化
1) 参数选择对SVM性能影响分析
非线性SVM算法的性能优劣很大程度上取决于惩罚参数C和核函数参数g的取值。核函数的参数直接影响样本数据在高维特征空间中分布情况。特征子空间的维数越高, 得到的最优分类超平面就会越复杂。因此, 只有通过使用合适的核参数才能得到合适的特征子空间, 从而使SVM分类器具有高效精确的分类能力。因此, 核函数参数g及错误惩罚参数C的好坏对SVM性能有巨大影响。
2) IDE-SVM算法
采用高斯核函数, 定义误判率为种群个体适应度函数, 误判率最小为优化目标, 如(9)式所示
式中：B1, B2分别为2类样本的总数; A1, A2分别为2类样本的误判数目; a为缩放因子, 用来调节适应度函数值变化的明显程度。IDE-SVM算法具体步骤如下:
第1步 初始化种群, 对参数(L, N, F, R, τ, M, k)进行设置, 设置C和g的取值范围, 并依据取值范围随机生成N组(C, g), 作为初始种群xi(g)。
第2步 以第一步中获得的(C, g)作为SVM算法的参数, 对样本数据进行训练和检验, 并得到样本的分类结果, 依据(9)式计算适应度函数值。
第3步 依据(7)式开始变异操作, 生成临时解vi(g)。
第4步 依据(4)式, 进行交叉操作, 生成新解ui(g)。
第5步 依据(9)式计算新解ui(g)种群的个体适应度函数值, 并将其与当前种群xi(g)合并排序, 按照改进的选择操作进行选择, 生成临时下一代种群ti(g+1)。
第6步 依据(8)式计算种群ti(g+1)的个体适应度方差δ2, 对当前迭代次数和方差进行判定, 决定是否进行随机新生个体替换操作, 设替换操作后的种群为si(g+1)。若不需替换, 则xi(g+1)=ti(g+1), 否则xi(g+1)=si(g+1)。
第7步 如果达到了终止条件, 输出SVM最优参数组合(C, g), 否则转至第2步。
1.2 问题场景模型
考虑一个基站、一个合法的物联网无线终端及一个非法终端。令τA为合法终端的信道特征向量
式中, 下标N代表每帧信号均匀采样的样本个数。合法无线终端正在向基站发送信息, 此时非法信号尝试接入, 基站需要从接收到的信号中找出合法信号。假设需检测信号的信道特征向量为
式中：下标f表示需要鉴别发送者的身份；m表示需要检测帧的编号。
研究中有如下假设: ①非法信号源与合法无线终端相距一个波长以外, 此时非法终端与合法终端信道不同。对于5G通信系统, 波长为厘米级或者毫米级, 所以非法信号源必然处于距与合法无线终端一个波长以外的距离。②无线终端的信道是慢衰落的。这个假设在终端设备不是高速移动的情况下是成立的。
根据上述假设, 终端安全接入认证问题可以用假设检验问题表示。在无线基站侧建立已检测的合法无线终端的信道特征作为先验信息, 对连续的信道特征进行相似性检测, 判断其是否来自于合法无线终端。首先需要进行假设检验的就是首个信道特征信号帧的特征参量τf(1), 即
同时, 利用接收到的信道特征参量对SVM进行训练, 并对随后接收到的信道向量进行检验。因此, 基于信道的认证问题可以表示为: 利用合法终端已判决的信道向量τA(i-1), 判断下一个连续的信道向量τA(i)是否来自于合法终端[14]。
1.3 物理层特征提取
在5G大规模天线通信系统中, 使用多天线列阵, 使得不同信号到达接收端的时间、大尺度衰落因子和到达接收天线的到达角也不同, 因此这3个物理层参数适合用于信号安全接入认证。
信号到达时间t: 信号从发送端到接收端所经历的时间, 为了设置门限值更容易, 对t做如下变换
信号的大尺度衰落因子: 假定符号φ(τ)表示信道τ的大尺度衰落因子。同样对φ(τ)做如下变换
信号到达角和信号到达高度角: 假设第m个用户第i个到达角为θm, i, 导向矩阵记为Rm, 采用矩阵的二范数来反映其特征
同样做如下变换
这样, 第i帧的特征向量就可表示为
如此, 比较2个信道向量的相似性就通过xi来完成。
1.4 安全接入方法流程
图 1为物理层安全接入方法流程图。
具体步骤如下:
1) 提取信号的特征值(x1, x2, …, xn), 同时与信号明确合法与否的标签yk构成特征向量{xi|xi∈R2, yi∈{-1, 1}}, 并将其视作训练样本集合。
2) 在离线训练阶段, 用上述样本集合作为模型输入来求解二次规划方程并寻找最优超平面。
3) 在测试阶段, 提取接信号的物理层特征并组成特征向量, 使用训练过的SVM对信号来源是否合法做出判定。
4) 再学习阶段, 将已分类的合法和非法无线终端的特征向量加入原先样本集再次训练SVM, 这样做是为了适应用户信道的缓慢变化。
 |
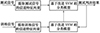图1 无线终端安全接入方法流程图 |
2 实验分析
2.1 IDE算法性能
本文采用典型的优化算法测试函数测试IDE算法性能, 这里标准DE的R值设为0.2, F值设为0.5。而IDE算法中的F和R分别按照(6)~(7)式进行自适应变化, 且变异策略也按照(8)式进行, 选择和替换操作按照改进方案进行。为避免实验偶然性, 保证测试质量, 算法独立运行20次, 算法迭代次数为500, 种群大小为100, 维数为10。结果如表 1所示。
平均最优适应值用于衡量被测算法求解精度的优劣。平均最优适应值值越小, 求解精度越高。标准差用于衡量算法稳定性, 标准差值越小被测算法的稳定性越高。迭代相同次数的最优解越小, 代表算法的收敛速度更快。表 1通过对比这3个值可以看出IDE算法相较于标准DE算法求解精度高, 稳定性更好, 观察最优解对比发现IDE算法求得的解也更接近理论最优解, 收敛速度更快, 跳出局部最优解的能力更强。
算法寻优测试结果
2.2 基于IDE的SVM算法性能
实验数据选自UCI机器学习标准库中数据集。该数据集对应的任务是典型的二分类任务。由于SVM算法计算代价较大, 为了能够快速测试, 选取数据集中500组样例。实验数据选取不平衡会而影响分类结果, 因此实验选取的2类样本数接近。实验样本中, 70%作为训练样本, 30%作为测试样本, 核函数采用高斯核函数。
首先对DE算法中的参数进行初始化设置: 最大进化代数G=500, 种群规模N=80, 缩放因子k和交叉概率R按改进的自适应方案设置, 方差阈值τ=1, M=5, k=8。SVM惩罚参数C以及高斯核函数参数g的取值范围均设置为[0.000 1, 1 000]。误判率函数即适应度函数中a=3。实验结果如表 2所示。
从表 2可以看出, 与标准SVM算法模型相比, IDE-SVM算法模型, 分类精度更高, 分类结果更准确。
算法实验结果对比
2.3 物理层安全仿真分析
仿真实验假设合法无线终端与基站相距300 m且处于低速移动状态, 非法信号源以同样的频段模拟合法无线终端与基站进行通信。基站侧对接收信号的每个子帧进行15次均匀采样并提取对应的物理层特征得到信道特征向量。合法无线终端样本标签为1, 非法信号样本标签为-1。信道使用互耦信道模型, 基站采用线性天线阵列, 信道的信噪比为15 dB, 依据在非视距场景下到达时间差(TDOA)和到达角(AOA)的误差模型[15], 分别取合法无线终端TDOA分布区间U(1 μs, 1.3 μs), AOA分布区间U(0.1π, 0.15π), 取非法干扰信号源TDOA分布区间U(1.5 μs, 1.6 μs), AOA分布区间U(0.3π, 0.35π), 与基站相距200 m, 通信系统其他基本参数如表 3所示。
为防止因实验数据选取不平衡而导致分类结果影响, 样本集共有200个, 2类数据样本数接近, 仿真实验结果如图 2~3所示。
图 2a)是SVM参数选择优化前训练集的鉴权情况, 从图中可以看出基于标准SVM的安全接入认证模型有4个样本出现了错误判定。
图 2b)是SVM参数选择优化前基于训练集的参数选择结果与认证准确率, 其中g和C是SVM 2个参数的选择结果, 每组参数组合都对应着曲面上的一个接入认证准确率, 从图中可以看出参数选择优化前安全接入认证模型基于训练集的漏警率(即假设H1成立的条件下仍判别为来自合法无线终端)约2.9%。
图 2c)是SVM参数选择优化前测试集的鉴权情况, 从图中可以看出基于标准SVM的安全接入认证模型有2个样本出现了错误判定, 漏警率达到3.4%, 认证性能不佳。
图 3a)是SVM参数选择优化后训练集的鉴权情况, 图 3b)是SVM参数选择优化后基于训练集的参数选择结果与认证准确率, 从图中可以看出参数选择优化后安全接入认证模型基于训练集没有样本出现错误判定, 漏警率0.0%。
图 3c)是SVM参数选择优化后测试集的鉴权情况, 从图中可以看出IDE算法的安全接入认证模型预测结果与现实数据全都一致, 收获的认证精准率可达100%。
系统基本参数表
 |
图2 参数选择优化前实验结果图 |
 |
图3 参数优化后实验结果图 |
3 结论
本文主要研究了一种基于物联网物理层信息安全中的应用认证的IDE-SVM方案, 这种方案直接利用了通信过程中的信道物理层信息进行安全接入鉴权, 避免了使用复杂的通信上层协议进行加密解密和身份认证, 降低系统资源的开销和针对上层协议的接入认证攻击, 为无线通信终端安全接入问题提供了一种新的解决方案。IDE-SVM算法为参数寻优问题提供了一种新的参数寻优方案, 通过实验分析证明了此方案提高了算法分类精度和参数搜索的速度, 进一步提高了无线终端鉴权的准确性。
References
- ISHAQ M, AFZAL M H, TAHIR S, et al. A compact study of recent trends of challenges and opportunities in integrating internet of things(IOT) and cloud computing[C]//2021 International Conference on Computing, Electronic and Electrical Engineering, 2021: 1–4 [Google Scholar]
- CHEN Z, LI J, LI J, et al. GNSS multiparameter spoofing detection method based on support vector machine[J]. IEEE Sensors Journal, 2022, 22(18): 17864–17874. [Article] [CrossRef] [Google Scholar]
- LIU Y, ZHANG P, LI X. Physical layer authentication using mmwave channel state information[C]//2021 International Conference on Networking and Network Applications, 2021: 30–33 [Google Scholar]
- AFEEF L, FURQAN H M, ARSLAN H. Physical layer authentication scheme in beamspace MIMO systems[J]. IEEE Communications Letters, 2022, 26(7): 1484–1488. [Article] [CrossRef] [Google Scholar]
- FODOR G, PARKVALL S, SORRENTINO S, et al. Device-to-device communications for national security and public safety[J]. IEEE Access, 2014, 2: 1510–1520. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- VAPNIK V N. An overview of statistical learning theory[J]. IEEE Trans on Neural Networks, 1999, 10(5): 988–999. [Article] [CrossRef] [Google Scholar]
- KAZEMI A, BOOSTANI R, ODEH M, et al. Two-layer SVM, towards deep statistical learning[C]//2022 International Engineering Conference on Electrical, Energy, and Artificial Intelligence, 2022: 1–6 [Google Scholar]
- YIN T, LI Y, FAN J, et al. A novel gated recurrent unit network based on svm and moth-flame optimization algorithm for behavior decision-making of autonomous vehicles[J]. IEEE Access, 2021, 9: 20410–20422. [Article] [CrossRef] [Google Scholar]
- GASCÓN-MORENO J, SALCEDO-SANZ S, ORTIZ-GARCÍA E G, et al. A binary-encoded tabu-list genetic algorithm for fast support vector regression hyper-parameters tuning[C]//Proceedings of the 2011 11th International Conference on Intelligent Systems Design and Applications, 2011: 1253–1257 [Google Scholar]
- CHEN C, XU X, WANG G, et al. Network intrusion detection model based on neural network feature extraction and PSO-SVM[C]//2022 7th International Conference on Intelligent Computing and Signal Processing, 2022: 1462–1465 [Google Scholar]
- WANG Z, JIANG Y, HU X, et al. A leaf type recognition algorithm based on SVM optimized by improved grid search method[C]//2020 5th International Conference on Electromechanical Control Technology and Transportation, 2020: 312–316 [Google Scholar]
- LI J, DING L, XING Y. Differential evolution based parameters selection for support vector machine[C]//2013 Ninth International Conference on Computational Intelligence and Security, 2013: 284–288 [Google Scholar]
- CHENG Y, LIU Z. Passive oppositional differential evolution for global optimization[C]//2019 11th International Conference on Intelligent Human-Machine Systems and Cybernetics, 2019: 323–327 [Google Scholar]
- WANG P, YAN Z, ZENG K. Bcauth: physical layer enhanced authentication and attack tracing for backscatter communications[J]. IEEE Trans on Information Forensics and Security, 2022, 17: 2818–2834. [Article] [CrossRef] [Google Scholar]
- DAI C, YANG J, QIN Y, et al. Physical layer authentication algorithm based on SVM[C]//2016 2nd IEEE International Conference on Computer and Communications, 2016: 1597–1601 [Google Scholar]
All Tables
All Figures
|
图1 无线终端安全接入方法流程图 |
| In the text | |
|
图2 参数选择优化前实验结果图 |
| In the text | |
|
图3 参数优化后实验结果图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.