EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 42 / No 5 (October 2024) JNWPU, 42 5 (2024) 948-958 Full HTML
Open Access
Issue
JNWPU
Volume 42, Number 5, October 2024
Page(s) 948 - 958
DOI https://doi.org/10.1051/jnwpu/20244250948
Published online 06 December 2024

© 2024 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

优化问题长期以来一直是一个基础研究课题, 其在农业生产管理、军事指挥运筹、大规模复杂性网络、资源分配、任务分配等领域中都有着巨大的应用潜力, 吸引了广泛的探讨和研究[1–5]。进化算法是高效求解复杂优化问题最常用的一类算法, 包括遗传算法[6]、禁忌搜索[7]和模拟退化[8]等, 其中, 粒子群优化(particle swarm optimization, PSO)算法凭借结构简单、收敛迅速、计算成本低以及通用性强等优点脱颖而出[9–10]。

PSO算法是于1995年由Kenny和Eberhart受到人工生命结果的启发，通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法[11]。与其他进化算法相类似, PSO算法基本思想也是基于“种群”和“进化”的生物社会背景概念, 粒子运动源于个体之间的协作与竞争活动的规律性, 利用种群中信息的社会共享产生从无序到有序的演化运动, 实现在复杂空间对最优解的搜索[12–13]。目前已经被广泛应用于多种类型问题的求解, 如高维度优化问题、多模优化问题、多目标优化问题和离散超空间优化问题等, 在资源管理、电力系统等领域也被广泛应用[14]。

同时PSO算法也有着不可忽视的缺陷和不足[15]。一方面是难以平衡粒子多样性和算法收敛速度, 使得群体演化过程容易陷入局部最优; 另一方面, 粒子仅认知学习粒子最优和种群最优的位置信息进行更新, 而忽略了其他有效信息, 导致搜索策略执行效率低下。实际上, PSO算法的收敛速度及精度与搜索策略和相应的控制参数等因素密切相关[16]。针对以上问题, 诸多学者对PSO算法进行了优化和改进, 相关研究可以概括为四方面: 控制参数、种群拓扑结构、学习策略和融合算法。

1) PSO算法惯性权重和加速度系数等控制参数的自适应调整

文献[17]向原始粒子群算法中引入了随时间递减的惯性权重系数, 大大提高了粒子群算法的性能, 一定程度上实现了粒子进化中搜索和开发之间的平衡。文献[18]定义了一个PSO算法的广义模型, 该模型采用带有压缩系数的随机系数, 有效提升了算法的收敛度。文献[9]定义了自适应粒子群优化(adaptive particle swarm optimization, APSO)算法实时框架下粒子进化的搜索、开发、收敛和跳出4种状态, 并据此实现了对惯性权值和加速度系数等算法参数的自适应控制, 增强了算法的局部搜索能力。文献[19]引入了时变加速度系数, 在避免搜索前期早熟收敛的同时提高了优化末尾的收敛精度。文献[20]提出了一种基于sigmoid函数的加权策略来自适应调整加速度系数, 在其中同时考虑了粒子全局最佳位置和到自身最佳位置的距离, 最终显著提升了收敛速度。

2) PSO算法中粒子分布邻域拓扑结构的改进

种群拓扑结构的设计对于算法性能有着关键作用, 例如全连接结构、环形结构等各种拓扑结构均有不同的影响[21]。文献[22]采用一种综合学习策略, 粒子的每个维度独立地选择范例学习, 更加有效地利用种群信息, 显著提高了PSO的性能。文献[23]将动态学习策略分为普通粒子的开发行为和通信粒子的探索行为, 促进粒子之间的信息交换。文献[24]依据粒子间距离信息动态调整粒子个体邻域, 并结合切换学习策略以便充分利用整个蜂群的种群演化信息。

3) PSO算法中粒子进化学习策略的开发

文献[22]提出一种采用综合学习策略的变体PSO算法, 进化粒子使用所有其他粒子的历史最佳信息更新粒子的速度, 保留了种群的多样性, 避免了早熟收敛。文献[25]将动物世界中的社会学习机制引入到粒子群算法中, 赋予粒子向任意示范粒子学习的能力, 提升了算法的搜索效率。文献[26]采用了一种动态分段的混合学习策略, 分别利用基于动态分段的均值学习策略(DSMLS)和多维综合学习策略(MDCLS)实现种群协同进化和收敛速度精度的提升。

4) PSO算法与其他优化技术的交叉融合

人们尝试将PSO算法与其他算法相结合而形成一种性能更为优异的混合粒子群算法[27]。例如, 遗传算法改进的粒子群(PSO-genetic algorithm, PSO-GA)算法[28]、遗传算法改进的粒子群算法(PSO-simulated annealing, PSO-SA)算法[29]、差分进化算法改进的粒子群(PSO-differential evolution, PSO-DE)算法[29]等。除此之外, 文献[10]提出了基于小生境技术的粒子群优化算法, 提高了粒子群算法求解多峰优化问题的能力; 文献[30]结合混沌运动遍历性改善了粒子优化算法容易陷入局部极值的问题, 提高了算法的收敛精度和速度; 文献[31]专门在粒子群算法中引入局部搜索策略, 实现了在局部最优位置对潜在较优解的搜索, 打破了粒子在局部最优的停滞, 并增加了收敛速度。

总而言之, 以上4种PSO的改进方式都是通过改变种群迭代方式或者增强算法的种群多样性, 从而强化算法的全局搜索能力、缓解早熟的问题, 最终提高算法的收敛性能。虽然现有的粒子群优化算法改进研究主要集中于状态初始化、种群进化拓扑或粒子更新机制等单一环节的改进设计, 但这些改进算法在某些环节中仍然存在优化瓶颈。因此, 为了提高优化效果, 需要从整体上协调粒子进化的各个环节, 并设计基于粒子进化全环节的改进技术。

为此, 同时从以上总结的4个改进角度出发, 提出一种新的分层组织的精英引导社会学习粒子群优化算法(elite guidance-based social learning particle swarm optimization, ESLPSO)。首先依据粒子适应度表现动态划分精英粒子和平民粒子改进算法的拓扑结构, 为不同粒子分配定制调优方法, 使粒子在应对复杂情况时发挥不同的作用。同时引入社会学习机制拓展种群演化过程中的多维信息, 并基于精英粒子引导的种群集体经验驱动平民粒子生成更加有潜力的子代粒子。利用多维种群信息改善了基本PSO算法对于种群最优和全局最优粒子的过度依赖。此外, 为平衡种群在搜索过程中的探索和开发能力, 在算法中融合扰动操作, 在平民粒子社会学习策略中增加极值扰动机制赋予子代粒子态叠加的不确定性, 以平衡种群的搜索和开发能力。

1 粒子群算法模型

1.1 经典粒子群算法

粒子群优化算法是一种基于迭代的全局随机搜索算法, 它将问题的若干个潜在解抽象为粒子, 通过群体在搜索空间的飞行行为模拟迭代优化问题。粒子种群规模为N, 每个粒子代表D维搜索空间中的一个潜在解决方案。第t次迭代中第i个粒子的位置矢量和速度矢量分别表示为Xit=(Xi, 1t, Xi, 2t, …, Xi, Dt)与Vit=(Vi, 1t, Vi, 2t, …, Vi, Dt)。在群体进化过程中, 粒子群算法会不断生成和更新第i个粒子的最佳历史位置pbest, it=(pbest, i, 1t, pbest, i, 2t, …, pbest, i, D)t, 以及群体最优位置gbestt=(gbest, 1t, gbest, 2t, …, gbest, Dt)。经典粒子群算法中粒子位置与速度的更新策略为

式中, 惯性权重系数ω决定粒子对上一次速度的继承比例; c1和c2分别为自身加速常数和社会加速常数, 影响粒子在搜索空间内局部或者全局影响的比重, c1控制自我认知部分, 体现粒子向该粒子的历史最佳位置飞行动作，c2控制社会认知部分, 指导粒子与种群之间的信息; u1t和u2t是均匀分布在[0, 1]之间的随机数。为每个粒子确定的速度值设置速度限制[Vmax, Vmin]以防止粒子急剧变化。

显然, 在经典粒子群架构下粒子进化迭代分别是由原始惯性速度、粒子自我认知记忆以及种群社会的信息交互三部分共同控制, 拥有结构简单、求解快捷的优点, 在处理复杂优化问题上具有一定的优势。但PSO算法结构单一且参数固定, 在优化后期粒子飞行速度容易急剧降低, 导致收敛速度变慢, 产生早熟收敛和难以摆脱局部极值的问题。

1.2 典型的PSO改进算法

本文选择2个典型的PSO变体作为介绍, 这些PSO变体启发了本文提出的算法。

1) 综合学习粒子群优化器(comprehensive learning particle swarm optimizer, CLPSO)

CLPSO通过使用所有其他粒子的历史最佳信息更新粒子的速度以维持种群的多样性, 避免早熟收敛问题[22]。该学习策略中使用了以下速度更新方程

式中，ω, c, u1t+1与基本粒子群算法中的定义一致。不同的是, CLPSO将粒子学习对象扩大到整个种群, 粒子将根据其随机数与学习概率决定粒子学习。

该算法将粒子学习对象的范围扩大到整个种群, 范例粒子的最佳历史位置信息更加全面地反映了整个种群, 为保持种群多样性提供强有力的保障。但是, 其舍弃了全局最优粒子这一维关键信息, 导致收敛速度和搜索精度具有局限性。

2) 自调节自进化粒子群优化器(self-regulating and self-evolving particle swarm optimizer, SRPSO)

文献[32]提出一种自调节自进化的粒子位置更新策略以加快收敛速度、增加多样性和防止过早收敛。当搜索过程中粒子的pbest, it未能提高时, 结合反转思想赋予粒子一个反向速度更新位置

式中: c3为控制粒子飞行的正常数; R3为对角元素随机分布于[0, 1]的D×D矩阵。在此基础上, 结合自进化行为突变操作生成新的全局最优粒子。粒子最优位置和全局最优位置均采用贪婪更新思想, 分别对一般粒子和全局最优粒子的更新进行改进, 所提出的这种分层处理机制有效提升了算法的收敛性能和可靠性。

2 基于精英引导的社会学习PSO算法

2.1 Cubic立方混沌初始化

种群初始粒子位置的散布程度及其在搜索空间中的均匀覆盖程度, 将直接影响整个算法的收敛速度和寻优效率[20]。在面向大范围搜索空间和小样本粒子种群时随机初始化策略表现较为乏力, 相较而言, 混沌强烈的无规则非线性运动具有良好的遍历性和随机性[33]。因此, 本文利用图 1中均匀性更好的Cubic混沌映射赋予粒子无规则非线性运动状态, 有效保证了初始化粒子位置的随机程度, 提高了粒子初始化在解空间内的均匀覆盖程度, 提升了算法初始阶段的搜索效率[34]。具体而言, Cubic立方混沌映射公式为

式中, ρ为混沌控制参数, 所产生的变量值yi=(yi, 1, yi, 2, …, yi, D)为随机在[-1, 1]D内生成的D维向量。当ρ=2.595, y0=0.3时, Cubic映射具有较好的混沌遍历性, 具备在一定范围内对所有状态不重复遍历的能力。在此基础上, 将Cubic映射产生的变量值映射到种群个体并作为初始粒子位置

式中，Xub与Xlb表示粒子初始化的上界和下界。

thumbnail 图1

Cubic混沌映射示意图

2.2 精英引导的社会学习机制

如前所述, 传统的粒子群优化算法进化机制仅利用单个粒子的pbest和全局种群的gbest进行平行四边形矢量加法运算来更新每个粒子, 不能有效利用其他更有前途的粒子或者种群有效信息来提高进化效果和缓解早熟收敛问题[35]。针对这一缺陷, 本文引入一种精英粒子引导的社会学习机制, 在向适应度占优的粒子学习的同时, 把整个群体的演化信息也拓展为粒子学习部分, 更加全面地利用了粒子进化信息。

首先, 为了提高群体算法高效优化求解的鲁棒性, 兼顾单模态优化问题和复杂密集的多模态优化问题下算法种群规模的合理设置, 保证在问题维数较高的情况下相应扩大种群规模[36], 将生成种群的大小设置成为关于搜索维度的函数, 表示为

式中：M为基本种群规模；D为初始种群的维数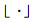；为下取整函数。由初始粒子计算适应度值, 并在此基础上粒子进行排序和进化学习运动。

按照粒子适应度表现对粒子从劣到优排序以区分精英粒子与平民粒子, 并根据粒子表现设定学习概率赋予粒子不同的学习意愿。具体而言, 适应度表现越好的粒子向其他较优粒子学习的能力越弱。另外, 为了保证粒子在应对高维度、变量耦合的优化问题时保持更好的多样性, 需要使得问题维度升高时粒子学习意愿降低。因此, 粒子采用以下概率学习进化

式中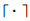，为上取整函数，常数ϕ＜1与log2(·)函数用于平滑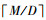。显然, 粒子学习概率与粒子排序编号呈反比, 适应度越优粒子的社会学习能力越弱; 当处理大规模高维复杂问题时, 减小粒子学习以保持更好的种群多样性。

在更新机制中, 每一个粒子都要向优质的示范体粒子学习, 但粒子学习的方向只能是趋于提升种群的适应度表现。为赋予粒子学习机制的随机性, 随机学习概率Pi(t)∈(0, 1)位于区间[0, PiL]时才采用社会学习策略更新粒子[25]。

式中, ΔXi, jt+1为学习偏移量定义为

式中，收缩因子r1t, r2t和r3t为每一次迭代中产生的[0, 1]范围内的随机数, ε=η×D/M为集体行为学习因子; η为学习率, 按照经验取值为0.01时在各维度下算法能取得较好收敛效果。其中Ii, jt和Wi, jt具体为：

式中, Cjt为当前种群中所有粒子第j维的平均位置, 更广泛地利用了样本集合提供的种群集体信息; k∈(i, N]表示种群中相对于第i个粒子的较优粒子。

如图 2所示，更新后的粒子位置的决定因素可以划分为三部分: 粒子历史经验Xi, jt、精英粒子k的学习行为Xk, jt、种群集体行为ε·Wi, j(t)。ΔXi, jt与规范粒子群中的惯性分量类似, 传递粒子的历史经验信息; 精英粒子引导的学习行为打破了大多数粒子群单一学习群体最优个体的局限性, 使得粒子每一维度随机学习当前种群中的范例(Xk, jt, 其中i≤k＜m), 避免过度依赖于当前种群的最优粒子, 有效增强了粒子进化的多样性; 此外, 种群的平均行为对所有粒子诱发群体级的从众现象, 将Cjt作为种群集散度的反映从而更加全面地挖掘种群信息, 有效缓解早熟收敛的问题。

综上所述, 在自适应调整种群规模的基础上, 通过图 2中的循环机制, 更好利用了种群学习的有效信息, 增加了粒子进化进程中状态迭加的不稳定性, 以达到算法收敛和粒子多样性之间的良好平衡, 能够在不需要额外微调参数的情况下稳健地执行各种搜索维度尺寸的问题。

thumbnail 图2

精英粒子引导的社会学习机制

2.3 极值扰动因子

实验表明, 种群中的粒子在进化进程时会停滞在粒子极值本身或者种群极值处, 在高密度的搜索飞行之后难以突破局部极值, 往往导致粒子陷入局部最优影响最终的优化求解效率[37–38]。然而单纯增加种群样本数量仍然难以打破饱和限制, 需要从搜索方式上摆脱粒子聚集到自身极值和群体全局极值决定的极值停滞点, 增强粒子的进化潜力。

为此, 在粒子搜索飞行进化过程中添加迁移机制激励粒子经历新的搜索路径和区域, 通过随机扰动来摆脱在局部极值的停滞局面, 降低早熟收敛现象发生的概率[18], 从而再次恢复种群的多样性、增强种群的可进化潜力。本文将粒子在当前最优位置的进化停滞步数t作为极值扰动触发条件, 同时对pbest, i, jt与gbest, jt进行随机扰动, 并在学习偏移量中补充极值扰动算子。Ii, jt和Wi, jt增加极值扰动算子后的具体形式为

式中：te与tm分别表示精英粒子和群体学习行为的进化停滞步数；Te与Tm分别为精英粒子和群体学习行为增加扰动的进化停滞步数阈值。r4te>Te与r5tm>Tm分别表示带条件的U(0, 1)分布的随机函数, 有

由于均匀随机函数r4和r5的影响, 演化过程中各学习分量的长度略有变化。

3 实验验证与对比分析

为了充分验证ESLPSO算法的优化性能和稳定性, 将该算法与一些先进的PSO改进算法在基准函数测试集上进行了一系列比较。文中所有仿真实验均在Interl Core i7 2.60 GHz CPU, 7 GB运行内存的64位Windows 10的计算机上运行, 并使用Matlab 2019a软件进行实验验证。为消除随机影响, 所有实验结果均为30次独立重复运行后的平均值。

3.1 基准函数和对比算法

表 1中总结了本文用于算法测试的12个基准函数, 涵盖了许多不同类型的问题。表 2中给出了基准测试函数, 包括函数名称、搜索空间和范围、特征。其中单峰函数(U)只有一个局部最优或者一个全局最优, 常被用来测试粒子进化的开发能力; 多峰函数(M)与多峰旋转函数(R)容易使探索性能乏力的算法陷入局部最优。所有算法运行的终止条件均为最大评价次数(MaxFEs)。

最后, 文中选取了其他7种PSO算法与本文方法进行性能比较, 具体的算法来源和参数设置如表 2所示。

仿真实验中所有的基准函数的种群大小M均为100, 搜索空间的维度D为30。每次运行的最大函数计算次数(MaxFEs)最大迭代次数为5 000。

表1

基准函数测试集

表2

8种算法的参数设置

3.2 求解精度比较及分析

为了全面评估所提出的ESLPSO的收敛精度, 表 3给出了所有算法在基准函数上运行30次后的平均值(mean)、最优解(beat value)和标准差(Std. Dev.)的信息, 并粗体显示最优的结果数值。其中标准差反映了结果之间的不一致性程度, 可以通过检查标准差来衡量算法搜索的稳健性[20]。

从表 3可以看出, 本文算法针对除f3外所有测试函数的搜索精度都优于其他算法, 表现出了最好的性能。无论是针对单峰函数还是多峰函数, ESLPSO函数搜索结果的均值与标准差显示ESLPSO具有更加优秀的搜索精度和稳定性。对于单峰函数而言, ESLPSO优于以往优化算法数十倍。面对多峰函数时, ESLPSO大幅提升搜索结果精度, 甚至得到精确最优解。同时, 所提算法在解决多峰旋转问题时也展现出显著优势。总而言之, 本文所提出的改进方法可以有效提高算法收敛精度与搜索结果的稳健程度。

表3

运行结果对比

3.3 收敛性能比较分析

虽然DNSPSO在f3与f11上表现出了出色的性能, 但ESLPSO也仅次于他收敛到最优值, 并且其优势并不显著。观察图 3d), 面对搜索空间极大、峰值极多且分布极不规则的Schwefel 2.26测试函数, 并且这个函数的各个局部优解的差值极小、寻优难度较大, 所有算法均陷入了局部最优, 但ESLPSO的在收敛速度和求解精度方面的优势突出。

为了更加直观地对比不同算法在精度上的差别以及迭代速度, 图 3种绘制了30维下算法对各基准函数的收敛曲线。其中纵坐标为指数形式的平均适应度值, 横坐标为迭代次数。从图中可以看到, ESLPSO算法在大多数基准函数上表现出具有竞争力的性能。尤其是面对简单的单峰函数, ESLPSO算法的收敛更快、具有更令人满意的平均适应度值。

如图 3e)~3j)所示, 大部分算法在迭代中期都陷入局部最优, 跳出局部最优解的能力随搜索进程衰减。但本文所提出的ESLPSO算法融合了扰动算子，增加了状态迭加的不确定性, 驱动种群逃脱了局部极小值, 从而更接近最优结果, 获得了更高效和成功的结果。综上所述, 所提ESLPSO算法在收敛速度上也具有一定的优势。

thumbnail 图3

算法收敛性表现

3.4 种群多样性比较分析

探索和开发能力的协调决定了算法的全局搜索性能, 对粒子在进化进程中种群多样性变化的分析将更深层次地反映算法中粒子搜索时的收敛状态。种群多样性度量可计算为

式中，Xjt在第t次迭代第j维对所有粒子的平均值, 也即 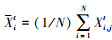。多样性曲线走势实质上反映了种群的搜索状态的变化, 反映出种群演化进程中开发、探测、收敛和跳出4个基本种群状态。本文提出的ELSPSO和其他6种PSO变体的种群多样性如图 4所示, 其中纵坐标以指数形式表示蜂群的多样性度量, 横坐标表示迭代次数。

由图 4可以看出, ESLPSO算法和其他PSO算法在优化过程前期都具有较大的种群多样性值。如图 4a)~4b)所示, 随着算法搜索进程的不断推进, 所有算法的种群多样性都随着迭代有不同程度收敛。

虽然BreedPSO, AWSPO以及DNSPSO算法的多样性曲线也有类似的起伏现象, 但是其本质上都期望通过种群多样性调整提升算法的全局搜索能力。对于所提出的ESLPSO算法, 正是由于扰动机制和学习机制的持续作用使得ELSPSO在整个收敛进程中多样性曲线呈现出显著的波动特性, 在探索和开发之间达成较好的折中。

从图 4e)~4g)与图 4k), 图 4l)可以看出, 当种群搜索到最优值时, 多样性下降到并保持在一定数值水平时, 扰动机制使得种群在收敛到最优值时仍然具备一定水平的多样性程度。尤其是在图 4h)及图 4i)中, 算法陷入到局部最优而搜索停滞的情况下, ESLPSO实现了对种群多样性的调整, 种群多样性跳跃攀升到一定水平以维持种群的探索能力, 赋予了种群跳出局部最优的能力和更好的求解精度。

统筹分析图 3~4, 当基准算法由于早期收敛而陷入局部极小值时, ESLPSO算法总能逃脱局部极小值, 并逼近多模态函数的最优解。特别是本文所提算法与SLPSO算法测试结果表明，本文设计的耦合分层机制能够有效提升算法的优化求解性能。因此, 可以得出结论, 提出的ESLPSO算法在种群多样性表现上仍然具有一定有优势。

thumbnail 图4

算法种群多样性表现

4 结论

本文提出了ESLPSO算法, 以期提高经典粒子群优化算法的搜索能力。在ESLPSO中, 群体首先通过Cubic混沌初始化提高初始粒子在搜索空间的均匀覆盖程度。并将种群按照适应度值表现重新构造为具有分层拓扑结构的粒子组织, 并引入一种新颖的种群进化机制。

首先, 将适应度表现较优的粒子作为种群精英粒子, 其余粒子则作为平民粒子。平民粒子采用精英引导的社会学习机制以加强群体引导, 改良了粒子最优状态和全局粒子最优状态引导的局限性。在此基础上引入极值扰动因子, 增加平民粒子态叠加的不确定性, 改善了最优粒子滞塞于局部最优的现象, 丰富了种群的多样性。为了验证ESLPSO算法的有效性, 本文利用了12个常用的优化基准函数(包括单峰, 无旋转多峰和旋转多峰函数)对8个PSO改进算法分别进行了求解精度、收敛分析以及种群多样性分析。实验结果表明: ESLPSO显著提高了PSO的性能, 并在大多数优化问题上给出了最好的性能, 在提高问题求解精度和收敛速度方面具有一定的竞争力, 特别是在复杂的多模态函数上, 具有出色的综合性能。

未来的目标是进一步提高ESLPSO算法的收敛速度和求解精度。此外将着重把所提算法应用在自组织RBF神经网络[40]、系统工程[41–42]和信号处理[43–44]等更复杂的实际优化问题中。

References

  1. SHEN C, ZHANG K. Two-stage improved grey wolf optimization algorithm for feature selection on high-dimensional classification[J]. Complex & Intelligent Systems, 2021, 8(4): 2769–2789 [Google Scholar]
  2. OU X F, WU M, PU Y Y, et al. Cuckoo search algorithm with fuzzy logic and Gauss-Cauchy for minimizing localization error of WSN[J]. Applied Soft Computing, 2022, 125: 109211. [Article] [CrossRef] [Google Scholar]
  3. MONTALVO I, IZQUIERDO J, PÉREZ R, et al. A diversity-enriched variant of discrete PSO applied to the design of water distribution networks[J]. Engineering Optimization, 2008, 40(7): 655–668. [Article] [CrossRef] [Google Scholar]
  4. GONG Y J, ZHANG J, CHUNG S H, et al. An efficient resource allocation scheme using particle swarm optimization[J]. IEEE Trans on Evolutionary Computation, 2012, 16(6): 801–816. [Article] [CrossRef] [Google Scholar]
  5. ZHANG H, XIE J, GE J, et al. An entropy-based PSO for DAR task scheduling problem[J]. Applied Soft Computing, 2018, 73: 862–873. [Article] [CrossRef] [Google Scholar]
  6. GOLDBERG D E. Genetic algorithms in search, optimization, and machine learning[M]. Boston: Adottion-Wesley Professional, 1989 [Google Scholar]
  7. YANG J, YANG S, NI P. A vector tabu search algorithm with enhanced searching ability for pareto solutions and its application to multi-objective optimizations[J]. IEEE Trans on Magnetics, 2016, 52(3): 1–4 [NASA ADS] [Google Scholar]
  8. MARTINS D, MENDES M. A Hybrid evolutionary approach applied to the economic dispatch problem with prohibited operating zones and uncertainties[J]. Latin America Transactions, 2021, 19(7): 1225–1232. [Article] [CrossRef] [Google Scholar]
  9. ZHAN Z H, ZHANG J, YUN L, et al. Adaptive particle swarm optimization[J]. IEEE Trans on Systems, Man, and Cybernetics, Part B: Cybernetics, 2009, 39(6): 1362–1381. [Article] [CrossRef] [Google Scholar]
  10. LIU Q, DU S, WYK B J V, et al. Niching particle swarm optimization based on euclidean distance and hierarchical clustering for multimodal optimization[J]. Nonlinear Dynamics, 2020, 99(1): 1–19. [Article] [CrossRef] [Google Scholar]
  11. KENNEDY J, EBERHART R. Particle swarm otimization[C]//International Conference on Neural Networks, 1995 [Google Scholar]
  12. EBERHART R, KENNEDY J. A new optimizer using particle swarm theory[C]//Proceedings of the Sixth International Symposium on Micro Machine and Human Science, 1995: 39–43 [Google Scholar]
  13. SHI Y. Parameter selection in particle swarm optimization[J]. Evolutionary Programming, 1998, 1447: 591–600 [CrossRef] [Google Scholar]
  14. CAO Y, ZHANG H, LI W, et al. Comprehensive learning particle swarm optimization algorithm with local search for multimodal functions[J]. IEEE Trans on Evolutionary Computation, 2019, 23(4): 718–731. [Article] [CrossRef] [Google Scholar]
  15. YU W, LI B, WEISE T, et al. Self-adaptive learning based particle swarm optimization[J]. Information Sciences, 2011, 181(20): 4515–4538. [Article] [CrossRef] [Google Scholar]
  16. YU F, TONG L, XIA X W. Adjustable driving force based particle swarm optimization algorithm[J]. Information Sciences, 2022, 609: 60–78. [Article] [CrossRef] [Google Scholar]
  17. SHI Y, EBERHART R. A modified particle swarm optimizer[C]//1998 IEEE International Conference on Evolutionary Computation, 1998: 69–73 [Google Scholar]
  18. CLERC M, KENNEDY J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J]. IEEE Trans on Evolutionary Computation, 2002, 6(1): 58–73. [Article] [CrossRef] [Google Scholar]
  19. RATNAWEERA A, HALGAMUGE S K, WATSON H C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients[J]. IEEE Trans on Evolutionary Computation, 2004, 8(3): 240–255. [Article] [CrossRef] [Google Scholar]
  20. LIU W, WANG Z, YUAN Y, et al. A novel sigmoid-function-based adaptive weighted particle swarm optimizer[J]. IEEE Trans on Cybernetics, 2021, 51(2): 1085–1093. [Article] [CrossRef] [Google Scholar]
  21. RUI M, KENNEDY J, NEVES J. The fully informed particle swarm: simpler, maybe better[J]. IEEE Trans on Evolutionary Computation, 2004, 8(3): 204–210. [Article] [CrossRef] [Google Scholar]
  22. LIANG J J, QIN A K, SUGANTHAN P N, et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J]. IEEE Trans on Evolutionary Computation, 2006, 10(3): 281–295. [Article] [CrossRef] [Google Scholar]
  23. YE W, FENG W, FAN S. A novel multi-swarm particle swarm optimization with dynamic learning strategy[J]. Applied Soft Computing, 2017, 61: 832–843. [Article] [CrossRef] [Google Scholar]
  24. ZENG N Y, WANG Z D, LIU W B, et al. A dynamic neighborhood-based switching particle swarm optimization algorithm[J]. IEEE Trans on Cybernetics, 2020, 50(1): 1–12. [Article] [Google Scholar]
  25. CHENG R, JIN Y. A social learning particle swarm optimization algorithm for scalable optimization[J]. Information Sciences, 2015, 291: 43–60. [Article] [CrossRef] [Google Scholar]
  26. LI W, MENG X, HUANG Y, et al. Multi-population cooperative particle swarm optimization with a mixed mutation strategy[J]. Information Sciences, 2020, 529: 179–196. [Article] [CrossRef] [Google Scholar]
  27. HUANG Yi, LIANG Fangchi, FAN Chengli, et al. Particle swarm optimization algorithm with random mutation and perception factor[J]. Journal of Northwestern Polytechnical University, 2023, 41(2): 428–438 (in Chinese) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. KUMAR N, VIDYARTHI D P. A novel hybrid PSO-GA meta-heuristic for scheduling of DAG with communication on multiprocessor systems[J]. Engineering with Computers, 2016, 32(1): 35–47. [Article] [CrossRef] [Google Scholar]
  29. JAVIDRAD F, NAZARI M. A new hybrid particle swarm and simulated annealing stochastic optimization method[J]. Applied Soft Computing, 2017, 60: 634–654. [Article] [CrossRef] [Google Scholar]
  30. THARWAT A, ELHOSENY M, HASSANIEN A E, et al. Intelligent Bézier curve-based path planning model using chaotic particle swarm optimization algorithm[J]. Cluster Computing, 2019, 22(4): 1–22 [CrossRef] [Google Scholar]
  31. ZHANG R, CHANG P C, SONG S, et al. Local search enhanced multi-objective PSO algorithm for scheduling textile production processes with environmental considerations[J]. Applied Soft Computing, 2017, 61(1): 447–467 [CrossRef] [Google Scholar]
  32. WANG H M, QIAO Z W, XIA C L, et al. Self-regulating and self-evolving particle swarm optimizer[J]. Engineering Optimization, 2015, 47(1): 129–147. [Article] [CrossRef] [Google Scholar]
  33. JAMES F. Chaos and randomness[J]. Chaos Solitons & Fractals, 1995, 6: 221–226 [CrossRef] [Google Scholar]
  34. ZHANG M, LONG D, QIN T, et al. A chaotic hybrid butterfly optimization algorithm with particle swarm optimization for high-dimensional optimization problems[J]. Symmetry, 2020, 12(11): 1800 [CrossRef] [Google Scholar]
  35. XIA X W, GUI L, HE G L, et al. An expanded particle swarm optimization based on multi-exemplar and forgetting ability[J]. Information Sciences: an International Journal, 2020, 508: 105–120 [CrossRef] [Google Scholar]
  36. VESTERSTROM J, THOMSEN R. A comparative study of differential evolution, particle swarm optimization, and evolutionary algorithms on numerical benchmark problems[C]//Proceedings of the 2004 Congress on Evolutionary Computation, 2004: 1980–1987 [Google Scholar]
  37. YAN Qunmin, MA Ruiqing, MA Yongxiang, et al. Adaptive simulated annealing particle swarm optimization algorithm[J]. Journal of Xidian University, 2021, 48(4): 8 (in Chinese) [Google Scholar]
  38. LU Fuyu, TONG Ningning, FENG Weike, et al. Adaptive hybrid annealing particle swarm optimization algorithm[J]. Systems Engineering and Electronics, 2022, 44(11): 3470–3476 (in Chinese) [Google Scholar]
  39. JIANG J, LI X, DENG Z H, et al. Control-oriented dynamic model optimization of steam reformer with an improved optimization algorithm[J]. International Journal of Hydrogen Energy, 2013, 38(26): 11288–11302 [CrossRef] [Google Scholar]
  40. RAN C, JIN Y, et al. A social learning particle swarm optimization algorithm for scalable optimization[J]. Information Sciences an International Journal, 2015, 291: 43–60 [CrossRef] [Google Scholar]
  41. HAN H, WU X, ZHANG L, et al. Self-organizing RBF neural network using an adaptive gradient multiobjective particle swarm optimization[J]. IEEE Trans on Cybernetics, 2019, 49(1): 69–82 [CrossRef] [Google Scholar]
  42. LIU S, WANG Z, WEI G, et al. Distributed set-membership filtering for multi-rate systems under the round-robin scheduling over sensor networks[J]. IEEE Trans on Cybernetics, 2020, 50(5): 1910–1920 [CrossRef] [Google Scholar]
  43. ZOU, LEI, WANG, et al. Recursive filtering for time-varying systems with random access protocol[J]. IEEE Trans on Automatic Control, 2019, 64(2): 720–727 [Google Scholar]
  44. ZOU L, WANG Z, HAN Q L, et al. Moving horizon estimation for networked time-delay systems under round-robin protocol[J]. IEEE Trans on Automatic Control, 2019, 64(12): 5191–5198 [CrossRef] [Google Scholar]

All Tables

表1

基准函数测试集

In the text
表2

8种算法的参数设置

In the text
表3

运行结果对比

In the text

All Figures

thumbnail 图1

Cubic混沌映射示意图
In the text
thumbnail 图2

精英粒子引导的社会学习机制
In the text
thumbnail 图3

算法收敛性表现
In the text
thumbnail 图4

算法种群多样性表现
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.