| Issue |
JNWPU
Volume 41, Number 6, Decembre 2023
|
|
|---|---|---|
| Page(s) | 1170 - 1178 | |
| DOI | https://doi.org/10.1051/jnwpu/20234161170 | |
| Published online | 26 February 2024 | |
DE-JSMA: a sparse adversarial attack algorithm for SAR-ATR models
DE-JSMA: 面向SAR-ATR模型的稀疏对抗攻击算法
1
School of Cyberspace Security, Northwestern Polytechnical University, Xi'an 710072, China
2
School of Automation, Northwestern Polytechnical University, Xi'an 710072, China
Received:
27
December
2022
The vulnerability of DNN makes the SAR-ATR system that uses an intelligent algorithm for recognition also somewhat vulnerable. In order to verify the vulnerability, this paper proposes DE-JSMA, a novel sparse adversarial attack algorithm based on a salient map's adversarial attack algorithm and differential evolution algorithm, with the synthetic aperture radar (SAR) image feature sparsity considered. After accurately screening out the salient features that have a great impact on the model inference results, the DE-JSMA algorithm optimizes the appropriate feature values for the salient features. In order to verify its effectiveness more comprehensively, a new metric that combines the attack success rate with the average confidence interval of adversarial examples is proposed. The experimental results show that DE-JSMA extends JSMA, which can be used only for targeted attack scenario, to untargeted attack scenario without increasing too much time consumption but ensuring a high attack success rate, thus achieving sparse adversarial attack with higher reliability and better sparsity in both attack scenarios. The pixel perturbations of only 0.31% and 0.85% can achieve the untargeted and targeted attack success rates up to 100% and 78.79% respectively.
摘要
DNN易受攻击的特点使得以智能算法为识别手段的SAR-ATR系统也存在一定脆弱性。为验证其脆弱性, 结合SAR图像特征稀疏的特点, 在显著图对抗攻击算法和差分进化算法基础上提出了DE-JSMA稀疏攻击算法, 精确筛选出对模型推理结果影响较大的显著特征后, 为显著特征优化出合适的特征值。为了更全面地验证攻击的有效性, 构建了一种结合攻击成功率和对抗样本平均置信度的新指标Fc值。实验结果表明, 在没有增加过多耗时, 且保证高攻击成功率情况下, DE-JSMA将只能定向攻击的JSMA扩展到了非定向攻击场景, 且在2种攻击场景下均实现了可靠性更高、稀疏性更优的稀疏对抗攻击, 仅扰动0.31%与0.85%的像素即可达到100%与78.79%以上的非定向与定向攻击成功率。
Key words: synthetic aperture radar / automatic target recognition / deep learning / adversarial attack / sparse attack
关键字 : 合成孔径雷达 / 自动目标识别 / 深度学习 / 对抗攻击 / 稀疏攻击
© 2023 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
合成孔径雷达(synthetic aperture radar, SAR)广泛应用于地理勘测、军事信息处理等领域。由于SAR图像人工解译十分困难, 且SAR系统获取的数据量不断增加, 近年来SAR图像解译已转向智能化, 基于深度神经网络模型(deep neural network, DNN)的合成孔径雷达自动目标识别系统(synthetic aperture radar automatic target recognition, SAR-ATR)可自动提取特征, 大幅提高了识别准确率和效率[1-3]。但研究表明[4-9]DNN模型易受到对抗样本的攻击, 且对抗样本能够以高置信度被DNN模型误分类, 但人眼几乎无法辨别。
2014年, Szegedy等[10]首次发现DNN模型的脆弱性。而后, Goodfellow等[4]解释了这种“对抗攻击”现象存在的原因, 即DNN模型高维空间中的线性性质导致无限小的对抗扰动在DNN模型前向传播过程中不断积累, 最终引起输出的巨大变化。根据对抗扰动的疏密程度, 可将对抗攻击分为密集攻击和稀疏攻击。密集攻击通常以全尺寸分布的方式向输入图像添加扰动, 例如：Goodfellow等[4]提出了利用损失函数梯度的快速梯度符号方法(fast gradient sign method, FGSM); Moosavi-Dezfooli等[5]提出了基于超平面分类的攻击方法DeepFool; Carlini和Wagner[6]提出了C & W算法, 将距离度量引入到目标函数中, 迭代寻找其最优解。与密集攻击不同, 稀疏攻击主要需要考虑2个问题, 即扰动位置和扰动强度的选择, 例如：Papernot等[7]提出了基于雅各比矩阵的显著图攻击算法(Jacobian saliency map attack, JSMA), 构建显著图挑选显著特征, 并对其添加扰动; Su等[8]提出了OnePixel算法, 结合差分进化(differential evolution, DE)[11]算法确定扰动像素坐标和扰动强度, 利用DNN模型的结果引导进化方向; Modas等[9]提出了SparseFool算法, 是DeepFool算法在稀疏攻击上的应用, 但只能进行非定向攻击。
上述攻击算法均针对光学图像, 而近年来, 针对SAR-ATR系统的对抗攻击研究也开始涌现。2020年, Huang等[12]使用3种主流对抗攻击算法攻击基于DNN的SAR-ATR模型, 识别准确率降低90%以上, 首次证明了SAR-ATR模型的脆弱性。2021年, Du等[13]提出了Fast C & W算法, 引入编码器网络实现了原始样本到对抗样本的映射, 提高了算法实时性。最近, Peng等[14]提出了斑点变异攻击(speckle-variant attack, SVA)算法, 通过操纵斑点噪声模式增强对抗样本的迁移性。然而现有针对SAR图像的对抗攻击算法均为密集型, 扰动范围大, 物理可行性差。而且SAR图像由离散散射中心亮斑组成, 目标区域占比较小, 导致其特征冗余程度高[15], 因而采用稀疏攻击添加针对性扰动的方式可解释性更强, 稀疏对抗样本也更贴合物理世界中监测区域被部分遮挡或附着异物的情况。
为了解决上述问题, 针对SAR图像特征稀疏性, 本文在JSMA算法的基础上提出了一种新的稀疏攻击方法——基于差分进化的雅各比显著图攻击算法(differential evolution-Jacobian saliency map attack, DE-JSMA), 在精确筛选出对模型推理结果影响较大的显著特征的同时, 动态选择合适的特征值, 并延伸设计, 使其既可以定向攻击, 又可以非定向攻击。为了更全面地验证攻击有效性, 本文构建了一种结合攻击成功率和对抗样本平均置信度的新指标Fc值。实验结果表明, 在没有增加过多耗时, 且保证高攻击成功率的情况下, DE-JSMA实现了可靠性更高、稀疏性更优的稀疏攻击, 并且表现出了优越的重定向能力。
1 SAR-ATR系统攻击分析
SAR-ATR系统通常包括图像采集、数据预处理、深度神经网络训练和验证、深度识别模型测试和部署等几个重要的信息处理步骤, 这些步骤都具有潜在的安全问题。①图像采集阶段: 攻击者使用特定方式干扰SAR传感器的数据采集链路。在SAR成像的过程中, 攻击者可以设置不同的干扰模式来攻击SAR抗欺骗干扰技术。②图像预处理阶段: 在提取图像信息前, 需对原始图像数据进行一系列校正和预处理操作, 在这个过程中也会存在新的安全风险, 例如重采样攻击, 攻击图片被图像识别模型缩放到特定的空间分辨率后才会得以显现。③模型训练阶段: 典型的攻击方式包括投毒攻击和后门攻击。投毒攻击是指攻击者设法对训练数据进行某种恶意操作进而污染训练数据, 使原有数据的概率分布发生改变, 模型可用性被破坏的一种攻击方式。而后门攻击是指模型在训练阶段使用某些精心制作的恶意样本进行训练, 此模型对于正常样本的预测结果表现正常, 但对于某些具有特定属性的测试样本, 便可以触发后门使模型的预测结果受攻击者操控。④模型测试阶段: 典型的攻击方式是规避攻击, 规避攻击的一个代表性工作就是针对DNN模型的对抗攻击。⑤模型部署阶段: 典型的攻击方式包括面向设备的硬件攻击、操作系统攻击等。许多支持神经网络加速的开源软硬件平台的底层安全问题尚未得到充分验证, 这给模型部署带来了很大的安全风险。
本文的工作是针对SAR-ATR系统的模型测试阶段实施对抗攻击, 在图像分类任务中, 对抗攻击的目的是针对输入图像(即原始样本)X∈RH×W及其真实标签Y∈RJ, 找到一个人眼难以察觉的对抗扰动δ, 从而误导目标识别模型F: RH×W→RJ输出错误预测结果。衡量对抗扰动δ的大小通常使用Lp范数。对抗攻击的形式化表达如(1)式所示
式中：F为深度神经网络模型; X为原始样本; X′为对抗样本; Y为原始样本的标签; Y′为对抗样本的标签; δ为对抗扰动; D为样本取值范围, 图像中通常为像素值范围[0, 255];‖·‖p为度量对抗扰动大小的范数, p=0时, 范数值表示相较于原始样本, 对抗样本改变的像素个数大小; p=2时, 范数值表示对抗样本和原始样本之间的欧几里得距离。
由(1)式可知, 对抗攻击可看作一个在规定条件内最小化的优化问题, 但DNN模型高度非线性的性质导致此优化问题非线性且非凸, 因此找到这个问题的最优解并非易事。
2 DE-JSMA算法
本文将(1)式中的求解转化为最佳扰动位置与大小选择的问题, 因此, 设计的DE-JSMA算法主要分为3步。第一步是利用雅克比显著性计算的方法实现显著图的计算；第二步是利用算得的显著图确定要攻击的位置；第三步则是利用差分进化算法计算显著性图所在点的攻击强度, 最终得到对抗扰动δ, 将其添加到干净样本X上获得对抗样本X′从而实现有效的稀疏攻击, 整体框架图如图 1所示。在JSMA的基础上, 本文进行了延伸设计, 使得提出的DE-JSMA既可以实现非定向攻击, 也可以实现定向攻击, 具体的算法设计将在下文进行详细介绍。
 |
图1 DE-JSMA算法框架图 |
2.1 显著性检测方法
显著性检测方法主要分为以下2步:
1) 求前向梯度
前向梯度的定义是目标模型输入与隐藏层输出映射函数的雅各比矩阵, 可表示单个隐藏层输出关于单个输入特征的变化关系, 其公式为
式中：X为输入图像; F(·)为目标模型输入到隐藏层输出的映射函数; Fj为第j个隐藏层输出; xi为输入图像的第i个特征; M为输入图像的特征总数, 即像素总数; N为目标模型隐藏层的输出个数。
2) 计算显著图
JSMA算法提出了基于雅各比矩阵的显著图计算方法, 此方法只适用于定向攻击, 其公式为
式中, t为目标类别标签。
在定向攻击场景中选择显著特征时, 应当选取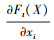 
为正且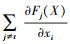 
为负的特征。
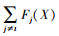为正, 则特征值xi增加时, Ft(X)会随之增加。同理, 
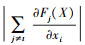为负, 则特征值xi增加时, 
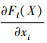会随之减小或者保持不变。而可选特征的显著值S(X, t)[i]定义为
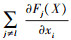与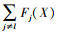 
的乘积, 可综合考虑所有前向梯度分量的影响, 特征显著值越高, 扰动该特征时更容易增大目标类别的输出结果或减小非目标类别的输出结果。
JSMA算法只实现了定向攻击, 本文将此算法推广到非定向攻击场景, 其公式为
式中，l为输入图像的真实标签。
在非定向攻击场景中选择显著特征时, 应当选取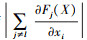 
为负且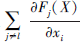 
为正的特征。
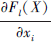为负, 则特征值xi增加时, Fl(X)会随之减小。同理, 
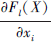为正, 则特征值xi增加时, 
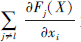会随之增大或者保持不变。而可选特征的显著值S(X, l)[i]定义为
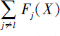与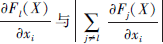 
的乘积, 特征显著值越高, 扰动该特征时更容易减小标签类别的输出结果或增大其他类别的输出结果。
2.2 差分进化算法
Storn和Price[11]提出差分进化算法, 采用基于群体的启发式搜索解决连续空间全局优化问题。DE算法通过有针对性地选择系统参数优化系统的某些属性, DE-JSMA中选取的待优化系统参数为挑选出的显著特征特征值。差分进化算法优化问题的标准流程是, 首先设计一个目标函数对问题目标进行建模, 该函数可结合任意约束。目标函数大多会将优化问题定义为最小化问题, 这种目标函数可被更准确地描述为成本函数。DE-JSMA中差分进化的目标函数fDE设为目标网络模型输出的目标类别置信度, 如(5)式所示, 以此来确定特征值进化的方向。
式中：c(X′(t))为对抗样本目标类别t的置信度；c(X′(l))为对抗样本标签类别l的置信度。
而后算法初始化种群即待优化系统参数的候选值, 循环执行变异、交叉和选择操作, 完成种群的进化, 直到算法迭代次数达到上限, 或种群最优解达到预设误差精度时, 算法结束。
算法1 DE-JSMA
输入 干净样本X; 标签类别l; 定向攻击的目标类别t;
神经网络模型输入到隐藏层输出的映射函数F;
攻击上限γ; 攻击步长n;
DE算法最大迭代次数Imax
输出 对抗样本X*
1) X*←X
2) while N≤γ and 攻击未成功 do
3) 利用(2)式计算前向梯度▽F(X*)
4) if非定向攻击then
5) 利用(4)式计算显著图
S=saliency_map(▽F(X*), l);
6) else if定向攻击then
7) 利用(3)式计算显著图
S=saliency_map(▽F(X*), t);
8) end if
9) 按照攻击步长n选取显著特征;
10) while j＜Imax do
11) 利用DE算法微调显著特征的特征值;
12) N←N+n;
13) end while
14) end while
DE-JSMA算法执行过程如算法1所示。开始攻击前, 需设置攻击方式(非定向攻击/定向攻击)、攻击步长n、DE算法最大迭代次数Imax和攻击上限γ。若攻击方式设为定向攻击, 则还要设置攻击的目标类别。攻击步长是指单次扰动的特征数量。攻击上限指扰动特征数量的上限, γ最大可设为16 384(即128×128)。由于显著图的计算需要较大计算成本, 因此为减少计算显著图的次数, 每轮需要选取多个显著特征, 即攻击步长n, 但n也不宜过大, 否则会造成后续差分进化算法寻优过程中计算成本增加。n默认为5。DE算法最大迭代次数Imax也不宜过大, 否则同样会造成耗时过长, 而且在单步攻击中迭代次数过多, 易使对抗扰动陷入局部最优解。Imax默认为3。
设置参数后, DE-JSMA将迭代攻击直至攻击成功或扰动特征数量超出攻击限制, 每轮攻击包含3个步骤: 首先计算前馈神经网络模型的“前向梯度”, 即模型输入到隐藏层输出映射函数的梯度(第3)步), 并利用前向梯度计算显著图(第4)~8)步); 然后基于显著图选取显著特征, 特征越显著表示对模型输出影响越大(第9)步); 最后利用差分进化算法寻优, 为选取的显著特征确定像素值(第10)~13)步)。每轮攻击结束判断是否攻击成功, 若成功则攻击结束, 否则进入下一轮攻击, 如此迭代直至攻击成功。
3 实验及分析
为了验证DE-JSMA的有效性, 本文在公开的SAR图像数据集MSTAR上分别对经典的DNN模型如AlexNet、VGG16以及ResNet18等进行攻击, 并以攻击成功率、Fc值以及平均扰动特征个数作为评价指标, 分别在定向攻击和非定向攻击场景下展开对比实验。
3.1 实验环境与实验设置
硬件环境为英特尔Silver 4210R处理器, 128 GB内存。软件环境为64位Ubuntu 20.04.1操作系统, 显卡为GeForce RTX 3090, 开发环境为Python 3.6.13, PyTorch 1.9.0。
实验采用包含10类目标的SAR图像数据集MSTAR, 攻击的3个目标模型在MSTAR训练集上的训练准确率分别为92.62%, 97.11%, 91.39%, 如表 1所示。本文从MSTAR测试集的每个分类分别随机选取10张图像, 选取的100张图像构成验证数据集, 用于测试对抗攻击算法, 3个模型攻击数据集上的分类准确率分别为91.00%, 97.00%, 91.00%, 如表 1所示。
3个目标模型的准确率 %
本文将与FGSM、C & W、DeepFool、SparseFool、JSMA、OnePixel 5个对抗攻击算法进行对比实验, 算法特性如表 2所示。
不同算法的特性表
3.2 评价指标
1) 攻击成功率
攻击成功率RAS是评价对抗攻击算法最常用的评价指标, 按定义可分为定向攻击和非定向攻击。定向攻击的攻击成功率表示在全部样本中, 可被模型分类为目标类别的比例, 其公式为
式中，I(·)为指示函数; Y(X′n)为对抗样本的预测类别; t(n)为第n个对抗样本的目标类别; N为可被正确分类的样本总数。
非定向攻击的攻击成功率表示在全部样本中, 可被模型错误分类的对抗样本的比例, 其公式为
式中，y(n)为第n个干净样本的标签类别。
2) Fc值
对抗样本的可靠性可通过其对抗类别的置信度来衡量, 置信度越高, 表示对抗样本具备越多对抗类别的特征, 进而表明对抗样本攻击性能就越强。当目标模型发生微调时, 置信度高的对抗样本仍能保持攻击效果的概率更高。RAS是评价对抗攻击算法最重要的指标, 可靠性相对次要, 因此本文将攻击成功率和与对抗样本置信度相关的参数C结合起来, 将二者的调和平均数定义为一个新指标Fc, 有助于综合评价对抗样本的质量并提供更准确的判断依据, Fc值越大, 表示对抗样本在保证攻击有效性的前提下更可靠, 其公式为
式中: c(X′i(t))为第i个对抗样本目标类别t的置信度; S为对抗样本总数; l为对抗样本的标签类别。
3) 平均扰动特征个数Navg
DE-JSMA算法对扰动进行L0范数约束的稀疏对抗攻击。L0范数可表示相较于原始样本, 对抗样本改变的像素个数, 因此本文将L0范数的平均值Navg作为衡量对抗扰动稀疏性和对抗样本隐蔽性的指标, 其公式为
式中：S为对抗样本总数；I(·)为指示函数。
4) 平均耗时Tavg
平均耗时是评价攻击算法的一项重要评价指标, 用于衡量攻击算法的实时性, 其公式为
式中，Ti为第i个对抗样本的攻击耗时, 单位为s。
3.3 实验结果与分析
本节实验中, 攻击上限γ设为16 384, 即可攻击任意多个特征, 攻击步长n和最大迭代次数Imax分别采用默认值5和3。攻击的可视化结果如图 2所示。
 |
图2 DE-JSMA对抗攻击可视化展示 |
非定向攻击实验对比结果如表 3所示。DE-JSMA攻击成功率均达到100%, 攻击效果非常优越。然而Fc值结果并不突出, 因为DE-JSMA非定向攻击时, 扰动优化的目标是样本偏离原有决策边界, 而非让某一对抗类别置信度增加, 这就导致非定向攻击中对抗样本置信度往往较低, 进而导致Fc值较低, 但并不影响DE-JSMA的有效性。从Navg来看, DE-JSMA仅扰动0.09%~0.31%的像素就达到了100%的攻击成功率, 且扰动特征数量比第二稀疏的OnePixel少71.67%~91.62%, 攻击稀疏性最好, 这正是DE-JSMA的优势所在, 将扰动集中到极少数的像素上, 大大增加了攻击的物理可实现性。
非定向攻击对比结果
针对定向攻击, 本文同样在MSTAR数据集上展开, 并对其10个类别全部进行了定向攻击。为了综合对比攻击效果, 实验结果为各项指标全类别结果的均值, 如表 4所示。从攻击成功率RAS来分析, DE-JSMA和JSMA有着相似的表现性能, 均远超其他算法, 但在Fc值这一评价指标下, DE-JSMA有着鲜明的优势, 生成的对抗样本在保证有效性的同时表现出最优的可靠性。与非定向攻击不同, DE-JSMA在挑选出显著像素后, 差分进化算法能有效利用目标类别对目标模型进行有针对性的优化, 进而优化得到具有高置信度的对抗样本, 即可靠的对抗样本。由此可得, DE-JSMA更适用于定向攻击。除此之外, DE-JSMA同样表现出最佳的稀疏性, 在扰动0.60%~0.85%的极少数像素的情况下实现定向攻击, 大大提升了攻击的实用价值。
定向攻击对比结果
针对SAR-ATR系统高实时性的特点, 所提出的攻击算法要有一定的时效性, 因此将平均耗时Tavg设置成另一重要指标。DE-JSMA自身具有稀疏特性, 因此只和同类型的稀疏算法进行对比。稀疏攻击算法在非定向攻击和定向攻击时的平均耗时对比结果如表 5所示, 其中定向攻击的平均耗时为全类别平均耗时的均值。
稀疏攻击平均耗时对比结果 s
由表 5可知，非定向攻击时, DE-JSMA耗时最短, 均远远低于OnePixel, 与之相差1~2个数量级。然而在定向攻击时, 尽管计算一次显著图选取多个显著特征, 这种做法可起到省时的作用, 但差分进化算法收敛缓慢, 优化确定显著特征的像素值的过程会耗费大量时间, 因此DE-JSMA比JSMA耗时略高, 但若将差分进化算法替换成更先进的优化算法, 算法的时间性能将会有进一步的提升。
为了更全面地展示DE-JSMA算法定向攻击的性能, 图 3以热力图的方式展示了针对3种目标模型全类别的定向攻击结果。热力图纵轴的0~10表示干净样本的源类别, 每个源类别从测试数据集中选取10个干净样本, 共选取出100个干样本，横轴的0~10表示对抗样本的目标类别, 图中数字表示源类别10个干净样本中，成功攻击成目标类别的对抗样本个数, 热力图数值越大, 颜色越深, 表示该数值对应的源类别被攻击成目标类别的样本数越多, 即该源类别更易被攻击成目标类别。单张热力图中定向攻击成功总次数除以定向攻击发起总次数可以计算得到, DE-JSMA算法定向攻击AlexNet、VGG16和ResNet18时, 分别能以79.67%, 93.56%, 91.00%的成功率将干净样本重定向为任意目标类别, 这进一步说明了DE-JSMA在定向攻击中的有效性。
 |
图3 定向攻击源类别与目标类别相关性热力图 |
4 结论
基于DNN的SAR-ATR系统存在严重的安全问题。考虑到SAR图像的特征稀疏性, 本文提出了DE-JSMA稀疏攻击算法, 在精确筛选出对模型推理结果影响较大的显著特征的同时, 动态选择合适的特征值。本文还构建了一种结合攻击成功率和对抗样本平均置信度的新指标Fc值, 来全面评价攻击算法的有效性和可靠性。实验结果表明, 在没有增加过多耗时, 且保证高攻击成功率的情况下, DE-JSMA在定向、非定向2种攻击场景中均实现了可靠性更高、稀疏性更优的稀疏攻击, 并且表现出了优越的重定向能力。后续工作中需进一步提升算法执行效率, 以满足SAR-ATR系统的高实时性。
References
- CHEN S, WANG H, XU F, et al. Target classification using the deep convolutional networks for SAR images[J]. IEEE Trans on Geoscience and Remote Sensing, 2016, 54(8): 4806–4817. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- SHARIFZADEH F, AKBARIZADEH G, SEIFI K Y. Ship classification in SAR images using a new hybrid CNN-MLP classifier[J]. Journal of the Indian Society of Remote Sensing, 2019, 47(4): 551–562. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- VINT D, ANDERSON M, YANG Y, et al. Automatic target recognition for low resolution foliage penetrating SAR images using CNNs and GANs[J]. Remote Sensing, 2021, 13(4): 596. [Article] [CrossRef] [Google Scholar]
- GOODFELLOW I J, SHLENS J, SZEGEDY C. Explaining and harnessing adversarial examples[C]//International Conference on Learning Representations, 2015 [Google Scholar]
- MOOSAVI-DEZFOOLI S M, FAWZI A, FROSSARD P. DeepFool: a simple and accurate method to fool deep neural networks[C]//Computer Vision and Pattern Recognition, 2016: 2574–2582 [Google Scholar]
- CARLINI N, WAGNER D. Towards evaluating the robustness of neural networks[C]//2017 IEEE Symposium on Security and Privacy, 2017: 39–57 [Google Scholar]
- PAPERNOT N, MCDANIEL P, JHA S, et al. The limitations of deep learning in adversarial settings[C]//European Symposium on Security and Privacy, 2016: 372–387 [Google Scholar]
- SU J, VARGAS D V, SAKURAI K. One pixel attack for fooling deep neural networks[J]. IEEE Trans on Evolutionary Computation, 2019, 23(5): 828–841. [Article] [CrossRef] [Google Scholar]
- MODAS A, MOOSAVI-DEZFOOLI S M, FROSSARD P. SparseFool: a few pixels make a big difference[C]//2019 IEEE Conference on Computer Vision and Pattern Recognition, 2019: 9079–9088 [Google Scholar]
- SZEGEDY C, ZAREMBA W, SUTSKEVER I, et al. Intriguing properties of neural networks[C]//International Conference on Learning Representations, 2014 [Google Scholar]
- STORN R, PRICE K. Differential Evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341–359. [Article] [CrossRef] [Google Scholar]
- HUANG T, ZHANG Q, LIU J, et al. Adversarial attacks on deep-learning-based SAR image target recognition[J]. Journal of Network and Computer Applications, 2020, 162: 102632. [Article] [CrossRef] [Google Scholar]
- DU C, HUO C, ZHANG L, et al. Fast C & W: a fast adversarial attack algorithm to fool SAR target recognition with deep convolutional neural networks[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4010005 [Google Scholar]
- PENG B, PENG B, ZHOU J, et al. Speckle-variant attack: toward transferable adversarial attack to SAR target recognition[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 4509805 [Google Scholar]
- ZHOU Juanfan, SUN Hao, LEI Lin, et al. Sparse adversarial attack of SAR image[J]. Journal of Signal Processing, 2021, 37(9): 1633–1643 (in Chinese) [Google Scholar]
All Tables
All Figures
|
图1 DE-JSMA算法框架图 |
| In the text | |
|
图2 DE-JSMA对抗攻击可视化展示 |
| In the text | |
|
图3 定向攻击源类别与目标类别相关性热力图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.