| Issue |
JNWPU
Volume 41, Number 2, April 2023
|
|
|---|---|---|
| Page(s) | 253 - 263 | |
| DOI | https://doi.org/10.1051/jnwpu/20234120253 | |
| Published online | 07 June 2023 | |
Reliability analysis of flap deflection angle based on collaborative intelligent moving Kriging model
基于协同智能移动Kriging的襟翼偏角可靠性分析
1
The First Aircraft Research Institute of AVIC, Xi'an 710089, China
2
School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China
3
Institute of Reliability and Operation Support Engineering, Northwestern Polytechnical University, Xi'an 710072, China
Received:
15
June
2022
To effectively monitor the reliability of civil aircraft flap deflection angle, combined with the quick access recorder(QAR), the collaborative intelligent moving Kriging(CIMK) method is proposed by absorbing the Kriging model, decomposition and co-ordination strategy, equilibrium optimizer(EO), and moving least square(MLS). Among them, the decomposition coordination strategy is used to deal with the relationship between the flaps left and right deflection angles. MLS is employed to select effective modeling samples and solve the undetermined coefficients of Kriging model. EO method is applied to determine optimizing the local compact support region radius of MLS. Firstly, the fault reason for flap left-right asymmetry is analyzed to clarify the main characteristic parameters in QAR data. Secondly, combined with the QAR data of relevant influencing parameters, the civil aircraft flap deflection model(limit state function) is constructed by using CIMK. Then, the reliability and influence of civil aircraft flap deflection angle are analyzed by Monte Carlo(MC) sampling method. The results show that when the flap deflection angle is 3°, the reliability is 0.450 2, and the important factors affecting the flap deflection angle are Mach number, left angle of attack, right angle of attack, etc. Compared with the response surface method(RSM), Kriging, support vector machine(SVM), and back-propagation-artificial neural network(BP-ANN), the average absolute error accuracy of the proposed method is relative improved by 53.02%, 51.43%, 49.03%, and 44.04%, the average relative error accuracy is relative improved by 68.36%, 66.76%, 64.41%, and 62.64%, and the modeling efficiency is relative improved by 50.62%, 26.35%, and 43.01% respectively compared with Kriging, SVM and BP-ANN. When the number of simulations is 103, the analysis accuracy is relative improved by 8.82%, 7.25%, 6.22%, and 3.98% respectively.
摘要
为了有效开展民机襟翼偏角可靠性监测, 结合快速存取记录器(quick access recorder, QAR)数据, 基于Kriging模型, 引入分解协调策略、平衡器优化(equilibrium optimizer, EO)算法和移动最小二乘(moving least square, MLS), 提出了一种基于协同智能移动Kriging(collaborative intelligent moving Kriging, CIMK)方法。其中, 分解协调策略用于处理襟翼左右偏角之间的关系, MLS用于选取有效建模样本并实现Kriging模型待定系数求解, EO算法用于确定MLS最优的紧支撑域半径。针对襟翼左右不对称进行故障原因分析, 明确QAR数据中影响襟翼偏角的主要特征参数; 结合相关影响参数的QAR数据, 运用CIMK实现民机襟翼偏角模型(极限状态函数)的构建; 基于构建的CIMK模型, 通过Monte Carlo抽样方法进行民机襟翼偏角可靠性及影响性分析; 以某型国产民机襟翼偏角为例, 对所提出的方法进行可行性分析。研究结果表明: 当襟翼偏角为告警许用值3°时, 可靠度为0.450 2, 影响襟翼偏角的因素重要程度依次为马赫数、左攻角、右攻角等。与RSM、Kriging、SVM和BP-ANN方法对比发现: 在建模特性方面, 所提方法平均绝对误差精度相对提高了53.02%, 51.43%, 49.03%和44.04%, 平均相对误差精度相对提高了68.36%, 66.76%, 64.41%和62.64%;建模效率相对于Kriging、SVM和BP-ANN分别提高了50.62%, 26.35%和43.01%;在仿真性能方面, 当仿真次数为103次时, 分析精度分别提高了8.82%, 7.25%, 6.22%和3.98%。
Key words: civil aircraft / flap deflection angle / reliability analysis / collaborative intelligent moving Kriging / QAR
关键字 : 民机 / 襟翼偏角 / 可靠性分析 / 基于协同智能移动Kriging方法 / QAR
© 2023 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
襟翼系统在民机起飞及着陆过程中具有保持升力和减速的重要作用,其可靠性对民机的安全运行至关重要[1-2]。近年来,民机襟翼系统功能失效事件常有发生,如EMB145、运7/8、B737/747/767、BAE146、B767等都曾出现过襟翼系统故障的问题[3-4]。襟翼左右不对称作为民机襟翼系统最常见的故障之一[5-8],可能会导致民机飞行过程中失去平衡,造成安全事故。因此,为了避免襟翼左右不对称故障的发生,需要对民机襟翼偏角进行可靠性分析。
近年来,围绕民机系统可靠性分析问题,国内外学者开展了许多研究。马超等[9]基于蒙特卡洛(Monte Carlo, MC)模拟方法,利用快速存取记录器(quick access recorder, QAR)数据进行了襟翼左右偏角监测分析;赵洪利等[10]基于MC法,对航空发动机发生故障的可能性进行了风险评估;朱晓炜等[11]结合QAR数据,通过统计分析法开展了襟翼偏角研究。上述基于MC和统计分析方法虽然具有较高的精度,但需要大量数据作为支撑,且效率较低。为了避免MC和统计分析方法的弊端,许多学者探究了基于代理模型的民机系统可靠性分析。贾宝惠等[12]采用响应面(response surface method, RSM)方法对起落架结构进行了安全性分析;Keshtegar等[13]通过改进的RSM方法,开展了航空涡轮叶盘可靠性分析;马小骏等[14]基于最小二乘支持向量机提出了一种航空发动机性能可靠性监测方法;Chen等[15]提出了一种基于相似度选择遗传算法的支持向量机模型,对起落架的可靠性进行了分析;Zhou等[16]提出改进的神经网络方法,开展了民机APU监测分析。冯蕴雯等[17-18]将神经网络与随机森林结合,提出了一种飞机动力装置可靠性分析方法;Lu等[19]提出了改进的Kriging模型,对发动机涡轮叶盘运行状态进行了可靠性分析;Teng等[20]基于Kriging模型提出了一种发动机叶尖径向间隙可靠性分析方法。上述代理模型方法在一定程度上减少了民机系统监测所需数据量,但建模过程中,并没有充分利用已知样本信息,导致其分析精度不能满足工程需求。另外,对于涉及多表征参数的高非线性民机系统可靠性分析问题,其分析精度不能满足工程需求。而移动最小二乘的提出为合理利用已知样本信息提供了新的思路[21],同时分解协调策略在复杂数学函数求解中的应用也为解决高非线性问题提供了借鉴[22]。
为实现民机襟翼偏角的可靠性监测,本文基于QAR数据,将Kriging模型、分解协调策略、平衡器优化(equilibrium optimizer, EO)算法和移动最小二乘(moving least square, MLS)方法有效融合,提出一种基于协同智能移动Kriging(collaborative intelligent moving Kriging, CIMK)方法,用于实现民机襟翼偏角的可靠性分析。首先,分析民机襟翼左右不对称故障原因,确定QAR数据中影响襟翼偏角的主要特征参数;然后,结合特征参数的QAR数据,基于CIMK方法建立襟翼偏角极限状态函数并开展可靠性与影响性分析;最后以某型国产民用飞机襟翼偏角为案例验证所提方法的有效性与可行性。
1 襟翼左右不对称故障机理分析
1.1 襟翼左右不对称故障原因分析
襟翼左右不对称故障是由于襟翼左偏角与襟翼右偏角之间的差值大于一定角度而引发的故障,根据机组操作手册(flight crew operating manual, FCOM)中的要求,当发生襟翼左右不对称故障时,机组不可使用襟翼备用收放系统继续将襟翼放下。在民机起飞和着陆过程中,襟翼左右不对称故障发生的原因主要包括:
1) 液压系统损坏或泄露:液压管路负责供压给机械装置,一旦液压管路及其连接件失效,将引发损伤和漏油,导致襟翼偏转失去动力源;
2) 控制组件传达指令错误或失灵:控制组件负责传递作动指令,并且根据传感器发送的信号判断襟翼的运动状态,控制组件的失效会引发襟翼的非指令作动或错误传达襟翼运动状态等;
3) 机械装置强度或运动精度失效:机械装置是实际作动的执行者,由于机械部件的设计、质量及维护等原因,随着机体持续运行,襟翼部件的抗腐蚀和润滑油的保持能力降低,造成诸如襟翼扭力管、齿轮箱、支架轴承等部件过度磨损,阻力增大,左右襟翼的磨损和润滑状况不一致,使得左右襟翼动作速度不一致,进而发生襟翼不对称故障。
1.2 襟翼左右不对称故障表征参数提取
针对襟翼左右不对称故障,结合QAR监测参数类型,提取影响襟翼偏角的表征参数,其遵循原则如下:
1) 在民机运行过程中襟翼偏转可能会导致民机发生偏航或滚转,但与俯仰无关。因此,进行表征参数选择时,结合监测活动翼面的76种QAR参数类型,选取与民机偏航和滚转有关的参数,排除仅与民机俯仰有关的参数。
2) 民机在飞行时,造成襟翼偏角有很多不确定因素,除上述因素外,还需考虑其他因素的影响,主要依据飞机升力公式
式中:CL为升力系数, 通常是通过风动试验获取, 与攻角有关; ρ为飞行高度处的空气密度; v为民机的空速; Sw为机翼的平面投影面积。ρ与飞行高度有关, v与马赫数、风速、风向有关。根据上述分析, 需考虑QAR中的参数为: 飞行高度、马赫数、风速、风向、左右攻角。本文选取民机起飞阶段作为襟翼偏角研究对象, 某型国产民机起飞阶段襟翼偏角差绝对值如图1所示。
由图1可知, 起飞阶段襟翼工作状态可以划分为襟翼完全放开、襟翼收回、襟翼完全收回状态, 襟翼左右不对称故障主要发生在襟翼收回过程中, 本文主要针对起飞阶段襟翼收回过程的偏角进行分析。对襟翼收回过程获取的表征参数进行如下处理:
1) 参数监测重复: 对于同一参数多传感器监测问题, 左右两侧选择同一位置传感器监测参数;
2) 参数监测为布尔值: 对于表征参数监测参数为布尔值问题, 不考虑作为襟翼偏角的影响因素;
3) 参数监测为定值: 对于选取起飞阶段的表征参数监测参数为定值问题, 不考虑作为襟翼偏角的影响因素。
 |
图1 起飞阶段襟翼的工作状态 |
2 CIMK方法原理
2.1 基于CIMK的襟翼偏角可靠性分析流程
为实现襟翼偏角的可靠性分析, 本文将分解协调策略、ML、EO算法和Kriging模型相结合, 提出了CIMK方法。其中, 结合分解协调策略处理襟翼左右偏角之间的关系, 依据ML获取有效建模样本, 运用Kriging模型建立襟翼偏角与表征参数之间的关系模型, 进而通过EO确定最优紧支撑域半径。基于CIMK的襟翼偏角可靠性分析流程如图2所示。
由图2可知, 基于CIMK的襟翼偏角可靠性分析主要包括有效样本获取、模型建立、可靠性分析、影响性分析, 具体流程如下:
1) 有效样本获取:通过QAR数据采集, 获取初始样本信息, 进而划分为训练样本与测试样本, 初始化紧支撑域半径并从训练样本中选取有效训练样本;
2) 模型建立:基于有效训练样本建立初始基于CIMK的襟翼偏角模型, 通过优化目标函数验证所建立模型是否满足精度要求, 如果不满足, 则需通过EO算法再次计算紧支撑域半径, 重新选择有效训练样本, 直到满足精度要求为止;
3) 可靠性分析:首先确定襟翼偏角极限状态函数, 然后结合MC技术分析襟翼左右偏角可靠性;
4) 影响性分析:基于襟翼偏角可靠性分析结果开展影响性分析, 确定输入变量的影响性及影响概率。
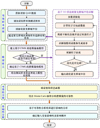 |
图2 基于CIMK的襟翼偏角可靠性分析流程 |
2.2 CIMK数学模型
通过目标层、子模型层(第一子模型层、第二子模型层)、变量层复合函数说明CIMK方法原理。基于分解协调策略, 将复合函数依次分解至变量层, 其原理示意图如图3所示。
如图3所示, f(·)为目标层输出响应与第一子模型层输出响应之间的关系, f(s)(·)为第s个第一子模型层输出响应与第二子模型层输出响应之间关系, f(sd)(·)为第s个第一子模型层的第d个第二子模型层输出响应与变量层之间关系。
目标层输出响应可以表示为
式中:s是第一子模型层中的输出响应数量; y(i)(i=1, 2, …, s)是第i个第一子模型层的分解模型, 即
式中:d是第二子模型层中的输出响应数量; y(ij) (j=1, 2, …, d)表示第i个第一子模型层中第j个第二子模型层的分解子模型, 即
式中,x(ij)是第i个第一子模型层包含的第j个第二子模型层的相关变量。
为建立第i个第一子模型层中第j个第二子模型层的分解子模型y(ij), 引入具有局部紧支撑域的移动最小二乘, 将圆作为紧支撑区域[23], 从训练样本中选择有效样本, 为了说明紧支撑区域获取有效样本的基本原理, 以二维样本空间(u, v)为例进行说明, 如图4所示。
由图4可知, 在m个训练样本中, 每个样本作为中心点O(用红色点表示), 计算其他样本点(用蓝色点表示)距离中心点O的距离为r1(ij), r2(ij), …, rm-1(ij), 距离最大值为rmax(ij)=max{r1(ij), r2(ij), …, rm-1(ij)}, 最小值为rmin(ij)=min{r1(ij), r2(ij), …, rm-1(ij)}。以初始紧支撑域半径为r0(ij)(rmin(ij)<r0(ij)<rmax(ij))选取有效样本点, 获得m′个有效样本为{(x1(ij), y1(ij)), (x2(ij), y2(ij)), …, (xm′(ij), ym′(ij))}, 然后建立Kriging模型, 其输出响应y(ij)与输入变量的函数关系可以表示为
式中:x(ij)=(x1(ij), x2(ij), …, xn(ij))T表示输入变量;n为输入变量的维数; f(ij)(x(ij))=[f1(ij)(x(ij)), f2(ij)(x(ij)), …, fk(ij)(x(ij))]T表示Kriging模型的基函数, k为基函数的个数; β(ij)=[β1(ij), β2(ij), …, βk(ij)]表示基函数f(ij)(x(ij))回归系数; Z(ij)(x(ij))表示均值为0、标准差为δ2的高斯过程。本文采用二次多项式作为基函数的形式, 因为它具有较好的拟合精度[24-25], 公式(5)可以写为
式中:a(ij)是常数系数;bi′(ij)是第i′个输入变量的线性系数; ci′j′(ij)是第i′行j′列的二项式系数, i′, j′=1, 2, …, n。基函数回归系数β(ij)为
Z(x(ij))具有如下特性
式中:xp(ij)和xq(ij)(p, q=1, 2, …, m′)为第p个和第q个输入变量样本; θ(ij)为Kriging模型的超参数; 输入变量xp(ij)和xq(ij)的相关系数R(·)为
式中:θi′(ij)为Kriging模型第i′个超参数; xp, i′(ij)和xq, i′(ij)为第i′个分量中第p个和第q个输入样本。
为了获取θ(ij), β(ij)和σ2的值, 运用梯度下降法对极大似然函数进行求解, 即
式中: 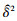 为预测方差; G(ij)=R(ij)W(ij)是加权相关系数矩阵。
为预测方差; G(ij)=R(ij)W(ij)是加权相关系数矩阵。
相关函数矩阵R(ij)为
预测方差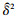 为
为
式中:Y(ij)=(y1(ij), y2(ij), …, ym′(ij))T表示m′个输入变量对应的输出变量; F(ij)=[f(x1(ij)), f(x2(ij)), …, f(xm′(ij))]T; 加权矩阵W(ij)由三次样条函数确定[26]
式中: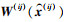 为计算点
为计算点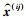 处的加权矩阵; r0(ij)为初始紧支撑域半径;
处的加权矩阵; r0(ij)为初始紧支撑域半径; 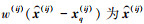 与第q个有效样本点xq(ij)的权值;
与第q个有效样本点xq(ij)的权值; 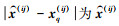 与第q个有效样本点xq(ij)的距离。
与第q个有效样本点xq(ij)的距离。
以平均相对误差作为优化目标函数为
式中:ypre(ij)(xq(ij))为第q个有效样本点的输出响应预测值; ytrue(ij)(xq(ij))为第q个有效样本点的输出响应真实值。
根据优化目标函数值, 判断所建立模型是否满足精度需求, 若不满足, 则采用EO算法实现紧支撑域半径r(ij)的寻优, 其适应度函数为优化目标函数。其中, EO算法具有求解精度高、全局探索能力强等优势[27], 粒子浓度更新方式为
式中:F为指数项系数;G为质量生成速率;Xeq为平衡池中的候选粒子;V是常数单位, λ为[0, 1]之间的随机数。
EO算法对紧支撑域半径r(ij)寻优过程如图5所示。
由图5可知, 紧支撑域半径r(ij)在[rmin, rmax]区间变化, 直至EO算法迭代完成时, 获得最优紧支撑域半径ropt(ij)。进而选取最优有效训练样本, 最终确定输出响应y(ij)与输入变量的函数关系模型。
同理,第二子模型层第i个分解子模型和目标层输出响应为
式中:i″, j″=1, 2, …, n′, n′为第二子模型层变量个数;i''', j'''=1, 2, …, n″, n″为第一子模型层变量个数;a(i), bi″(i), ci″j″(i)分别为第二子模型层分解子模型的常数项系数、一次项系数、二次项系数;a, bi''', ci'''j'''分别为第一子模型层分解子模型的常数项系数、一次项系数、二次项系数; Z(i)(x(i))为第二子模型层分解子模型高斯随机过程;Z(x)为第一子模型层分解子模型高斯随机过程。
通过上述分析, 结合分解策略将总目标分解为多个子模型, 针对每个子模型, 运用ML选取有效训练样本点, 建立Kriging子模型, 通过EO算法选取子模型最优紧支撑域半径, 进而结合协调策略协调各子模型与总目标之间的关系, 最终确定研究对象的功能函数。
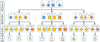 |
图3 分解协调策略原理示意图 |
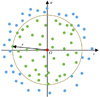 |
图4 紧支撑区域获取有效样本的原理 |
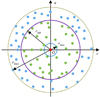 |
图5 EO算法寻找最优紧支撑域半径过程示意图 |
2.3 CIMK可靠性分析
结合CIMK数学模型, 构建民机襟翼偏角极限状态函数为
式中, yallow为襟翼偏角许用值。
襟翼偏角系统安全和失效状态通过失效域指示函数Ih(x)表示
式中:Ih(x)=0表示安全状态;Ih(x)=1表示失效状态。
通过MC法对(18)式进行大量仿真抽样, 襟翼偏角失效概率和可靠度可以表示为
式中:N为样本数量;Nf为失效样本数量。
2.4 CIMK影响性分析
为了研究不同输入变量的变化对襟翼偏角可靠度的影响, 结合可靠性分析结果进一步开展影响性分析。影响性为襟翼偏角可靠度对某一随机输入变量均值的偏导, 当Ih(x) < 0时
式中, μx为输入变量的均值。在均值点处的影响性Sj为
通过影响概率描述输入变量对输出响应的影响程度Ij, 即
式中, I1+I2+…+IN=1。
3 案例分析
3.1 襟翼偏角样本获取及模型构建
以某型国产民用飞机襟翼系统为研究对象, 对60个航班进行QAR数据采集, 然后通过数据处理、筛选等得到样本数量800组, 其中, 500组作为训练样本, 300组作为测试样本。假定影响襟翼偏角的表征参数(输入变量)相互独立, 近似服从正态分布, 分布特征如表1所示。
基于500组训练样本,建立了襟翼左偏角模型yleft(1)和襟翼右偏角模型yright(2)。由于襟翼左偏角与襟翼右偏角呈非负差值关系,结合协调策略,襟翼偏角模型Ytotal可以表示为
襟翼偏角输入变量分布特征
3.2 襟翼偏角可靠性分析
根据飞机维修手册(aircraft maintenance manual, AMM)规定, 当襟翼左右角度差值超过9°时, 发生襟翼左右不对称故障。但实际操作时, 角度差大于3°就会进行故障报告, 为避免不安全事件的发生, 目前一些航空公司监控的阈值为3°, 超过3°系统会有告警提示, 因此选择3°作为许用值yallow, 则极限状态函数为
通过对襟翼偏角极限状态函数执行不同次数的MC抽样模拟, 实现可靠度收敛性分析, 如图6所示。
由图6可知, 当许用值为3°时, 襟翼偏角的可靠度随样本数的增加收敛于0.450 2, 告警概率为0.549 8。
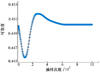 |
图6 可靠度收敛分析 |
3.3 襟翼偏角可靠性分析
当许用值为3°时, 襟翼偏角影响性分析结果如图7和图8所示。
基于图7~8中的襟翼偏角输入变量影响性及影响概率分析可以看出,襟翼偏角参数影响性分析结果为:左攻角、左副翼偏角、襟/缝翼控制手柄、航迹角、马赫数、标准高度、风向与襟翼偏角呈正相关关系;偏航角、滚转角、方向舵位置、控制杆位置、控制轮位置、风速、右攻角、右副翼偏角与襟翼偏角呈负相关关系。依据分析结果,影响襟翼偏角的因素重要性排序依次为马赫数、左攻角、右攻角、右副翼偏角、方向舵位置、襟/缝翼控制手柄、航迹角、左副翼偏角、滚转角、控制轮位置、偏航角、控制杆位置、风速、风向、标准高度。
 |
图7 襟翼偏角影响性分析柱状图 |
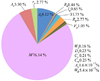 |
图8 影响概率分析 |
4 CIMK方法验证
4.1 建模特性验证
为说明CIMK方法在建模特性方面的可行性, 结合500组训练样本, 分别通过RSM、Kriging、支持向量机(support vector machine, SVM)、BP神经网络(back-propagation-artificial neural network, BP-ANN)建立襟翼偏角功能函数模型, 将绝对误差Eab、平均绝对误差Eaa、相对误差Ere和平均相对误差Ear作为评价准则[28-29], 其中Eab, Eaa, Ere和Ear第j个计算原理为
式中:ŷj表示襟翼偏角功能函数模型第j(j=1, 2, …, m)个预测值;ytrue, j第j个襟翼偏角真实值;Eab, j为第j个预测值与真实值的绝对误差;Ere为第j个预测值与真实值的相对误差;Ere为m个预测值与真实值的平均相对误差。
结合200组测试样本, 通过Eab, Eaa, Ere和Ear评价RSM、Kriging、SVM、BP-ANN和CIMK拟合精度, 其分析结果分别如图9~10、表2所示。
由表2可知,CIMK的平均绝对误差(0.474°)远低于RSM、Kriging、SVM和BP-ANN的平均绝对误差,相对提高精度分别为53.02%, 51.43%, 49.03%和44.04%;CIMK的平均相对误差(0.684°)远低于RSM、Kriging、SVM和BP-ANN的平均绝对误差,相对提高精度分别为68.36%, 66.76%, 64.41%和62.64%;CIMK的建模时间(4.36 s)低于Kriging、SVM和BP-ANN的建模时间,建模效率分别相对提高50.62%, 26.35%和43.01%。由图9~10可知,结合200组训练样本,CIMK绝对误差、相对误差波动较小且接近0,具有较好的鲁棒性。通过上述分析可知,相比于RSM、Kriging、SVM和BP-ANN,CIMK具有更好拟合精度与建模效率。
 |
图9 基于测试样本的RSM、Kriging、SVM、BP-ANN与CIMK的绝对误差对比 |
 |
图10 基于测试样本的RSM、Kriging、SVM、BP-ANN与CIMK的相对误差对比 |
拟合精度与建模效率分析
4.2 仿真性能验证
为了验证CIMK在仿真性能方面的有效性,在相同的计算环境下,以真实值作为参考,采用RSM、Kriging、SVM、BP-ANN和CIMK分别对襟翼偏角模型进行102、103和104仿真模拟,其仿真性能分析结果如表3~4所示。
由表3~4可知,在不同仿真次数下,CIMK的分析结果与真实值较为接近,其分析精度高于RSM、Kriging、SVM和BP-ANN。当仿真次数为103次时,与RSM、Kriging、SVM和BP-ANN相比,CIMK的分析精度分别相对提高了8.82%, 7.25%, 6.22%和3.98%。因此,CIMK在襟翼偏角可靠性分析的仿真性能方面具有一定的优势。
5种方法的可靠度
5种方法的分析精度 %
5 结论
基于Kriging模型,结合分解协调策略、EO算法与ML,提出了CIMK方法,结合QAR数据,实现了民机襟翼偏角可靠性分析,并通过对比验证了所提方法的有效性,主要结论如下:
1) 分析了民机襟翼左右不对称故障原因,提取了影响襟翼偏角的攻角、偏航角、马赫数等共表征参数;
2) 提出CIMK方法,基于某型国产民机QAR数据,实现了襟翼偏角可靠性分析及影响性分析,通过仿真模拟,当襟翼偏角为告警许用值3°时,可靠度为0.450 2;影响性襟翼偏角的表征参数从主到次依次为马赫数、左攻角、右攻角、右副翼偏角、方向舵位置、襟/缝翼控制手柄、航迹角、左副翼偏角、滚转角、控制轮位置、偏航角、控制杆位置、风速、风向、标准高度。
3) 在建模特性方面,与RSM、Kriging、SVM和BP-ANN方法相比,所提CIMK具有更好拟合精度与建模效率。
4) 在仿真性能方面,所提CIMK方法分析精度高于RSM、Kriging、SVM和BP-ANN方法,当仿真次数为103次时,分别相对提高了8.82%, 7.25%, 6.22%和3.98%。
5) 所提出的方法可为国产民机襟翼系统的日常运行、故障诊断、故障预测等提供参考。
References
- ZHOUC, CHANGQ, ZHAOH, et al. Fault tree analysis with interval uncertainty: a case study of the aircraft flap mechanism[J]. IEEE Trans on Reliability, 2020, 99: 1–13 [Google Scholar]
- ZHOUChangcong, CHANGQi, ZHOUChunping, et al. Fault tree analysis of an aircraft flap systembased on a non-probability model[J]. Journal of Tsinghua University, 2021, 61(6): 636–642 (in Chinese) [Google Scholar]
- CUIL, LUZ, HAOW. Importance analysis of the aircraft flap mechanism movement failure[J]. Journal of Aircraft, 2011, 48(2): 606–611 [Article] [CrossRef] [Google Scholar]
- MENGWei. Brief talks on the flap system of EMB145 regional jet airplanes[J]. Aviation Maintenance & Engineering, 2007, 1(1): 51 [Article] (in Chinese) [Google Scholar]
- BORELLOL, VILLEROG, DALLA VEDOVAM. New asymmetry monitoring techniques: effects on attitude control[J]. Aerospace Science and Technology, 2009, 13(8): 475–487 [Article] [CrossRef] [Google Scholar]
- ZUOPeng. Analysis and prevention of B737NG aircraft false trailing edge flap asymmetry[J]. Aviation Maintenance & Engineering, 2019(11): 78–80 [Article] (in Chinese) [Google Scholar]
- WANGMutian. Briefings of 737NG flap asymmetry shutdown fault and prevention measures[J]. Journal of Civil Aviation Flight University of China, 2019, 30(6): 41–43 [Article] (in Chinese) [Google Scholar]
- ZHANG Xiongfei. Research on fault diagnosis of retraction and extension of aircraft flap and slat based on QAR data[D]. Tianjin: Civil Aviation University of China, 2020 (in Chinese) [Google Scholar]
- MAChao, ZHANGXiongfei, XUJianxin. A risk prediction of aircraft flap asymmetry based on Monte Carlo method[J]. Journal of Transport Information and Safety, 2020, 38(3): 24–31 [Article] (in Chinese) [Google Scholar]
- ZHAOHongli, LIUYuwen. Forecasting for aero-engine failure risk based on Monte Carlo simulation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(3): 545–550 [Article] [Google Scholar]
- ZHUXiaowei, ZHAOHonghua, GOUJunzhe, et al. Research on performance predictive monitoring of B737NG aircrafttrailing edge flap disagree[J]. Aviation Maintenance & Engineering, 2019(1): 52–54 [Article] (in Chinese) [Google Scholar]
- JIABaohui, LIAOWenhui, LUXiang. Safety analysis for the landing gear structure on the basis of the non-probabilistic reliability theory[J]. Journal of Safety and Environment, 2021, 21(3): 1005–1011 [Article] (in Chinese) [Google Scholar]
- KESHTEGARB, BAGHERIM, FEIC W, et al. Multi-extremum-modified response basis model for nonlinear response prediction of dynamic turbine blisk[J]. Engineering with Computers, 2021, 38: 1243–1254 [Google Scholar]
- MAXiaojun, RENShuhong, ZUOHongfu, et al. Prediction method of aero-engine life on wing based on LS-SVM algorithm and performance reliability[J]. Journal of Traffic and Transportation Engineering, 2015, 15(3): 92–100 [Article] (in Chinese) [Google Scholar]
- CHENJ Y, FENGY W, TENGD, et al. Support vector machine-based similarity selection method for structural transient reliability analysis[J]. Reliability Engineering & System Safety, 2022, 223: 108513 [CrossRef] [Google Scholar]
- ZHOUD, ZHUANGX, ZUOH F. A hybrid deep neural network based on multi-time window convolutional bidirectional LSTM for civil aircraft APU hazard identification[J]. Chinese Journal of Aeronautics, 2022, 35(4344–361 [Article] [Google Scholar]
- FENGYunwen, PANWeihuang, LIUJiaqi, et al. Operational reliability of aircraft power plant based on machine learning[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(4): 394–404 (in Chinese) [Google Scholar]
- LIUJiaqi, FENGYunwen, LUCheng, et al. Safety analysis of aeroengine operation based on intelligent neural network[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(9): 136–147 (in Chinese) [Google Scholar]
- LUC, FENGY W, LIEMR P, et al. Improved Kriging with extremum response surface method for structural dynamic reliability and sensitivity analyses[J]. Aerospace Science and Technology, 2018, 76: 164–175 [CrossRef] [Google Scholar]
- TENGD, FENGY, LUC, et al. Novel Kriging-based decomposed-coordinated approach for estimating the clearance reliability of assembled structures[J]. Computer Modeling in Engineering & Sciences, 2021, 129(2): 1029–1049 [Google Scholar]
- WEIYifu, KAWAMURAYasumi, WANGDeyu. An improved moving least square method and application in structural reliability analysis[J]. Journal of Shanghai Jiaotong University, 2018, 52(4): 455–460 [Article] (in Chinese) [Google Scholar]
- FEIC W, LUC, LIEMR P. Decomposed-coordinated surrogate modeling strategy for compound function approximation in a turbine-blisk reliability evaluation[J]. Aerospace Science and Technology, 2019, 95: 105466 [CrossRef] [Google Scholar]
- LIX. Error estimates for the moving least-square approximation and the element-free Galerkin method in n-dimensional spaces[J]. Applied Numerical Mathematics, 2016, 99(1): 77–97 [Google Scholar]
- TENGD, FENGY W, CHENJ Y, et al. Structural dynamic reliability analysis: review and prospects[J]. International Journal of Structural Integrity, 2022, 13(5): 753–783 [CrossRef] [Google Scholar]
- ZHAND, XINGH. A fast Kriging-assisted evolutionary algorithm based on incremental learning[J]. IEEE Trans on Evolutionary Computation, 2021, 25(5): 941–955 [CrossRef] [Google Scholar]
- ZHAIX, FEIC W, CHOYY S, et al. A stochastic model updating strategy-based improved response surface model and advanced Monte Carlo simulation[J]. Mechanical Systems and Signal Processing, 2017, 82: 323–338 [CrossRef] [Google Scholar]
- FARAMARZIA, HEIDARINEJADM, STEPHENSB, et al. Equilibrium optimizer: a novel optimization algorithm[J]. Knowledge-Based Systems, 2020, 191: 105190 [Google Scholar]
- FEIC W, LIH, LUC, et al. Vectorial surrogate modeling method for multi-objective reliability design[J]. Applied Mathematical Modelling, 2022, 109: 1–20 [Google Scholar]
- TENGD, FENGY W, CHENJ Y. Intelligent moving extremum weighted surrogate modeling framework for dynamic reliability estimation of complex structures[J]. Engineering Failure Analysis, 2022, 138: 106364 [Google Scholar]
All Tables
All Figures
 |
图1 起飞阶段襟翼的工作状态 |
| In the text | |
 |
图2 基于CIMK的襟翼偏角可靠性分析流程 |
| In the text | |
 |
图3 分解协调策略原理示意图 |
| In the text | |
 |
图4 紧支撑区域获取有效样本的原理 |
| In the text | |
 |
图5 EO算法寻找最优紧支撑域半径过程示意图 |
| In the text | |
 |
图6 可靠度收敛分析 |
| In the text | |
 |
图7 襟翼偏角影响性分析柱状图 |
| In the text | |
 |
图8 影响概率分析 |
| In the text | |
 |
图9 基于测试样本的RSM、Kriging、SVM、BP-ANN与CIMK的绝对误差对比 |
| In the text | |
 |
图10 基于测试样本的RSM、Kriging、SVM、BP-ANN与CIMK的相对误差对比 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


