Computational and experimental research on the performance of ECRIT ion source with nitrogen propellant

Renwei TAN; Juan YANG; Hao MOU; Xianming WU

doi:10.1051/jnwpu/20234120274

All issues

Volume 41 / No 2 (April 2023)

JNWPU, 41 2 (2023) 274-281

Full HTML

Open Access

Issue		JNWPU Volume 41, Number 2, April 2023


Page(s)		274 - 281
DOI		https://doi.org/10.1051/jnwpu/20234120274
Published online		07 June 2023

JNWPU 2023, 41(2): 274–281

Computational and experimental research on the performance of ECRIT ion source with nitrogen propellant

氮工质ECRIT离子源性能计算与实验研究

Renwei TAN (谈人玮)¹, Juan YANG (杨涓)¹, Hao MOU (牟浩)¹ and Xianming WU (吴先明)²

¹ School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China
² Lanzhou Institute of Physics, Lanzhou 730000, China

Received: 8 June 2022

Abstract

Electron cyclotron resonance ion thruster (ECRIT) with a diameter of 2 cm has the characteristics of no hot cathode and high specific impulse, which is suitable for the air-breathing electric propulsion system. In order to adapt to the atmospheric composition characteristics of nitrogen and oxygen in low orbit, the computational and experimental research on the performance of the ECRIT ion sourse with nitrogen propellant is an important basis for analyzing the feasibility of applying ECRIT to the air-breathing electric propulsion system. In this paper, the global model of the nitrogen ECRIT ion source with a diameter of 2 cm is established to calculate its performance. Then, the computational results are compared with the experimental results to analyze the difference. The research results show that when the input power of the ion source is 8 W and the gas flow rate is 2 ml/min, the computational and experimental results of the extracted ion beam current and thrust reach the maximum with the extracted beam current of 16.2 and 12.5 mA and the thrust of 476.6 and 368 μN, respectively. When the input power is 8 W and the gas flow rate is 0.6 ml/min, the computational and experimental results of the specific impulse are 2 095.8 and 1 855.6 s, both reaching the maximum value. The relative errors between the computational and experimental results of the extracted ion beam current, thrust and specific impulse all range from 2% to 32%. When the input power and gas flow rate used are 8 W and 1 ml/min in calculation, and 8 W and 0.8 ml/min in experiment, the ion source is on the optimal operating state. At this situation, the computational and experimental propellant utilization efficiencies with 17.8% and 16.2% respectively are high, and the ion energy loss with 443.9 and 596.2 W/A respectively is low.

摘要

2 cm电子回旋共振离子推力器(electron cyclotron resonance ion thruster, ECRIT)具有无热阴极、比冲高等特点, 适用于吸气式电推进系统。为了适应低轨道氮氧混合大气成分特点, 开展氮工质ECRIT离子源的性能计算与实验研究, 是分析ECRIT应用于吸气电推进系统的可行性的重要基础。建立了氮工质2 cm ECRIT离子源的整体模型并计算其性能, 再与实验结果相互对比, 分析两者差别。研究结果表明: ①当离子源的输入功率为8 W, 气体流量为2 ml/min时, 离子引出束流和推力的计算与实验结果均达到最大值, 引出束流分别为16.2与12.5 mA, 推力分别476.6与368 μN。②当输入功率为8 W, 气体流量为0.6 ml/min时, 比冲的计算与实验结果为2 095.8与1 855.6 s, 均达到最大值, 离子引出束流、推力和比冲的计算与实验结果的相对误差变化范围均为2%~32%。③当计算采用的输入功率为8 W, 气体流量为1 ml/min, 实验采用的输入功率为8 W, 气体流量为0.8 ml/min时, 离子源都处于最优工作状态, 此时推进剂利用效率较高, 分别为17.8%和16.2%;离子能量损耗较低, 分别为443.9和596.2 W/A。

Key words: air-breathing electric propulsion / miniature ECR ion thruster / global model

关键字 : 吸气式电推进 / 微型ECR离子推力器 / 整体模型

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

低轨道航天器具有高观测精度, 因而被航天领域所关注。但是低轨道的大气阻力较大, 需要利用推进系统实现航天器的轨道保持。吸气式电推进系统能以低轨道稀薄大气作为工作介质, 无需推进剂供给系统, 具有寿命长、系统简单等优点[1-3]。电子回旋共振离子推力器(ECRIT)不依赖热阴极工作, 可用多介质推进剂工作, 适用于吸气式电推进系统。目前研究和应用比较成熟的有10 cm和2 cm氙工质ECRIT[4-5]。其中2 cm ECRIT结构紧凑、质量轻, 有用于低轨道微小卫星吸气式电推进系统的可能性。

对ECRIT离子源建立整体模型并开展性能计算, 再结合实验验证其准确性, 可以快速方便地评估ECRIT的性能。然而目前国内外在这方面的研究工作有限, 主要集中于氙气、水工质的ECRIT离子源性能评估。文献[6]对微型氙气和水工质ECRIT离子源进行了整体建模计算分析和实验研究, 计算与实验结果定性一致, 但是由于模型忽略等离子体分布、磁化效应以及鞘层结构, 计算与实验结果存在差异。在输入功率4~6 W的范围内, 水工质离子源的引出束流范围为11~18 mA, 相对误差范围为10%~40%;氙工质离子源的引出束流范围为8~12 mA, 相对误差范围为-25%~0%。文献[7]对10 cm氙工质ECRIT离子源进行了整体建模与性能计算, 发现电子携带能量大于3 eV时, 氙原子的电离性能最佳; 离子源长度的增加有利于提高推进剂利用效率; 栅极透明度的增加有利于降低放电损失, 但是会降低推进剂利用效率。这些研究工作说明利用整体模型评估离子源性能具有一定的准确性。文献[8]对2 cm氙工质ECRIT离子源进行了性能实验研究, 分析了离子引出束流随输入功率与气体流量的变化规律, 获得了最优的离子源结构。目前国内外以吸气式电推进为背景的2 cm ECRIT离子源的性能评估研究工作比较缺乏。上述研究工作虽然使用的氙气或水工质, 但是仍可以使用其中整理模型的构造方法以及实验方法开展氮工质的研究。

本文建立2 cm氮工质ECRIT离子源的整体模型, 通过求解能量、电流和质量守恒方程, 计算得到离子源的离子引出束流、推力、比冲等性能参数。通过实验研究, 获得离子源性能参数。通过计算与实验的对比, 分析计算与实验结果之间的差异和原因, 给出2 cm氮工质ECRIT离子源的最优工作状态。本文研究工作对于未来的低轨道飞行器吸气式电推力器的研究具有参考价值。

1 2 cm ECRIT离子源及其束流引出实验系统

1.1 2 cm ECRIT离子源

2 cm ECRIT的性能主要由离子源决定, 图1为其结构, 主要由内外磁环、磁轭、天线、圆柱腔体、屏栅和加速栅组成。离子源工作时, 电子在内外环形磁体形成的磁镜中做回旋运动。在电子回旋共振(electron cyclotron resonance, ECR)区, 电子回旋运动与微波电场等相位共振时, 电子被加热成高能电子, 并与中性粒子碰撞产生等离子体, 其中的离子通过屏栅和加速栅电势差引出并产生推力。

离子源的推力T、比冲I_sp、离子能量损耗ε_b和推进剂利用效率η_m由(1)~(4)式计算[9]

式中，I_b, U_b, P_i, P_r, M_g, ṁ_p和g分别是离子引出束流、离子加速电压、微波总功率、微波反射功率、氮分子质量、氮气质量流率和重力加速度。通过整体模型计算出离子引出束流后, 可以利用(1)~(4)式求出推力器的推力、比冲、离子能量损耗和推进剂利用效率, 由此得到性能的计算结果。如果以实验方法测得离子引出束流, 则可以利用上述公式获得推力、比冲、离子能量损耗和推进剂利用效率的实验值。性能的计算与实验结果相对比可以分析2种评估方法的差异。

图1

ECRIT离子源结构示意图

1.2 离子源束流引出实验系统

图2所示为2 cm ECRIT离子源束流引出实验系统图, 主要由离子源、真空舱、栅极电源、气体和微波传输线路组成。氮气和微波分别经气体和微波传输线路输入离子源, 其中微波频率为4.2 GHz。隔直器用于隔绝直流、通微波, 功率计用于测量从离子源反射出的微波功率P_r, 输入功率P_abs=P_i-P_r。推力器正常引出的离子束流I_b由屏栅电流I_s与加速栅截获电流I_a计算得到, I_b=I_s-I_a, 其中I_s=V_sr/R, I_a=V_ar/R, R是保护电阻阻值, R=3 000 Ω, V_sr和V_ar分别是屏栅和加速栅串联的保护电阻偏压。实验时控制屏栅电压V_s为1 500 V, 加速栅电压V_a为-350 V, 其中V_s=V_ss-V_sr, V_a=V_as-V_ar, V_ss和V_as分别为屏栅和加速栅的电源电压。离子加速电压U_b=V_s-V_a[9]。

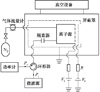图2

离子束流引出实验系统

2 离子源的整体建模及内部化学反应

2.1 整体建模

假设离子源内部等离子体近似为均匀分布, 根据能量、电流和质量守恒关系建立起来的方程组[6]即为整体模型。此模型综合了离子源的中性粒子密度、等离子体密度、鞘层电势降和电子温度之间的关系, 求解此模型可以得出离子源的离子引出束流随气体流量和输入功率的变化规律, 在此基础上利用(1)~(4)式可以理论计算评估推力、比冲、离子能量损耗和推进剂利用效率随气体流量和输入功率的变化规律, 并以最高的推进剂利用效率和最低的离子能量损耗为目标, 获得推力器的最佳工作参数, 即输入功率和气体流量[10]。

根据能量守恒关系, 输入功率与气体激发和电离反应消耗功率及壁面损失电荷和栅极引出电荷携带的功率相平衡, 即

式中：I_α和I_β分别为中性粒子单步激发和电离产生的等效电流；∈_α和∈_β分别为其对应的激发和电离势能; I_wi和I_we分别为壁面离子和电子电流损失; T_eV为电子温度; V_s为鞘层平均电势降[11]。

假设等离子体的径向分布均匀, 方程(5)中的I_α, I_β, I_wi, I_we和I_b分别由(6)~(10)式计算[12-13]

式中：n₀为中性粒子数密度, n₀=4ṁ_p(1-η_m)/[v₀(A_s+A_h)T_sη_cls][6], T_s为栅极有效透明度, η_cls为克劳辛系数; n_e为电子数密度; K_α和K_β分别为激发和电离反应速率常数, 由Bolsig+计算得到[14-15]; n_p为鞘层边界的等离子体密度, n_p=0.86·(3+0.5L_t/λ_i)n_i, L_t为离子源的特征长度, λ_i为离子的平均自由程, n_i为离子数密度; v_B为离子的波姆速度, 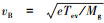; v_e为电子热速度, v_e=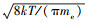, 气体温度T=300 K, m_e为电子质量; V为离子源体积; A_i为离子损失面积(包括屏栅及其孔和离子源内圆柱型壁面); A_e为电子损失面积(包括屏栅和磁环表面); A_s为屏栅面积; A_h为屏栅孔面积。

根据离子源电流守恒关系, 产生的离子电荷等效电流与壁面损失的离子电流和引出离子源的离子束流相等, 且等于等离子体的电子总电流, 即

根据质量守恒关系, 离子源输入气体流量等于泄露气体流量与反应消耗的气体流量之和, 即

式中, ṁ_q为流出推力器的氮分子质量流率。

在给定输入功率P_abs和气体流量ṁ_p的条件下, 由准中性条件n_i=n_e, 可利用模型中的方程(5)、(11)~(13)求解出中性粒子数密度n₀、离子数密度n_i、鞘层平均电势降V_s和电子温度T_eV共4个未知量, 并利用(10)式计算离子引出束流I_b, 从而根据(1)~(4)式评估推力器的性能。

2.2 化学反应

2 cm ECRIT离子源内的高能电子能量[16]只能使氮气分子电离为一价离子, 本文主要考虑的化学反应过程包括激发和电离反应, 共27步[17-18]。其中, 激发反应包括分子转动激发、分子振动激发和电子激发过程, 此处列出每个过程的一步主要反应

1) N₂+e^-→N₂(rot)+e^-, ∈_α=0.02 eV

2) N₂+e^-→N₂(v₁)+e^-, ∈_α=0.29 eV

3) N₂+e^-→N₂(B³)+e^-, ∈_α=7.35 eV

电离反应共有2步：

4) N₂+e^-→N₂⁺+2e^-, ∈_β=15.6 eV

5) N₂+e^-→N₂⁺(B² Σ)+2e^-, ∈_β=18.8 eV

化学反应提供了方程(5)中所需的反应势能∈、反应速率常数K和各项反应速率系数, 进而计算(6)和(7) 式中的等效电流。

3 基于计算和实验的氮工质2 cm ECRIT离子源性能

3.1 离子引出束流的计算与实验结果

利用前述整体模型, 根据2 cm ECRIT离子源的栅极的结构参数和透过率、离子损失面积等, 可以计算出不同输入功率和气体流量下离子源的离子引出束流。再通过离子源的离子束流引出实验得到不同输入功率和气体流量下的离子引出束流, 两者结果如图3所示。计算与实验结果表明, 在气体流量由0.6增大至2.2 ml/min过程中, 离子引出束流与输入功率和气体流量呈正相关, 这是因为输入功率增加使电子获能增加, 气体流量增加使中性粒子碰撞概率增加, 从而提高了气体电离率和等离子体密度, 增加了离子引出束流。但是气体流量的增加, 会引起离子源内的气体电离和离子引出过程相平衡, 使得等离子体密度不再变化, 离子引出束流达到饱和。不同输入功率下, 饱和离子束流的计算与实验结果如表1所示。对比计算与实验结果, 发现离子束流的计算值普遍高于实验值, 并且在低输入功率和低气体流量下的计算与实验结果最相近, 两者差异最小为2%;随着输入功率和气体流量的增大, 计算与实验结果的差异增加, 最大为32%。

分析其产生差异的原因如下: 当输入功率和气体流量较低时, 离子源内部的等离子体密度较低, ECR区和壁面附近区域的等离子体密度差异小, 使得计算结果和实验结果比较接近; 当输入功率和气体流量较高时, 离子源ECR区的等离子体密度较高, 等离子体自身的放电和漂移扩散过程产生的分布差异较明显, ECR区的等离子体密度大于壁面附近区域的等离子体密度, 等离子体密度分布存在不均匀性[19], 正是这种密度分布不均匀性引起了离子束流计算值的偏差。

图3

离子引出束流的计算与实验结果

表1

离子饱和束流的计算和实验评估

3.2 基于计算和实验的推力和比冲

基于3.1节离子引出束流的计算与实验结果, 利用(1)~(2)式对在不同输入功率和气体流量下的推力和比冲进行计算评估, 结果如图4所示。计算与实验结果表明, 在气体流量由0.6增大至2.2 ml/min过程中, 推力与输入功率和气体流量均呈正相关, 这是因为(1) 式中推力与离子引出束流呈正相关, 两者的变化规律相同; 比冲与输入功率呈正相关, 而与气体流量呈负相关, 这是因为(2) 式中当气体流量不变时, 比冲与推力呈正相关, 两者的变化规律相同, 而当气体流量改变时, 结合(1)、(2)和(4)式可知比冲与推进剂利用效率呈正相关, 气体流量的增加虽然会使中性粒子碰撞概率增加, 但同时也会加速电子能量的损失, 使得电离率减小, 推进剂利用效率减小, 从而比冲减小。不同输入功率下, 最大推力和比冲的计算与实验结果如表2和表3所示。推力和比冲的理论与实验结果差异与离子引出束流几乎一致, 最大达到32%, 最小可达2%。

图4

基于计算和实验的推力和比冲评估

表2

基于计算和实验的最大推力评估

表3

基于计算和实验的最大比冲评估

3.3 基于计算和实验的推进剂利用效率和离子能量损耗及最优工作参数

根据3.1节离子引出束流的计算与实验结果, 利用(3)和(4)式对在不同输入功率和气体流量下的推进剂利用效率和离子能量损耗进行计算评估, 结果如图5所示。计算与实验结果表明, 在气体流量由0.6增大至2.2 ml/min过程中, 推进剂利用效率和离子能量损耗都与输入功率呈正相关; 推进剂利用效率和离子能量损耗都与气体流量呈负相关。推进剂利用效率和离子能量损耗的理论与实验评估结果差异与离子引出束流几乎一致, 最大达到32%, 最小可达2%。离子源在不同输入功率下离子能量损耗与推进剂利用效率的关系曲线如图6所示, 可知当离子源输入功率不变时, 随着气体流量的减小, 计算与实验评估的离子能量损耗随着推进剂利用效率的增加, 均出现先缓慢增加后快速增加的现象; 当气体流量不变时, 随着离子源输入功率的增加, 理论与实验评估的离子能量损耗均随着推进剂利用效率的增加而缓慢增加。

一般情况下, 电推力器需要较高的推进剂利用效率和较低的离子能量损耗。当离子源输入功率不变时，随着气体流量的减小, 推进剂利用效率的增长率大于离子能量损耗增长率的临界点，即为需求的最优工作点。因此, 在图6上可以利用切线折中法[20], 以斜率为1的直线逼近图中各条曲线, 得到的切点即为离子源不同输入功率下的最优工作点, 对应点已于图中用虚线标出, 对应点性能参数的计算与实验评估结果如表4所示。当离子源处于最优工作状态时, 计算获得的输入功率为8 W、气体流量为1 ml/min、实验获得的输入功率为8 W、气体流量为0.8 ml/min。

由文献[21]可知, 低轨道大气阻力与轨道高度呈负相关, 与卫星迎风面积呈正相关, 12U(24 cm×24 cm×36 cm)立方星在200 km轨道工作时会产生约211 μN的大气阻力。由文献[2]可知, 假设推力器进气道气体捕获率达到50%时, 当其推进剂利用效率达到10%时, 可满足6U(10 cm×20 cm×30 cm)、12U、27U(34 cm×35 cm×35 cm)立方星在200 km轨道工作。假设只考虑氮气成分, 结合表4给出的离子源最优工作参数下推进剂利用效率的计算与实验评估结果, 推力均超过211 μN, 推进剂利用效率均达到10%, 可证明此推力器在立方星上的应用是可行的。

图5

基于计算和实验的推进剂利用效率和离子能量损失评估

图6

离子能量损失随推进剂利用效率的变化曲线

表4

在离子源最优运行参数下基于计算和实验的性能评估结果

4 结论

本文建立了2 cm ECRIT离子源的整体模型, 通过计算和实验研究, 评估了离子源的性能。得到的结论如下:

1) 2 cm氮工质ECRIT离子源离子引出束流计算与实验结果表明, 离子引出束流与输入功率和气体流量呈正相关, 最大离子引出束流的计算与实验结果分别为16.2和12.5 mA, 相对误差变化范围为2% ~ 32%, 整体模型中的电子均匀分布假设是导致计算与实验结果差异的主要原因。

2) 利用计算与实验得到的离子束流, 求得推力器的性能参数, 发现推力、比冲、推进剂利用效率和离子能量损耗均与输入功率呈正相关; 推力与气体流量呈正相关, 而比冲、推进剂利用效率和离子能量损耗均与气体流量呈负相关; 推力计算最大值为476.6 μN, 实验评估最大值为368 μN; 比冲计算最大值为2 095.8 s, 实验评估最大值为1 855.6 s, 各参数的相对误差变化范围也为2%~32%。

3) 根据离子能量损耗随推进剂利用效率的变化曲线, 利用切线折中法获取了各输入功率下离子源最优工作状态时的气体流量, 即输入功率分别为4, 6, 8 W时, 计算获得的最优气体流量分别为0.8, 1, 1 ml/min, 实验获得的最优气体流量均为0.8 ml/min, 其中输入功率为8 W时, 离子源的工作状态最优。这些工作参数均满足立方星吸气式推进系统的应用条件。

References

SERGE B, GIANLUCA C, RICCARDO A, et al. Conceptual design of an air-breathing electric propulsion system[C]//34th International Electric Propulsion Conference, 2015: 271–284 [Google Scholar]
JACKSON S W, MARSHALL R. Conceptual design of an air-breathing electric thruster for cubesat applications[J]. Journal of Spacecraft and Rockets, 2018, 55(3): 632–639 [Article] [NASA ADS] [CrossRef] [Google Scholar]
HU P, SHEN Y, YAO Z, et al. Study of multi-cusped plasma thruster applied to air-breathing electric propulsion[J]. Vacuum, 2021, 190: 110275–110281 [Article] [CrossRef] [Google Scholar]
TSUKIZAKI R, ISE T, KOIZUMI H, et al. Thrust enhancement of a microwave ion thruster[J]. Journal of Propulsion and Power, 2014, 30(5): 1383–1389 [Article] [CrossRef] [Google Scholar]
KOIZUMI H, KUNINAKA H. Performance of the miniature and low power microwave discharge ion engine μ1[C]//46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, 2010: 6617-6623 [Google Scholar]
NAKAGAWA Y, KOIZUMI H, NAITO Y, et al. Water and xenon ECR ion thruster-comparison in global model and experiment[J]. Plasma Sources Science and Technology, 2020, 29(10): 105003–105020 [Article] [Google Scholar]
WANG Yuquan, YANG Juan, JIN Yizhou, et al. Calculation and analysis of ECRIT ion source performance based on Geobel model[J]. Mechanical Science and Technology for Aerospace Engineering, 2017, 36(5): 749–754 [Article] (in Chinese) [Google Scholar]
XIA Xu, YANG Juan, JIN Yizhou, et al. Experimental study on the effect of magnetic circuit and antenna position on the performance of 2 cm electron cyclotron resonance ion thruster[J]. Acta Physica Sinica, 2019, 68(23): 230–240 (in Chinese) [Google Scholar]
HUANG Yizhi. Experimental study on xenon working medium micro-thrust ECR ion thruster[D]. Xi'an: Northwestern Polytechnical University, 2018 (in Chinese) [Google Scholar]
GRONDEIN P, LAFLEUR T, CHABERT P, et al. Global model of an iodine gridded plasma thruster[J]. Physics of Plasmas, 2016, 23(3): 033514–033523 [Article] [NASA ADS] [CrossRef] [Google Scholar]
HURLBATT A, GIBSON A R, SCHRÖTER S, et al. Concepts, capabilities, and limitations of global models: a review[J]. Plasma Processes and Polymers, 2017, 14(1/2): 1600138–1600158 [Google Scholar]
LIEBERMAN M A, LICHTENBERG A J. Principles of plasma discharges and materials processing[D]. New Jersey: John Wiley & Sons, 2005 [CrossRef] [Google Scholar]
DAN M G, IRA K. Fundamentals of electric propulsion: Ion and hall thrusters[M]. New Jersey: John Wiley & Sons, 2008 [Google Scholar]
HAGELAAR G J M, PITCHFORD L C. Solving the boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models[J]. Plasma Sources Science and Technology, 2005, 14(4): 722–733 [Article] [Google Scholar]
HIGURASHI Y, OHNISHI J, NAKAGAWA T, et al. Results of RIKEN superconducting electron cyclotron resonance ion source with 28 GHz[J]. Review of Scientific Instruments, 2012, 83(2): 02A [Google Scholar]
XIA X, YANG J, JIN Y Z, et al. The influence of magnetic circuit and operating parameters on the plasma property of 2 cm ECRIT ion source[J]. Vacuum, 2020, 179: 109517–109523 [Article] [CrossRef] [Google Scholar]
BOSI F, TREZZOLANI F, LUCCA FABRIS A, et al. Modelling and optimization of electrodeless helicon plasma thruster with different propellants[C]//50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, 2014: 3404-3420 [Google Scholar]
PITCHFORD L, BORDAGE M C, HAGELAAR G, et al. Comparisons of sets of electron-neutral scattering cross sections and calculated swarm parameters in O₂[J]. Berichte Der Bunsengesellschaft Für Physikalische Chemie, 2012, 93(5): 580–585 [Google Scholar]
XIA X, YANG J, FU Y L, et al. Numerical simulation of influence of magnetic field on plasma characteristics and surface current of ion source of 2 cm electron cyclotron resonance ion thruster[J]. Acta Physica Sinica, 2021, 70(7): 075204–075211 [Article] [Google Scholar]
WANG Yuquan, CHEN Xiaolong, YANG Juan. Calculation evaluation of variable thrust performance of 10 cm ECR ion thruster[J]. Journal of northwestern polytechnical university, 2017, 35(3): 448–454 [Article][Article] (in Chinese) [Google Scholar]
JACKSON S W. Design of an air-breathing electric thruster for CubeSat applications[D]. Boulder: University of Colorado, 2017 [Google Scholar]

All Tables

离子饱和束流的计算和实验评估

基于计算和实验的最大推力评估

基于计算和实验的最大比冲评估

在离子源最优运行参数下基于计算和实验的性能评估结果

In the text

All Figures

	图1 ECRIT离子源结构示意图
In the text

	图2 离子束流引出实验系统
In the text

	图3 离子引出束流的计算与实验结果
In the text

	图4 基于计算和实验的推力和比冲评估
In the text

	图5 基于计算和实验的推进剂利用效率和离子能量损失评估
In the text

	图6 离子能量损失随推进剂利用效率的变化曲线
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] SERGE B, GIANLUCA C, RICCARDO A, et al. Conceptual design of an air-breathing electric propulsion system[C]//34th International Electric Propulsion Conference, 2015: 271–284 [Google Scholar]

[2] JACKSON S W, MARSHALL R. Conceptual design of an air-breathing electric thruster for cubesat applications[J]. Journal of Spacecraft and Rockets, 2018, 55(3): 632–639 [Article] [NASA ADS] [CrossRef] [Google Scholar]

[3] HU P, SHEN Y, YAO Z, et al. Study of multi-cusped plasma thruster applied to air-breathing electric propulsion[J]. Vacuum, 2021, 190: 110275–110281 [Article] [CrossRef] [Google Scholar]

[4] TSUKIZAKI R, ISE T, KOIZUMI H, et al. Thrust enhancement of a microwave ion thruster[J]. Journal of Propulsion and Power, 2014, 30(5): 1383–1389 [Article] [CrossRef] [Google Scholar]

[5] KOIZUMI H, KUNINAKA H. Performance of the miniature and low power microwave discharge ion engine μ1[C]//46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, 2010: 6617-6623 [Google Scholar]

[6] NAKAGAWA Y, KOIZUMI H, NAITO Y, et al. Water and xenon ECR ion thruster-comparison in global model and experiment[J]. Plasma Sources Science and Technology, 2020, 29(10): 105003–105020 [Article] [Google Scholar]

[7] WANG Yuquan, YANG Juan, JIN Yizhou, et al. Calculation and analysis of ECRIT ion source performance based on Geobel model[J]. Mechanical Science and Technology for Aerospace Engineering, 2017, 36(5): 749–754 [Article] (in Chinese) [Google Scholar]

[8] XIA Xu, YANG Juan, JIN Yizhou, et al. Experimental study on the effect of magnetic circuit and antenna position on the performance of 2 cm electron cyclotron resonance ion thruster[J]. Acta Physica Sinica, 2019, 68(23): 230–240 (in Chinese) [Google Scholar]

[9] HUANG Yizhi. Experimental study on xenon working medium micro-thrust ECR ion thruster[D]. Xi'an: Northwestern Polytechnical University, 2018 (in Chinese) [Google Scholar]

[10] GRONDEIN P, LAFLEUR T, CHABERT P, et al. Global model of an iodine gridded plasma thruster[J]. Physics of Plasmas, 2016, 23(3): 033514–033523 [Article] [NASA ADS] [CrossRef] [Google Scholar]

[11] HURLBATT A, GIBSON A R, SCHRÖTER S, et al. Concepts, capabilities, and limitations of global models: a review[J]. Plasma Processes and Polymers, 2017, 14(1/2): 1600138–1600158 [Google Scholar]

[12] LIEBERMAN M A, LICHTENBERG A J. Principles of plasma discharges and materials processing[D]. New Jersey: John Wiley & Sons, 2005 [CrossRef] [Google Scholar]

[13] DAN M G, IRA K. Fundamentals of electric propulsion: Ion and hall thrusters[M]. New Jersey: John Wiley & Sons, 2008 [Google Scholar]

[14] HAGELAAR G J M, PITCHFORD L C. Solving the boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models[J]. Plasma Sources Science and Technology, 2005, 14(4): 722–733 [Article] [Google Scholar]

[15] HIGURASHI Y, OHNISHI J, NAKAGAWA T, et al. Results of RIKEN superconducting electron cyclotron resonance ion source with 28 GHz[J]. Review of Scientific Instruments, 2012, 83(2): 02A [Google Scholar]

[16] XIA X, YANG J, JIN Y Z, et al. The influence of magnetic circuit and operating parameters on the plasma property of 2 cm ECRIT ion source[J]. Vacuum, 2020, 179: 109517–109523 [Article] [CrossRef] [Google Scholar]

[17] BOSI F, TREZZOLANI F, LUCCA FABRIS A, et al. Modelling and optimization of electrodeless helicon plasma thruster with different propellants[C]//50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, 2014: 3404-3420 [Google Scholar]

[18] PITCHFORD L, BORDAGE M C, HAGELAAR G, et al. Comparisons of sets of electron-neutral scattering cross sections and calculated swarm parameters in O₂[J]. Berichte Der Bunsengesellschaft Für Physikalische Chemie, 2012, 93(5): 580–585 [Google Scholar]

[19] XIA X, YANG J, FU Y L, et al. Numerical simulation of influence of magnetic field on plasma characteristics and surface current of ion source of 2 cm electron cyclotron resonance ion thruster[J]. Acta Physica Sinica, 2021, 70(7): 075204–075211 [Article] [Google Scholar]

[20] WANG Yuquan, CHEN Xiaolong, YANG Juan. Calculation evaluation of variable thrust performance of 10 cm ECR ion thruster[J]. Journal of northwestern polytechnical university, 2017, 35(3): 448–454 [Article][Article] (in Chinese) [Google Scholar]

[21] JACKSON S W. Design of an air-breathing electric thruster for CubeSat applications[D]. Boulder: University of Colorado, 2017 [Google Scholar]