| Issue |
JNWPU
Volume 42, Number 1, February 2024
|
|
|---|---|---|
| Page(s) | 62 - 69 | |
| DOI | https://doi.org/10.1051/jnwpu/20244210062 | |
| Published online | 29 March 2024 | |
Microscopic morphology modeling and prediction of flexible polished surface with belt flapwheel
砂布页轮柔性抛光表面微观形貌建模与预测
1
School of Mechanical Engineering, Xi’an Aeronautical University, Xi’an 710077, China
2
School of Intelligent Manufacturing and Control Technology, Xi’an Mingde Institute of Technology, Xi’an 710124, China
3
School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China
Received:
15
January
2023
Flexible polishing technology is widely used in the precision machining of aero-engine blisk blades. It has become one of the important research contents of flexible polishing technology to systematically study the flexible polishing process and understand the connotation of the microscopic morphology of the polished surface. In this paper, the flapwheel is used as a flexible abrasive tool, and the spatial kinematics model for the abrasive grains on the surface of the flapwheel and the geometric interference model for the abrasive grains and workpiece are established by transforming the spatial geometric coordinates. Based on the surface topography model for the abrasive tool, MATLAB software was used to simulate the micro topography generation process of the flexible polishing surface with flapwheel as abrasive tool, and the three-dimensional topography of the workpiece surface and its influence law under different process parameters were obtained. The polishing experimental results verified the simulation algorithm correctness and effectiveness.
摘要
柔性抛光技术广泛应用于航空发动机整体叶盘叶片的精密加工。系统深入研究柔性抛光过程, 了解抛光加工表面微观形貌生成的内涵, 成为柔性抛光加工技术的重要研究内容之一。以砂布页轮为柔性磨具, 通过空间几何坐标变换建立了砂布页轮表面磨粒的空间运动学模型及磨粒-工件几何学干涉模型, 并研究了砂布页轮柔性变形对工件表面磨粒运动轨迹的影响。基于磨具表面形貌模型, 利用MATLAB软件进行砂布页轮柔性抛光表面微观形貌生成过程仿真, 并得到不同工艺参数下工件表面三维形貌及其影响规律, 抛光实验结果验证了该仿真算法的正确性和有效性。
Key words: blisk blade / flexible polishing / spatial geometry coordinate conversion / surface microtopography
关键字 : 整体叶盘叶片 / 柔性抛光 / 空间几何坐标转换 / 表面微观形貌
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
整体叶盘作为航空发动机的关键重要结构件, 其表面质量影响整机使用性能和寿命[1]。整体叶盘的叶片弯扭、薄壁且长, 叶片之间相互遮掩、通道狭窄、开敞性差, 这些结构特点使得磨具系统可达性差, 在抛光过程中磨具极易与叶片的叶尖部位及进排气边发生干涉。而柱状类柔性磨具, 如砂布页轮、砂圈、芝麻磨头等, 因结构简单、具有更好的可达性, 适合开敞性差的整体叶盘叶片抛光加工[2]。而抛光表面形貌是由磨粒随磨具运动并与工件相互作用而生成的。在已获得磨具表面磨粒分布特征的基础上[3], 通过对抛光过程中的磨粒与工件间的运动关系进行建模, 了解抛光表面微观形貌生成过程, 对控制和提高抛光表面质量具有重要意义[4]。
随着计算机技术的发展, 可在计算机的帮助下对被加工零件的三维表面进行数字化仿真[5]。Wang等[6]将叶片磨削过程中非线性时变接触接触变形规律叠加在磨粒运动轨迹方程上, 准确地获得磨削点的空间位置, 并通过工件形貌生成算法获得了不同曲率变化下的加工表面粗糙度。He等[7]采用塑性有限元法模拟单颗磨粒抛光过程, 根据叶片砂带抛光特点确定了仿真加工方式, 通过模拟不同抛光参数下的抛光过程, 得到不同抛光参数下单颗磨粒抛光力变化曲线。Chen等[8]考虑磨粒的不同突出高度、砂轮形状和工具的微振动, 将微观的磨粒空间运动学和宏观的砂轮高频振动相联系, 建立了多尺度模型并研究磨粒轨迹对磨削工件表面质量的影响。孙聪等[9]将可靠性分析引入到颤振研究中, 并将动力学特性耦合到磨削形貌仿真模型中, 讨论了砂轮磨削参数和动力学参数对磨粒轨迹的影响。陈海峰等[10]将磨粒参与磨削深度定义为随时间变化的实时切削深度, 建立未变形切屑的截面积与实时切削深度之间的关系, 继而通过模拟所有磨粒的三维切削轨迹并去除干涉材料,从而生成表面形貌[10]。
综上研究可知, 通过建立磨具和工件之间的相互作用关系, 可进行数字化仿真构建抛光表面形貌模型。基于此, 本文以砂布页轮为抛光柔性磨具, 根据空间几何坐标变换原理和矢量运算规则, 推导出砂布页轮抛光工件过程中磨具表面磨粒与工件干涉时的切削轨迹方程, 利用MATLAB软件进行砂布页轮柔性抛光表面微观形貌生成仿真并进行实验验证, 从而分析砂布页轮柔性抛光表面微观形貌生成机理, 揭示工艺参数对抛光表面形成影响规律。
1 磨粒空间运动学模型
了解磨具表面磨粒的空间运动, 是对磨粒与工件之间的运动学相互作用进行建模和对工件抛光表面微观形貌进行预测的基础。在复杂曲面叶片的抛光加工中涉及到多种空间运动, 如磨粒随磨具做圆周回转运动、机床主轴位姿偏转、空间进给运动。其空间几何坐标系转换主要为直角坐标系的平移和旋转2种转换。为了准确描述磨具表面磨粒的空间运动, 建立如图 1所示的抛光加工坐标系。本文研究内容以建立抛光表面微观形貌模型为主, 为了减少仿真运算时间以及降低复杂曲面叶片型面的曲率变化对抛光形貌的影响, 以小尺寸平板零件为抛光工件进行建模, 且进给路径均设置为直线进给。
如图 1所示, 在砂布页轮抛光工件过程中, 磨粒运动对工件的切削作用依次涉及到如下空间运动转换: 磨粒随磨具做圆周运动、磨具绕磨头主轴做偏心回转运动、磨头主轴位姿调整以及相对于工件的进给运动。抛光加工过程涉及到如下3个空间坐标系:
1) 磨具坐标系OT-UVW。随磨具一起做偏心回转运动, 不随磨具做圆周运动, 其坐标系原点通过磨具轴线。
2) 主轴坐标系OM-U′V′W′。随主轴做位姿调整和相对于工件的进给运动。其中坐标系穿过主轴轴线, 转动轴V′平行于V, U′-OM-W′平行于磨具端面U-OT-W。回转偏心振幅为0时, 主轴坐标系OM-U′V′W′与磨具坐标系OT-UVW重合。
3) 工件坐标系OW-XYZ。固定在工件上, 坐标原点为工件边角某一点, X轴正方向与进给方向相一致。
根据空间几何坐标变换原则[11], 由坐标系O-XYZ到坐标系O′-X′Y′Z′的坐标变换如(1)式所示。
式中,(x′0, y′0, z′0)为坐标系O-XYZ的坐标原点O在坐标系O′-X′Y′Z′中的坐标; θij为坐标系O′-X′Y′Z′中3个坐标轴X′, Y′, Z′中的第i轴与坐标系O-XYZ中3个坐标轴X, Y, Z中的第j轴之间夹角。
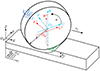 |
图1 抛光加工空间坐标系 |
1.1 磨具坐标系下的磨粒切削刃方程
基于构建的磨具表面形貌仿真模型[12], 可先根据所需磨具尺寸生成一定尺寸范围的静态磨具表面形貌高度矩阵。设砂布页轮公称半径为r, 宽度为W, 则磨具表面形貌仿真模型生成展开矩形区域尺寸为2πr×W的静态磨具表面形貌磨粒出刃高度矩阵 h (i, j)。长度l方向和宽度k方向分别按间隔lx-grid和ly-grid离散为m+1和n+1个点, 其中lx-grid×m=2πr, ly-grid×n=W。则磨粒切削刃上任意点G的高度为 h (i, j)(i=0, 1, 2, 3, …, m; j=0, 1, 2, 3, …, n)。
将展开的磨具表面形貌h(i, j)覆盖于圆柱磨具表面, 如图 2所示, 设磨具表面磨粒分布不随圆周运动而变化, 某磨粒切削刃的圆周运动半径R, 主轴转速为n, 初始角为α0, 则t时刻磨粒切削刃上任意点G在磨具坐标系OT-UVW中的运动轨迹如(2)式所示。
式中,R=r+ h (i, j), α0=i/m×2π(rad)。
以上为假定静态砂布页轮表面形貌在不随圆周运动而变化情况下, 得到的磨具坐标系下磨粒切削刃轨迹方程。实际计算时, 砂布页轮会随着圆周运动变化运动半径R, 且随着砂布页轮受压缩程度的不同而不断更新动态表面形貌[12]。
 |
图2 磨具表面磨粒的圆周运动 |
1.2 主轴坐标系下的磨粒切削刃方程
由于砂布页轮中心胶体上的螺纹孔、用于连接磨具和磨头主轴刀柄的连杆以及机床本身, 均存在一定程度的制造偏差, 从而造成磨具在圆周运动过程中发生一定程度的运动偏差, 使得磨具坐标系OT-UVW与机床主轴坐标系OM-U′V′W′不重合。设磨具的回转偏心振幅为Δdrad, 则磨具坐标系原点OT在磨头主轴坐标系OM-U′V′W′的坐标如(3)式所示。
则时刻t磨具表面切削刃任意点G由磨具坐标系OT-UVW到主轴坐标系OM-U′V′W′的转换矩阵如(4)式所示。
则磨具圆周运动过程中磨粒切削刃任意点G在主轴坐标系OM-U′V′W′下的坐标如(5)式所示。
1.3 工件坐标系下的磨粒切削刃方程
设磨具相对工件的进给速度为vf, 则主轴坐标系OM-U′V′W′原点OM在工件坐标系OW-XYZ的坐标如(6)式所示。
对于整体叶盘叶片类复杂曲面零件, 叶片长且叶片间通道狭窄, 在抛光加工过程中可适当调整主轴位姿,在叶片表面偏转一定角度以避免连杆与叶尖、进排气边发生干涉。即在五轴机床抛光整体叶盘叶片过程中, 同时存在磨具-工件的相对进给运动和主轴位姿偏转。为了简化研究, 本部分假设铣削纹路方向与工件长度方向相同, 仅针对平面工件抛光过程中主轴位姿在工件平面上偏转角度θ, 并沿着工件长度方向进给的抛光方式进行研究, 如图 1所示。抛光中, 主轴坐标系OM-U′V′W′到工件坐标系OW-XYZ的旋转转换矩阵如(7)式所示。
而主轴坐标系OM-U′V′W′到工件坐标系OW-XYZ的旋转转换矩阵如(8)式所示。
综上, 可得磨具表面磨粒切削刃任意一点G在工件坐标系OW-XYZ的坐标如公式(9)所示。
2 抛光表面微观形貌仿真
磨粒切削工件材料的塑性变形对抛光表面创成起决定性的作用。目前, 大多数表面创成仿真算法仅考虑了磨粒的切削作用; 而磨粒的耕犁作用使得工件材料在磨粒两侧隆起, 高于初始表面。抛光过程中, 磨粒的切削作用和耕犁作用使得工件表面材料既有切削去除, 又有耕犁隆起。考虑到参与抛光过程的磨粒数量多、切削次数多, 因此, 抛光表面创成过程更为复杂。本文将同时考虑磨粒的切削作用和耕犁作用, 对抛光表面微观形貌生成过程进行研究。
2.1 磨粒与工件几何学干涉模型
在抛光过程中, 柔性磨具表面的磨粒与工件接触, 磨具受工件挤压, 磨粒位置被抬升, 从而使磨粒与工件之间的实际干涉曲线高于理论值。在构建的砂布页轮表面形貌模型中[8], 磨具受挤压后磨粒在工件表面的运动轨迹被简化为圆周运动, 通过将运动半径为Rn的砂布页轮等效为运动半径为Rt的砂布页轮从而建立动态砂布页轮表面形貌模型。而砂布页轮作为涂附磨具, 砂布页片自身具有一定的柔性, 即使承载磨粒运动的基体不发生柔性变形, 磨粒运动在与工件干涉时, 也会因砂布页片布基材料和涂附胶体的柔性而发生运动轨迹的变化, 磨粒运动轨迹有一定程度抬升, 切入工件的深度小于理论切入深度。因此, 可将砂布页轮抛光中由于磨具柔性而与工件干涉区域的磨粒运动轨迹变化分为两部分: 一部分为磨具柔性变形引起的宏观磨粒运动轨迹变化(宏观弹性变形); 另一部分为涂附磨具自身柔性而引起的微观磨粒运动轨迹变化(微观弹性变形)。其中, 因磨具柔性变形引起的宏观磨粒运动可采用等效运动半径Rt的动态砂布页轮表面磨粒在工件坐标系下的磨粒运动方程表述。
2.2 抛光表面微观形貌仿真过程
1) 建立工件表面微观结构矩阵
抛光表面形貌由磨具表面无数磨粒在工件表面的切削痕迹累加所形成。通过对比每颗磨粒的切削痕迹高度和工件表面高度, 以及磨粒切削工件的塑性变形轮廓, 即可获得抛光表面形貌。根据所需密度, 在工件坐标系OW-XYZ中将工件表面用m×n个网格点进行划分。工件表面任何点的高度设置为zij。
2) 数值形貌生成过程
由于磨粒滑擦作用仅使工件材料发生弹性变形, 不影响抛光表面形貌的生成, 在仿真算法中忽略滑擦作用且忽略工件材料的弹性变形; 同时考虑耕犁作用和切削作用, 以截面轮廓的材料堆积率量化工件材料的塑性变形, 且其材料堆积率小于塑性变形有限元仿真中不考虑材料去除情况下得到的材料堆积率。由于磨粒尺寸和切削深度对塑性变形的影响最大, 而切削速度对塑性变形的影响较小, 为了简化计算过程, 对不同粒度的磨粒分别设置最大切深时的材料堆积率(P240为0.5, P320为0.45, P400为0.35)。
综合有关磨粒的运动和特征理论, 砂布页轮抛光平板工件过程的整个表面形貌仿真过程如下: 首先输入抛光工艺仿真参数, 并初始化仿真过程; 然后加载静态砂布页轮表面形貌数据;根据磨粒空间运动学模型、磨粒与工件几何干涉学模型, 求解由磨粒运动产生的工件表面形貌矩阵, 并更新工件的表面形貌矩阵; 重复循环上述程序部分, 直到磨具离开工件表面, 即磨粒运动不再与工件干涉; 最后输出工件表面形貌矩阵。根据以上建立的磨粒空间运动学模型、磨粒与工件几何干涉学模型, 用MATLAB编程语言对砂布页轮抛光过程进行编程, 通过数值模拟实现对抛光表面微观形貌生成过程的仿真分析。
3 工艺参数对表面微观形貌的影响
3.1 主轴转速对抛光表面微观形貌的影响
设置压缩量ap为0.5 mm, 进给速度vf为300 mm/min, 磨具回转偏心振幅43 μm, 进行横向抛光工艺下P320砂布页轮在主轴转速n为5 000, 6 000, 7 000, 8 000 r/min时的抛光表面微观形貌仿真和TC4平板(60 mm×90 mm×20 mm)抛光实验。抛光后用Mahr MarSurf M300C手持式粗糙度测量仪测量表面粗糙度值, 每次抛光后随机测量5个区域并测量3次, 取其平均值作为最终的粗糙度值。测量方向为垂直于磨粒切削方向。对不同主轴转速砂布页轮抛光仿真和抛光实验的表面形貌进行表面粗糙度统计结果如图 3所示。利用Infinite Focus G4自动变焦三维表面测量仪, 观测最低与最高主轴转速下抛光实验获得的表面形貌如图 4所示, 相应加工参数的抛光加工形貌仿真获得的表面形貌如图 5所示。
 |
图3 抛光表面粗糙度随主轴转速n的变化 |
 |
图4 不同转速n下砂布页轮抛光实验的工件表面形貌 |
 |
图5 不同转速n下砂布页轮抛光表面形貌仿真 |
3.2 进给速度对抛光表面微观形貌的影响
设置主轴转速n为6 000 r/min、压缩量ap为0.6 mm, 磨具回转偏心振幅为34 μm, 进行横向抛光工艺下P320砂布页轮在进给速度vf为200, 300, 400, 500 mm/min条件下的抛光表面创成微观形貌仿真。对不同进给速度砂布页轮抛光仿真和抛光实验的表面形貌分别进行表面粗糙度统计, 结果如图 6所示。利用Infinite Focus G4自动变焦三维表面测量仪, 观测最低与最高进给速度下抛光实验获得的表面形貌如图 7所示, 相应加工参数的抛光加工形貌仿真获得的表面形貌如图 8所示。
 |
图6 抛光表面粗糙度随进给速度vf的变化 |
 |
图7 不同进给速度vf下砂布页轮抛光实验的工件表面形貌 |
 |
图8 不同进给速度vf下砂布页轮抛光表面形貌仿真 |
3.3 前倾角对抛光表面微观形貌的影响
设置主轴转速n为7 000 r/min, 压缩量ap为0.5 mm, 进给速度vf为400 mm/min, 磨具回转偏心振幅为45 μm, 进行P400粒度砂布页轮在前倾角θ为0°,10°,20°,30°条件下的抛光微观形貌仿真和TC4平板抛光实验。对不同前倾角抛光工艺下的砂布页轮抛光仿真和抛光实验的表面形貌进行表面粗糙度统计如图 9所示。利用Infinite Focus G4自动变焦三维表面测量仪, 观测最小与最大前倾角抛光工艺下的抛光实验获得的表面形貌, 如图 10所示, 相应加工参数的抛光加工形貌仿真获得的表面形貌如图 11所示。
从图 9~11可以看出, 抛光表面粗糙度随前倾角的增大而减小。从工件表面纹理可以看出, 宏观上表面纹理的方向与进给方向相同, 而微观上磨粒的切削轨迹方向与前倾角方向相同。从机理上分析, 对于前倾角为0°的横向抛光工艺, 磨粒的切削方向与进给方向相同, 抛光加工参数极易影响其抛光表面质量; 而随着前倾角增加的前倾抛光工艺, 磨粒切削方向不再与进给方向相同, 磨粒空间的运动轨迹也更为复杂, 从而影响加工表面形貌, 使得抛光表面粗糙度下降。
 |
图9 抛光表面粗糙度随前倾角θ的变化 |
 |
图10 不同前倾角θ下抛光工艺砂布页轮抛光实验的工件表面形貌 |
 |
图11 不同前倾角θ下抛光工艺的砂布页轮抛光表面形貌仿真 |
4 结论
本文通过空间几何坐标变换建立了砂布页轮表面磨粒的空间运动学模型, 并研究了砂布页轮柔性变形对工件表面磨粒运动轨迹的影响。基于已建立的磨具表面形貌模型, 利用MATLAB软件进行砂布页轮柔性抛光表面微观形貌生成仿真, 并研究了工艺参数对抛光表面微观形貌的影响规律, 得出以下结论:
1) 抛光实验结果验证了基于MATLAB软件进行砂布页轮柔性抛光表面微观形貌建模的正确性和有效性;
2) 抛光表面粗糙度随主轴转速、前倾角的增加而减小, 随进给速度的增加而增大;
3) 砂布页轮柔性抛光中, 在选定磨具参数、加工参数固定不变的前提下, 通过变化刀轴位姿的前倾抛光工艺进行抛光即可降低抛光表面粗糙度, 提高表面质量。因此, 需要对前倾抛光工艺影响抛光表面创成的作用机制进行进一步研究。
References
- LIWenhui, WENXuejie, LIXiuhong, et al. Research status and development trend of blisk polishing technology[J]. Aeronautical Manufacturing Technology, 2022, 65(17): 88–102 [Article](in Chinese) [Google Scholar]
- ZHANG Junfeng, WU Xiaojun, SHI Yaoyao, et al. Research on modeling of material removal depth for blisk polishing by abrasive belt flap wheel based on hertz contact theory[J]. China Mechanical Engineering, 2022, 6: 1–10 [Article](in Chinese) [Google Scholar]
- ANANDITA S, MOTE R G, SINGH R. Surface generation via scallop overlap analysis during grinding[J]. The International Journal of Advanced Manufacturing Technology, 2019, 100(5/6/7/8): 1193–1206 [CrossRef] [Google Scholar]
- WANG Lei. Research on surface roughness of tibw mesh reinforced titanium matrix composites by ultrasonic vibration grinding[D]. Harbin: Harbin Institute of Technology, 2021 (in Chinese) [Google Scholar]
- YAN Zezhao, LI Wenhui, LI Xiuhong, et al. Simulation and comparative analysis of different mass finishing for aeroengine blisk parts[J]. Modular Machine Tool & Automatic Manufacturing Technique, 20221): 138–143 [Article](in Chinese) [Google Scholar]
- WANG T, ZOU L, WAN Q, et al. A high-precision prediction model of surface roughness in abrasive belt flexible grinding of aero-engine blade[J]. Journal of Manufacturing Processes, 2021, 66: 364–375 [Article] [CrossRef] [Google Scholar]
- HE Q W, SUN S, WANG X, et al. Research on simulation of abrasive belt polishing process for blade finishing[C]//The 2nd International Workshop on Materials Science and Mechanical Engineering, 2019 [Google Scholar]
- CHEN S, CHEUNG C F, ZHANG F, et al. Three-dimensional modelling and simulation of vibration marks on surface generation in ultra-precision grinding[J]. Precision Engineering, 2018, 53: 221–235 [CrossRef] [Google Scholar]
- SUN C, DENG Y, LAN D, et al. Modeling and predicting ground surface topography on grinding chatter[C]//4th CIRP Conference on Surface Integrity, 2018: 364–369 [Google Scholar]
- CHEN Haifeng, TANG Jinyuan, DENG Zhaohui, et al. Modeling and predicting surface topography of the ultrasonic assisted grinding process considering ploughing action[J]. Journal of Mechanical Engineering, 2018, 54(21): 231–240 [Article](in Chinese) [CrossRef] [Google Scholar]
- KANG Ning. Research on milling force modeling and manufacturing process of TC4 titanium[D]. Shenyang: Northeastern University, 2019 (in Chinese) [Google Scholar]
- CHEN Zhen, YAN Rui, LI Feng, et al. Surface morphology measurement and modeling of belt flapwheel[J]. Aeronautical Manufacturing Technology, 2022, 65(4): 6372 [Article](in Chinese) [Google Scholar]
All Figures
 |
图1 抛光加工空间坐标系 |
| In the text | |
 |
图2 磨具表面磨粒的圆周运动 |
| In the text | |
 |
图3 抛光表面粗糙度随主轴转速n的变化 |
| In the text | |
 |
图4 不同转速n下砂布页轮抛光实验的工件表面形貌 |
| In the text | |
 |
图5 不同转速n下砂布页轮抛光表面形貌仿真 |
| In the text | |
 |
图6 抛光表面粗糙度随进给速度vf的变化 |
| In the text | |
 |
图7 不同进给速度vf下砂布页轮抛光实验的工件表面形貌 |
| In the text | |
 |
图8 不同进给速度vf下砂布页轮抛光表面形貌仿真 |
| In the text | |
 |
图9 抛光表面粗糙度随前倾角θ的变化 |
| In the text | |
 |
图10 不同前倾角θ下抛光工艺砂布页轮抛光实验的工件表面形貌 |
| In the text | |
 |
图11 不同前倾角θ下抛光工艺的砂布页轮抛光表面形貌仿真 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


