| Issue |
JNWPU
Volume 42, Number 1, February 2024
|
|
|---|---|---|
| Page(s) | 70 - 77 | |
| DOI | https://doi.org/10.1051/jnwpu/20244210070 | |
| Published online | 29 March 2024 | |
Region optimization and sensitivity analysis of THT assembly process parameters based on flexible soldering robot platform
柔性焊锡机器人THT组装工艺参数敏感度分析及区间优化
1
Xi’an Electronics Engineering Research Institute, Xi’an 710100, China
2
School of Intelligent Manufacturing and Control Technology, Xi’an Mingde Institute of Technology, Xi’an 710124, China
3
School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China
Received:
6
December
2022
In order to solve the problem that the selection of key process parameters of a flexible soldering robot depends on manual experience, the empirical model of its THT assembly process parameters is established with the response surface method and the reliability of the model is verified. On this basis, the multi-parameter relative sensitivity of the key process parameters is analyzed through the Monte-Carlo simulation, and their single-parameter sensitivity curve is drawn. Then, based on the sensitivity analysis, the stability region division method is designed, and the stability region of process parameters for soldering quality comprehensive score is obtained. The optimal region of process parameters of the soldering robot are acquired by compressing the stability region: soldering temperature from 350-368 ℃, soldering time from 1.31-1.48 s and solder feeding volume from 1.5-2.0 mm3. The average value of the soldering quality comprehensive score within the optimal region of process parameters is 90.2 points.
摘要
针对机器人焊接关键工艺参数的选取依赖人工经验的问题, 通过响应面法建立了自动化焊锡机器人THT组装工艺参数经验模型, 并验证了该模型的可靠性。在此基础上, 利用蒙特卡罗模拟分析关键焊接工艺参数的多参数相对敏感度, 并绘制了单工艺参数区间敏感度曲线。基于敏感度原理设计了工艺参数稳定域划分方法, 获得了面向焊接质量综合分的工艺参数稳定域, 并将该稳定域进行压缩得到机器人焊接工艺参数优选区间为: 加热温度350~368 ℃, 焊接时间1.31~1.48 s, 送锡体积1.5~2.0 mm3, 在工艺参数优选区间内焊接质量综合分平均值为90.2分。
Key words: soldering robot / process parameter / sensitivity analysis / stability region / region optimization
关键字 : 焊锡机器人 / 焊接工艺参数 / 敏感度分析 / 稳定域划分 / 区间优选
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
随着现代相控阵雷达技术向着小型化和轻型化的方向发展, 电子电路模块的集成度和组装密度越来越高, 因此印制板(PCB)组装大多采用表面贴装技术(SMT)。但由于通孔插装元器件的焊点机械强度较高, 对于需要频繁承受机械外力的电子元器件如连接器、长针插座和屏蔽罩等仍然需要采用通孔插装技术(THT)进行组装。近年来, 自动化焊锡机器人以其较高的焊接效率以及对关键焊接工艺参数精确控制等优点[1], 已逐渐取代传统的手工烙铁焊接并广泛应用于THT组装工艺过程中[2]。然而, 在进行机器人焊接时, 焊接关键工艺参数的选取仍然依赖人工经验, 缺乏科学的选择依据, 而不合适的焊接参数容易引起焊点浸润不佳、针孔、吹空、拉尖和假焊等问题, 影响PCB组件的可靠性, 严重时甚至会导致核心电子部件瘫痪。因此, 优化机器人焊接工艺参数、控制THT组装工艺过程是保证雷达核心电子部件质量的关键。
为了提高PCB组件的质量及质量稳定性, 相关学者对PCB组装工艺过程进行了大量研究[3-4]。杨小建等[5]为了解决传统通孔回流焊接工艺中通孔焊点焊锡量不足的问题, 采用预成型焊片进行焊锡量补偿, 并合理设计了混装回流焊接工艺参数。Jing等[6]对回流焊过程中的温度曲线预测模型进行了优化, 提出了一种基于遗传算法的回流温度曲线优化模型并进行了MAPE评价, 结果表明: 该模型可以有效预测温度曲线, 为回流焊生产工艺提供指导。Deeying等[7]采用响应面法研究了激光能量、等待时间、氮气压力和焦点位置对焊点剪切强度和PSA变化的影响, 建立了激光焊接参数与相应期望之间的函数关系, 并通过多目标优化确定了既能提高抗剪强度又能使PSA变化最小的最优工艺参数。针对大铜层或高热容导致的临界焊接情况, Seidel等[8]提出了采用机器学习框架模拟波峰焊工艺过程, 通过使用K-Nearest-Neighbor算法进行建模, 能够准确地预测焊点的孔填充量。Lau等[9]基于灰色田口方法研究了一种优化回流焊接工艺多种性能的创新方法, 使得BGA封装的焊点缺陷率最小化。
从上述学者的研究可以看出, PCB组装工艺过程已受到广泛关注, 焊接工艺参数的优化研究也取得了一定成果[10-11]。然而, 在机器人焊接工艺过程中, 关键工艺参数之间相互耦合, 其相对敏感度及稳定域均无法确定。因此, 本文针对自动化柔性焊锡机器人的THT焊接工艺过程进行分析, 建立工艺参数与焊点质量之间的回归模型。在此基础上, 分析关键焊接工艺参数的多参数相对敏感度及单参数区间敏感度。最后, 基于敏感度原理设计了工艺参数稳定域划分方法, 得到了柔性焊锡机器人THT焊接工艺参数优选区间。
1 柔性焊锡机器人THT组装工艺参数建模
1.1 THT组装工艺过程
柔性焊锡机器人进行通孔插装元器件焊接时的主要工艺流程如图 1所示。
在对某个焊点进行焊接之前需要将烙铁头加热至指定温度并进行预上锡, 其目的是在烙铁头对焊盘和引脚进行预加热时增加接触面积从而保证焊盘和引脚被快速加热。预加热过程完成后便由焊锡丝供给系统以一定的速度进行送锡, 指定量的焊锡丝被送至辅面焊盘后停止送锡, 烙铁头对已送达焊盘的焊锡进行短暂的后加热过程, 使得熔化的焊锡通过通孔流至印制板主面的焊盘, 焊锡与焊盘和引脚形成充分润湿, 随后烙铁头离开焊盘完成该焊点的焊接过程。通过对机器人焊锡工艺过程的分析可以看出, 影响焊接工艺过程的关键工艺参数可归纳为: 烙铁头加热温度、焊接时间和送锡体积。
对于通孔插装元器件的焊接工艺而言, 焊点外观的最佳状态应为焊料充满辅面焊盘、孔壁和主面焊盘且未溢出焊盘, 引脚和焊盘润湿良好且润湿角小于90°, 未出现针孔、拉尖、桥接、不润湿和半润湿等缺陷。目前, 评价焊点焊接质量并无综合的量化指标, 主要依靠焊接操作者目视检查并配合X光透视来评判焊点质量的好坏。因此, 本文采取人工综合评分方式, 让4名有经验的焊接操作者从润湿程度、润湿角、焊点表面形态和焊接缺陷方面对焊点焊接质量进行综合评分(满分为100分), 并取其平均值最终得到焊接质量综合分。
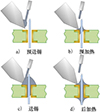 |
图1 机器人焊接工艺过程 |
1.2 实验规划
实验所采用的焊接设备为迈力(北京)机器人科技有限公司研制的七轴柔性焊锡机器人; 焊料为Sn63/Pb37焊锡丝, 直径0.6 mm, 松香含量2.0%;焊接实验的焊点焊盘直径为1.6 mm, 通孔直径为1.0 mm, 通孔长度(印制板厚度)为2.0 mm, 焊点无大面积覆铜; 焊接的插装元器件为连接器, 引脚直径为0.8 mm。
实验以机器人焊接过程中的关键工艺参数如加热温度、焊接时间和送锡体积为自变量, 以焊点焊接质量综合分为因变量, 根据响应面法中的BBD原理进行实验设计。结合手工烙铁焊接经验, 柔性机器人焊接三因素实验设计如表 1所示。
因素及水平表
1.3 实验过程及结果
利用响应面法设计工艺参数组合进行机器人焊接实验, 实验过程如图 2所示。
通过对焊接质量进行综合评分的方式获得每个实验焊点的焊接质量综合分, 便可得到响应面实验结果, 如表 2所示。
根据机器人焊接实验结果, 对实验数据进行回归分析, 建立焊接关键工艺参数与焊接质量综合分之间的多项式经验模型, 如公式(1)所示
式中: S为焊接质量综合分; T, V和t分别为加热温度、送锡体积和焊接时间。
为了验证机器人焊接模型及实验数据的可靠性, 需要进行方差分析、残差分析以及实验值与预测值对比等检验[12]。通过方差分析可知, 焊接质量回归模型失拟项p值为0.289, 大于0.05, 说明实验数据中非正常误差较少, 拟合的经验模型可靠。如图 3所示, 焊接实验结果的残差概率分布图中各点基本处于一条直线上, 分布偏离度较小, 且残差运行图中各点无特定分布规律, 说明实验数据服从常态分布, 无异常数据出现。实验数据的实际值与预测值对比图显示, 实际焊接质量综合分与模型预测值基本一致, 验证了焊接质量回归模型的准确性。
 |
图2 机器人焊接实验 |
机器人焊接响应面实验规划及结果
 |
图3 实验数据及回归模型检验 |
2 多工艺参数相对敏感度分析
通过对机器人焊接工艺及实验数据进行分析可知, 加热温度、焊接时间和送锡体积之间相互耦合对焊点质量产生交互影响。为了掌握每个参数对焊点质量的影响程度, 需要分析上述3个参数的相对敏感度。在机器人焊接工艺参数选择时, 对于较敏感的工艺参数, 需要缩小其选择范围从而保证焊点质量的稳定性。
多参数敏感度分析(multi-parameter sensitivity aanlysis, MPSA)是基于蒙特卡罗模拟对所有参数进行N组取值, 并将其代入模型得到相应的目标函数值, 再通过给定的指标对N次运行的目标函数值进行分类并分别计算其累积频率, 从而得到每个参数的敏感度值[13]。
机器人焊接工艺的MPSA分析步骤为:
1) 确定影响焊接质量的关键工艺参数ki (i=1, 2, 3, …, n);
2) 依据手工焊接经验, 预设每个工艺参数的考查区间;
3) 每个参数都按均匀分布规律在考查区间内随机选取N个参数值ki, j (j=1, 2, 3, …, N);
4) 将随机选取的N组工艺参数组合代入回归模型得到相应的焊接质量综合分yj;
5) 将每次得到的焊接质量综合分与均值(R)进行比较, 确定该组工艺参数组合是“可接受”还是“不可接受”。其中, 均值R可由(2)式得到。
式中: yj为采用第j组参数组合计算出的焊接质量综合分。
“可接受”和“不可接受”的数值pa和pu可由(3)~(4)式得到。
式中: pa为“可接受”; pu为“不可接受”。
6) 工艺参数敏感度计算: 针对每个工艺参数, 统计“可接受”与“不可接受”2组参数的累积频率, 并绘制曲线图。累积频率可由(5)~(6)式得出。
式中: Sa(r)为“可接受”的累积频率; Su(r)为“不可接受”的累积频率。
通过绘制累积频率曲线图, 便可得到分离程度的KS(Kolmogorov-Smirnov distance)值[14], 如(7)式所示, 分离程度的K值越大则说明该工艺参数越敏感。
式中,K为分离程度。
基于焊接质量回归模型, 利用MPSA分析计算焊接过程中关键工艺参数的相对敏感度, 其中, 蒙特卡罗模拟中运行次数被设定为3 000。机器人焊接工艺参数的MPSA分析结果如图 4所示。
图 4中2条曲线分别表示“可接受”和“不可接受”时的累积频率曲线, KS值为2条曲线的最大分离程度。通过MPSA分析得到的各工艺参数分离程度KS值分别为: KT=0.503, Kt=0.317, KV=0.176。因此, 在机器人焊接工艺过程中, 焊接质量对各工艺参数变化的敏感程度由高到低依次为: 加热温度、焊接时间和送锡体积。
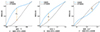 |
图4 MPSA分析结果 |
3 单工艺参数区间敏感度分析
MPSA分析能够得到焊接质量对各工艺参数的相对敏感度值, 但不能获得各工艺参数随取值变化时对焊点质量的影响程度。因此, 需要进行单工艺参数区间敏感度分析(single-parameter sensitivity analysis, SPSA), 从而为单个工艺参数的取值提供依据。
根据区间敏感度的定义[15], 焊接质量对加热温度、焊接时间和送锡体积的区间敏感度模型可由(8)式表示。
式中: T为加热温度范围中值, ℃; t为焊接时间范围中值, s; V为送锡体积范围中值, mm3。
根据焊接质量对单工艺参数的敏感度模型, 分别对加热温度、焊接时间和送锡体积的敏感度进行计算, 其中T=350 ℃, t=1.3 s, V=2.0 mm3。将(1)和(8)式进行联立, 单工艺参数区间敏感度可由(9)式得到。
依据(9)式可以绘制加热温度、焊接时间和送锡体积的敏感度曲线, 如图 5所示。该曲线反映的是每个参数的敏感度变化趋势。采用二分法将每个参数的考察范围进行等分, 可以直观观察到: 加热温度和焊接时间第Ⅰ区间内的敏感度平均值大于第Ⅱ区间, 而送锡体积第Ⅰ区间内的敏感度平均值小于第Ⅱ区间。
 |
图5 单工艺参数敏感度曲线 |
4 机器人焊接工艺参数区间优选
机器人焊接工艺参数稳定域是指焊点质量对工艺参数变化不敏感的取值范围, 而非稳定域是指焊点质量对工艺参数变化较为敏感的参数范围。基于焊接质量二次回归模型, 结合MPSA以及SPSA分析, 可提出基于敏感度的机器人焊接工艺参数稳定域划分方法, 流程如图 6所示。
通过工艺参数稳定域划分方法便可进行焊接工艺参数的稳定域划分。首先, 通过MPSA分析可知, 主要工艺参数如加热温度、焊接时间和送锡体积均为敏感工艺参数, 且已经通过区间敏感度曲线对稳定区间和非稳定区间进行了划分。其次, 利用方法1(见图 6)分别计算稳定和非稳定区间内的焊接质量综合分平均值, 如表 3所示。从中可以看出, 各工艺参数的稳定区间内的焊接质量综合分平均值均大于非稳定区间, 因此, 选择稳定区间作为优选的工艺参数稳定域, 不需要进行二次划分。
其中, 相对敏感度最低的工艺参数为送锡体积, 其相对敏感度K0为0.176, 稳定域范围为1.5~2.0 mm3, 稳定域长度L0为0.5。通过方法2进行压缩, 便可得到加热温度和焊接时间的稳定域长度, 再采用方法3确定压缩后稳定域的位置, 便可得到面向焊接质量的工艺参数稳定域, 在该稳定域内计算出焊接质量综合分平均值为90.2分, 优化结果如表 4所示。
为了验证稳定域内工艺参数的焊接质量, 在稳定域和非稳定域中随机选择3组工艺参数组合进行焊接实验, 并对焊点的综合质量进行评分。所选6组工艺参数以及对应的预测值和实验值如表 5所示。
图 7为6个焊点的X光透视照片。通过对比可以看出, 在稳定域内选择的工艺参数组合所焊接出来的焊点质量综合分平均值为93.4, 明显高于非稳定域内的焊点质量。并且, 稳定域内焊点质量综合分的波动在5分以内。实验结果表明: 优选的焊接工艺参数稳定域具有较好的稳定性和可靠性。
 |
图6 基于敏感度的焊接参数稳定域划分方法流程图 |
优选工艺参数稳定区间划分
焊接工艺参数稳定域
工艺参数稳定域实验验证
 |
图7 工艺参数稳定域实验结果X光透视照片 |
5 结论
本文针对自动化柔性焊锡机器人的THT焊接工艺过程进行分析, 以焊点焊接质量为优化目标, 对机器人焊接工艺过程中关键工艺参数的敏感度及稳定域进行了研究, 研究结果为:
1) 对于焊点的焊接质量而言, 关键工艺参数如加热温度、焊接时间和送锡体积均为敏感工艺参数。通过MPSA分析所得到的各工艺参数相对敏感度KS值分别为: KT=0.503, Kt=0.317, KV=0.176。
2) 通过单工艺参数区间敏感度分析可知, 所有工艺参数的区间敏感度值均呈现出先降后升的规律。
3) 机器人焊接工艺参数稳定域为: 加热温度350~368 ℃, 焊接时间1.31~1.48 s, 送锡体积1.5~2.0 mm3, 在工艺参数稳定域内焊接质量综合分平均值为90.2分。
References
- XIANG L, XING S, LIU Y. Adaptive region control for robotic soldering of flexible PCBs[C]//18th International Conference on Advanced Robotics, Hong Kong, 2017: 216–221 [Google Scholar]
- REN Hao. Robotic micromanipulation for precise assembly and soldering[D]. Beijing: University of Chinese Academy of Sciences, 2021 (in Chinese) [Google Scholar]
- FONSEKA C L S CJAYASINGHE J A K S. Implementation of an automatic optical inspection system for solder quality classification of THT solder joints[J]. IEEE Trans on Components, Packaging and Manufacturing Technology, 2019, 9(2): 353–366 [Article] [CrossRef] [Google Scholar]
- TSIGARAS G, DOLGA V. Robot soldering positions correction with cognex vision camera[C]//New Advances in Mechanisms, Mechanical Transmissions and Robotics, 2021: 444–456 [Google Scholar]
- YANG XiaojianSHEN LiYU Dexue, et al. Study on pin-through-hole reflow soldering process of mixed-mounting printed circuit boards[J]. Aerospace Manufacturing Technology, 2018, 4(2): 44–48 [Article](in Chinese) [Google Scholar]
- JING SLI MLI X, et al. Optimization of reflow soldering temperature curve based on genetic algorithm[J]. Energy Reports, 2021, 7: 772–782 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- DEEYING JASAWARUNGSAENGKUL KCHUTIMA P. Multi-objective optimization on laser solder jet bonding process in head gimbal assembly using the response surface methodology[J]. Optics & Laser Technology, 2018, 98: 158–168 [NASA ADS] [CrossRef] [Google Scholar]
- SEIDEL R, THIELEN N, SCHMIDT K, et al. Development and test of a data framework for prediction of soldering quality in selective wave soldering applying K-nearest neighbors[C]//2020 IEEE 26th International Symposium for Design and Technology in Electronic Packaging, 2020: 250–255 [Google Scholar]
- LAU C SABDULLAH M ZKHOR C Y. Optimization of the reflow soldering process with multiple quality characteristics in ball grid array packaging by using the grey-based Taguchi method[J]. Microelectronics International, 2013, 30(3): 151–168 [Article] [CrossRef] [Google Scholar]
- ABDUL A M SABDULLAH M ZKHOR C Y, et al. Optimization of pin through hole connector in thermal fluid-structure interaction analysis of wave soldering process using response surface methodology[J]. Simulation Modelling Practice and Theory, 2015, 57: 45–57 [Article] [CrossRef] [Google Scholar]
- HAN JGUO FLIU J P. Early stages of localized recrystallization in Pb-free BGA solder joints subjected to thermomechanical stress original research article[J]. Journal of Alloys and Compounds, 2017, 704(15): 574–584 [CrossRef] [Google Scholar]
- ANDERSON M JWHITCOMB P J. RSM simplified: optimizing processes using response surface methods for design of experiments[M]. New York: Productivity Press, 2016 [Google Scholar]
- YU TSHI YHE X, et al. Optimization of parameter ranges for composite tape winding process based on sensitivity analysis[J]. Applied Composite Materials, 2016, 24(4): 821–836 [Google Scholar]
- DENG BSHI YYU T, et al. Multi-response parameter interval sensitivity and optimization for the composite tape winding process[J]. Materials, 2018, 11(2): 220[Article] [NASA ADS] [CrossRef] [Google Scholar]
- KANG CLIU ZSHIRINZADEH B, et al. Parametric optimization for multi-layered filament-wound cylinder based on hybrid method of GA-PSO coupled with local sensitivity analysis[J]. Composite Structures, 2021, 267: 113861 [Article] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图1 机器人焊接工艺过程 |
| In the text | |
 |
图2 机器人焊接实验 |
| In the text | |
 |
图3 实验数据及回归模型检验 |
| In the text | |
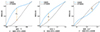 |
图4 MPSA分析结果 |
| In the text | |
 |
图5 单工艺参数敏感度曲线 |
| In the text | |
 |
图6 基于敏感度的焊接参数稳定域划分方法流程图 |
| In the text | |
 |
图7 工艺参数稳定域实验结果X光透视照片 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


