| Issue |
JNWPU
Volume 43, Number 1, February 2025
|
|
|---|---|---|
| Page(s) | 40 - 48 | |
| DOI | https://doi.org/10.1051/jnwpu/20254310040 | |
| Published online | 18 April 2025 | |
Study on head configurations increasing aerodynamic rolling stability of ground-based hypersonic testing system
高超声速地面试验系统头部气动滚转增稳构型研究
1
Norinco Group Testing and Research Institute, Xi'an 710086, China
2
School of Aerospace Engineering, Xi'an Jiaotong University, Xi'an 710049, China
Received:
25
December
2023
Rocket sled testing is a typical high speed, high dynamic and high credibility ground-based high-speed testing technique, which has the ability to simulate the actual operating conditions. The monorail rocket sled is a better choice of the ground-based hypersonic testing system, as its light-weighted and low drag force characteristics. However, the rolling of the rocket sled caused by the impact load is unavoidable in high-speed situation, and the unstable rolling of the rocket sled would cause the severe damage. To prevent the unstable rolling of the monorail rocket sled, this study firstly studied the flow mechanism causing the static rolling stability of a quasi-hypersonic rocket sled using computational fluid dynamics which is that two unsymmetrical quasi-convergent flow channels were formed and cause the velocity and pressure difference on the two sides of the rocket sled. The restoring rolling moment will be introduced by the pressure difference, which is proportional to the rolling angle causing the static rolling stability. Secondly, two designing concepts were promoted from this flow mechanism to increase the static rolling stability including expanding the operating area of the quasi-convergent flow pipe as well as designing secondary quasi-convergent flow pipe. Finally, two configurations named stability-enhancing rudder and quasi-wing were designed in this paper referring to the above designing concepts. 40% rolling stability incensement was reached by stability-enhancing rudder, while 91% was achieved by quasi-wing.
摘要
火箭橇试验是一种可模拟实际工况地面高速、高动态、高可信度的试验技术, 单轨火箭橇系统具有质量轻、阻力小的特点, 是发展高超声速地面试验系统的优选橇型。但其沿单根滑轨高速滑行时受到冲击而产生滚转的现象不可避免, 若发生滚转失稳将导致火箭橇系统出现严重失效。为防止单轨火箭橇系统发生滚转失稳, 采用计算流体力学方法以类高超声速单轨火箭橇模型为研究对象, 对其两侧空间流场进行研究, 探究影响单轨火箭橇系统滚转静稳定性的流动机理, 发现火箭橇系统发生滚转时, 其头部锥形结构会在两侧形成非对称类收缩流道, 直接影响火箭橇头部两侧流速及静压分布, 产生滚转恢复气动力矩, 且随着滚转角增大, 滚转恢复力矩呈增大趋势, 最终形成单轨火箭橇滚转静稳定性。从滚转增稳流动机理出发, 提出2种局部气动增稳外形设计思想, 包括: ①扩大非对称类收缩流道作用面积实现气动增稳; ②设计二次类收缩流道实现气动增稳。对应这2种外形设计思想分别设计出增稳舵构型和头部类翼构型, 两构型均实现了滚转增稳效果, 其中前者增稳40%, 而后者增稳91%。
Key words: hypersonic flow / rocket sled / static rolling stability / computational fluid dynamics
关键字 : 高超声速流动 / 火箭橇 / 滚转静稳定性 / 计算流体力学
© 2025 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
火箭橇[1–2]是一类以火箭发动机为动力, 承载被试品沿着地面高精度滑轨高速运行的地面高精度试验系统, 可以用于模拟飞机、导弹等飞行器的宽速域、高过载飞行工况。与风洞试验和飞行试验相比, 火箭橇试验系统对被试品尺寸及质量的限制大幅降低[3–7],可模拟真实地效环境[8],能够开展被试品动态事件(如侵彻、抛放等)的功能性考核等试验, 同时能够有效获取试验过程中的动态气动、振动测试数据, 可服务于航空航天、兵器、船舶、电子技术、核工业等多行业科研试验。
从20世纪40年代起, 英国、法国、日本、美国等国家都根据自身技术发展需求研制了相应的火箭橇试验系统[2, 9–13], 其中美国火箭橇试验能力发展迅速、设计实力强。至今, 美国已建成了数十个功能各异的火箭橇试验系统[2], 其试验运行速度逐步覆盖了亚/跨/超及高超声速范围, 美国火箭橇试验在2003年最高速度达到8.5Ma[12]。而据公开文献资料显示[3], 我国从1984年建成第1条3 km火箭橇滑轨开始, 历经40余年的高速发展, 目前已建成了长度大于9 km的“亚洲第1轨”, 为吨级载荷、超声速地面试验提供了基础条件。
火箭橇根据其所使用的滑轨数量可分为双轨火箭橇和单轨火箭橇[1]。单轨火箭橇是一类沿着单根轨道高速运行的火箭橇试验系统, 具有体积小、质量轻、气动阻力低的特点[14], 是发展高超声速火箭橇试验能力的首选橇。在运行过程中, 火箭橇系统将受到时变发动机推力[14]、地效作用下的时变气动力[15–16]、轨道不平顺引起的靴-轨冲击载荷[17]及时变靴-轨切应力[14], 以上种种因素均造成了火箭橇系统面临恶劣的振动环境。当火箭橇运行速度达到高超声速阶段后, 轻微的外界扰动即可导致严重的结构动响应[14], 影响其运行稳定性。而单轨火箭橇由于只受到1条滑轨的约束, 其运行稳定性从本质上要远远弱于双轨火箭橇, 因此在设计阶段需要着重考虑其运行稳定性。
为提升单轨火箭橇运行稳定性, 国内外学者[18–21]采用数值模拟方法对火箭橇振动特性进行了分析, 并提出了相应的减震措施, 同时也指出气动设计是保证单轨火箭橇运动稳定性的重要方法之一。近年来, 国内外学者开展了针对单轨火箭橇运行稳定性方面的研究工作。西安交通大学党天娇等[22]发现了滑靴导流板可提供负升力, 从而克服火箭橇自身气动升力导致的运行不稳定, 并利用FFD(free form deformation)方法对滑靴导流板进行了局部优化设计[23]。Yu等[15]利用数值模拟方法研究了乘波体构型火箭橇激波-地面干扰下的气动力频率特征。余元元等[16]采用SAS(scale-adaptive simulation)方法研究了不同马赫数下超声速火箭橇气动力致振机理。邹伟红[24]采用数值模拟方法和工程估算方法开展火箭橇气动阻力和气动特性计算对比研究。房明等[25]研究了尾流对于气动力频率特性的影响。王文杰等[26]采用高精度湍流数值理论与复杂波系干涉理论研究了火箭橇气动激振特性。
以上研究重点在于火箭橇的气动力频率特性研究, 尚未对高超声速单轨火箭橇滚转静稳定性展开系统性深入探索。由于单轨火箭橇运行仅受到1根轨条约束, 相比于其余转动方向, 其在滚转方向上更容易受到外界扰动影响, 整个系统的滚转稳定性较弱,给整个火箭橇试验的实施带来了严重的安全隐患, 在一定程度上决定了试验的成败。因此在实际工程问题中, 单轨火箭橇的滚转稳定性至关重要。
局部气动设计是增强单轨火箭橇滚转稳定性的重要方法之一。本文采用计算流体力学方法, 以类高超声速单轨火箭橇外形为研究对象, 首先分析其自身滚转静稳定性, 从流场入手分析得到单轨火箭橇气动滚转增稳机理。之后为了充分利用该气动滚转增稳机理, 从两方面改进火箭橇局部气动外形, 包括增稳舵构型及机头类翼构型, 并定量地探讨其增稳效果。最后, 总结单轨火箭橇气动滚转增稳外形特征规律, 为高超声速单轨火箭橇气动外形设计提供理论支撑。
1 计算方法
1.1 RANS方程
本文采用ANSYS CFX软件进行流场数值模拟, 软件采用有限体积方法求解可压缩雷诺平均Navier-Stokes方程, 采用全湍流模拟方法, 湍流模型选择两方程SST模型, 离散格式采用高阶迎风格式[27–28], 可压缩RANS方程如(1)式所示。
式中: ρ为空气密度;ui是速度分量;p为压强;E为总能;H为总焓。
1.2 边界条件
1) 进出口边界条件: 流场入口设为速度入口边界条件, 在速度入口处给定速度、相对压力与温度, 流场出口设为压力出口边界条件, 在压力出口处给定相对压力;
2) 物面边界条件: 计算模型表面与远场处设为物面边界条件, 模型表面设为无滑移绝热物面(no slip wall)边界, 远场处设为自由滑移(free slip wall)边界。地面轨道设为滑移绝热物面边界条件, 滑移速度与来流速度保持一致。
1.3 计算状态
1) 大气状态: 大气压强为101 325 Pa, 温度为15 ℃;
2) 来流速度: 6Ma。
1.4 算例验证
为验证本文计算方法对于超声速单轨火箭橇气动特性模拟结果的可靠性, 此处以某3.0Ma单轨火箭橇为对象, 对比橇体头部2个测点不同时刻下CFD计算所得表面静压及试验实测值。图 1及图 2给出了试验对应的火箭橇头部三维几何模型及2处相应的静压测点位置分布。
 |
图1 某3Ma单轨火箭橇试验头部几何模型 |
 |
图2 某3Ma单轨火箭橇试验头部静压测点分布 |
本算例CFD计算采用半模计算, 图 3给出了头部局部表面网格及空间网格分布, 总网格单元数量为470万, 最终静压对比结果如图 4所示。
 |
图3 某3Ma单轨火箭橇头部计算网格分布 |
 |
图4 静压对比曲线 |
从以上静压对比曲线结果可以见, 2个测点处静压实测数据与数值模拟结果具有较好的一致性, 静压预测的最大误差不超过6.25%。
2 计算模型
如文献[11]所述, 高超声速火箭橇结构多以圆锥和圆柱组合作为被试品, 被试品下方存在滑靴以及滑靴整流, 后部安装火箭发动机。此处仿照文献[12]中美国8.5Ma火箭橇试验纹影照片(如图 5所示), 建立类高超声速单轨火箭橇模型, 并以此为对象开展本文研究。
图 6给出了上述类高超声速单轨火箭橇模型, 该模型由机头、推力橇组成。其中机头包含了被试品及机头滑靴, 而推力橇则包含了发动机、滑靴及两者之间的连接橇体, 本文后续将此模型称为标准构型。
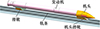 |
图6 类高超声速单轨火箭橇模型 |
本文拟对标准计算模型进行2种局部气动改型设计, 并研究其增稳特性。
1) 增稳舵构型: 借鉴飞行器设计中翼尖小翼设计[29], 在火箭橇机头位置设计增稳舵面, 使其提供额外的气动滚转恢复力矩, 如图 7所示。
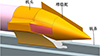 |
图7 增稳舵构型 |
2) 机头类翼构型: 结合机头处整流面, 将整流头锥内收, 在头锥帽下沿设计出类翼结构的下侧面, 从而利用特定的翼面角度提供额外的气动滚转恢复力矩, 如图 8所示。
 |
图8 机头类翼构型 |
3 计算网格
本文数值计算所用流场域为1/2圆柱体, 具体包含火箭橇几何外形、滑轨、水泥承轨梁、地面以及远场边界, 如图 9所示。其中远场半径为火箭橇模型包络半径的70倍, 而流场域流向长度则为火箭橇模型长度的13倍。
 |
图9 流场域模型 |
如图 10所示, 本文采用ANSYS ICEM生成非结构四面体网格, 在物面附近生成边界层, 物面法向首层网格高度为0.001 mm, 法向增长率为1.1, 边界层法向网格层数为30层。同时为了更加详尽地捕捉计算模型附近、机头与地面轨道系统之间的流动特征, 在机头附近及靴-轨之间流动区域内进行局部网格加密, 最终所得网格单元总数为1 120万。
 |
图10 非结构计算网格 |
4 计算结果与讨论
4.1 标准构型及增稳舵构型
本小节主要对比在不同滚转角度状态, 原始标准构型及增稳舵构型可以提供的气动滚转恢复力矩。两构型计算所得滚转恢复力矩曲线如图 11所示。
 |
图11 标准构型和增稳舵构型滚转恢复力矩 |
其中滚转角大于0°表示火箭橇系统发生右滚, 而滚转恢复力矩为正表示系统受到左滚气动力矩。若滚转恢复力矩的斜率为正, 表示当火箭橇系统发生右滚时, 其所受到的气动滚转恢复力矩增量为左滚力矩, 即该火箭橇系统存在静稳定性, 反之则该系统不存在静稳定性。
进一步, 系统滚转恢复力矩曲线斜率的绝对值大小则直接反映其静稳定能力的强弱, 绝对值越大表示系统静稳定能力越强。
根据该计算结果可知, 标准构型和增稳舵构型均存在滚转静稳定性。通过最小二乘拟合可得, 标准构型滚转恢复力矩曲线斜率为45 N·m/(°), 而增稳舵构型所对应的曲线斜率为63 N·m/(°), 因此增稳舵构型的滚转静稳定性要强于标准构型。
在大滚转角状态下, 增稳舵构型所对应滚转恢复力矩曲线斜率明显增大, 由63 N·m/(°)增大至70 N·m/(°), 这一现象说明增稳舵在大滚转角状态下的增稳效果有所增强。
标准构型机头锥面形状是造成其存在滚转静稳定性的根本原因之一, 当火箭橇系统发生滚转时, 其头部存在接近地面一侧和远离地面一侧, 如图 12所示。
 |
图12 火箭橇滚转示意 |
在上述远离地面和接近地面的一侧, 其头部锥面形状和地面之间均形成了类收缩流道, 但在接近地面一侧流道收缩比要高于远离地面一侧, 从而导致相同位置处, 接近地面一侧的流速低于远离地面一侧, 而接近地面一侧静压要高于远离地面一侧。且随着火箭橇系统滚转角的增大, 机头两侧流道收缩比差异也将增大, 上述流速、静压差异也将更加凸显。
为了更清晰地说明头部两侧非对称的类收缩流道对于单轨火箭橇滚转静稳定性的作用, 这里截取2组不同滚转角状态下的法向流场平面如图 13所示。
 |
图13 标准构型头部法向截面位置 |
图 14为标准构型6°滚转角状态, 头部法向截面马赫分布云图, 图中A、B两点为流向位置相同且侧向位置对称的两点, 其中A点位于接近地面一侧收缩流道内, B点位于远离地面一侧收缩流道内, 从图中可知, A点处流速低于B点。而图 15为标准构型6°滚转角状态下, 头部法向截面静压分布云图, 从图中可清晰地判断出接近地面一侧静压高于远离地面一侧。图 16~17分别给出了标准构型3°滚转角状态下, 头部两侧流场法向平面的速度、静压分布云图。当火箭橇滚转角为3°时, 其头部两侧类收缩流道的收缩比差异要弱于滚转角为6°的状态, 致使A、B两点的流速、静压差异减弱。与图 11所示结果一致, 滚转角3°时橇体所产生的滚转恢复力矩要小于滚转角为6°时的情况。
 |
图14 标准构型6°滚转角头部法向截面静压分布 |
 |
图15 标准构型6°滚转角头部法向截面马赫分布 |
 |
图16 标准构型3°滚转角头部法向截面马赫分布 |
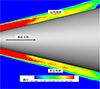 |
图17 标准构型3°滚转角头部法向截面静压分布 |
火箭橇滚转状态下机头两侧空气静压差作用于机头侧面, 主要产生垂直于对称面的气动力, 从而产生火箭橇滚转恢复力矩。在相同压力差的情况下, 该滚转恢复力矩的大小与机头几何外形在对称面内的投影面积呈正相关关系。在机头上方布置增稳舵则有利于增加该投影面积, 从而实现火箭橇系统的气动滚转增稳。
另外, 在机头上方加入增稳舵之后, 产生了类似飞机翼尖小翼的效果, 增稳舵对机头两侧流动形成阻隔作用, 从而维持了两侧压差, 进一步起到增稳作用。为了清楚说明增稳舵的作用, 这里截取如图 18所示流向2个不同位置处的流场平面。
 |
图18 增稳舵构型头部流向截面位置 |
图 19~20分别为头部流向截面1位置处标准构型和增稳舵构型的静压分布云图。图 21~22为头部流向截面2位置处标准构型和增稳舵构型的静压分布云图。从这4幅静压分布云图看, 增稳舵构型可以在机头顶部维持火箭橇机头两侧较高的静压差, 同时相比于标准构型上述静压差的作用面积也进一步增大。以上两点最终导致增稳舵构型的滚转静稳定性优于标准构型, 如图 11所示。
 |
图19 标准构型头部流向截面1静压分布 |
 |
图20 增稳舵构型头部流向截面2静压分布 |
 |
图21 标准构型头部流向截面1静压分布 |
 |
图22 增稳舵构型头部流向截面2静压分布 |
4.2 机头类翼构型
通过上述流场分析, 标准构型产生滚转后其锥形机头在机头两侧形成了非对称类收缩流道, 从而产生气动滚转恢复力矩。为了进一步利用这一流动机理, 在机头下方以一定角度布置类翼结构, 这里以机头前端点为轴心, 相对水平面倾角分别为3°和1°倾角为例进行研究, 如图 8所示。
当火箭橇发生滚转时,标准构型头部两侧形成收缩比不同的收缩流道,在纵向对称面法向产生气动力差量,进而产生滚转恢复力距。此处利用头部下方斜切类翼结构,在原有收缩流道的基础上形成二次收缩流道,进一步增大头部两侧压力差,同时在二次流道内部可形成切向气动力差量,提供额外的滚转恢复力矩。
图 23给出了标准构型气动力方向与此处类翼构型中二次流气动力的方向示意。机头下方斜切角度越大, 其形成的二次收缩流道收缩比差别越大, 最终产生的滚转增稳效果也越强。
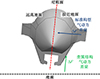 |
图23 标准构型及类翼构型气动力方向示意 |
图 24给出了本小节机头类翼构型对比计算结果, 通过最小二乘拟合可知, 1°倾角构型计算所得滚转恢复力矩曲线斜率为56 N·m/(°), 3°倾角构型所对应曲线斜率为86 N·m/(°)。图 24曲线所示结果与上述分析一致, 机头类翼构型可以产生滚转效果, 同时斜切角度的增大直接增大了滚转恢复力矩曲线斜率, 这意味着火箭橇系统的滚转静稳定性增强。单轨火箭橇滚转静稳定性的强弱仅与其滚转恢复力矩随滚转角变化的曲线斜率有关, 滚转恢复力矩的绝对值则与其具体气动外形相关。类翼斜切结构破坏了原有标准构型机头部分锥面, 这就导致不同构型火箭橇的基准状态并不一致, 其滚转恢复力矩的绝对值出现一定的差异。
 |
图24 标准构型和机头类翼构型滚转恢复力矩 |
5 结论
本文采用计算流体力学方法对类高超声速单轨火箭橇构型的气动滚转静稳定性展开研究。首先基于流动机理, 分析得到了单轨火箭橇滚转静稳定性的成因, 并由此提出了2种局部滚转增稳气动构型, 之后对比了其滚转增稳效果。具体结论如下:
1) 当单轨火箭橇发生滚转时, 其头部锥面形状将在火箭橇头部两侧形成非对称类收缩流道, 从而在机头两侧形成压力差, 进一步产生滚转恢复力矩。该滚转恢复力矩的大小与流道作用面积和两侧流道收缩比的差量正相关。
2) 通过在机头顶部设置增稳舵可以实现单轨火箭橇滚转增稳, 一方面增稳舵增加了两侧非对称流道的作用面积, 另一方面增稳舵将两侧非对称流道隔开, 维持了两侧压力差。本文所设计增稳舵实现了40%滚转增稳效果。
3) 通过在机头下方设计类翼结构可以实现单轨火箭橇滚转增稳, 类翼结构通过水平斜切头部锥面, 产生了二次类收缩流道, 造成机头两侧的压力差进一步增大, 在橇体对称面法向及切向均产生气动力差量。本文所设计两种机头类翼构型分别实现了24%及91%的滚转增稳效果。
References
- TIAN JianmingJING JianbinHAN Guangqi. Overview on hypersonic aircraft ground test method[J]. Journal of Detection & Control, 2013, 35(5): 57–60 (in Chinese) [Google Scholar]
- WALIA ShilpaSATYA VikrantMALIK Sandeep, et al. Rocket sled based high speed rail track test facilities: a review[J]. Defence Science Journal, 2022, 72(2): 182–194 [Article] [Google Scholar]
- ZHOU XuewenYAN HuadongCHEN Cheng, et al. Review on rocket sled test methods[J]. Journal of Ordnance Equipment Engineering, 2023, 44(suppl.1): 398–404 (in Chinese) [Google Scholar]
- XIA QiangWU XiaosongSUN Bo, et al. Numerical simulation and experimental investigation on mixed-compression inlet of solid fuel ramjet extended-range projectile[J]. Acta Armamentarii, 2010, 31(10): 1372–1378 (in Chinese) [Google Scholar]
- XUE DongLIU JinWANG Huan, et al. Design of dynamic derivative test system for projectile/rocket model in high-speed wind tunnel[J]. Acta Armamentarii, 2021, 42(11): 2522–2530 (in Chinese) [Google Scholar]
- LI XiaohuiWANG HongweiXIONG Hongliang, et al. Experimental study on the flow characteristics in the leeward region over a slender body of revolution under high-speed condition[J]. Acta Armamentarii, 2024, 45(3): 818–827 (in Chinese) [Google Scholar]
- GOTO KeisukeKATO YuichiISHIHARA Kazuki, et al. Thrust validation of rotating detonation engine system by moving rocket sled test[J]. Journal of Propulsion and Power, 2021, 373): 419–425 [Google Scholar]
- DOIG G. Transonic and supersonic ground effect aerodynamics[J]. Progress in Aerospace Sciences, 2014, 69: 1–28 [Google Scholar]
- NAKATA DaisukeNISHINE KenjiTATEOKE Kaoru, et al. Aerodynamic measurement on the high speed test track[J]. Transactions of the Japan Society for Aeronautical and Space Sciences, 2014, 12(29): 5–10 [Google Scholar]
- GUROL Husam, KETCHEN Don, HOLLAND Leo, et al. Status of the holloman high speed maglev test track(HHSMTT)[C]//30th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, 2014: 2655 [Google Scholar]
- HOOSER Michael, SCHWING Anna. Validation of dynamic simulation techniques at the holloman high speed test track[C]//38th Aerospace Sciences Meeting and Exhibit, 2000: 155 [Google Scholar]
- MINTO David. CTEIP funded advances in hypersonic testing at the Hollman high speed test track[C]//24th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, 2004: 2740 [Google Scholar]
- LOFTHOUSE Andrew, HUGHSON Montgomery, PALAZOTTO Anthony. Computational aerodynamic analysis of the flow field about a hypervelocity test sled[C]//41st Aerospace Sciences Meeting and Exhibit, 2003: 981 [Google Scholar]
- DANG TianjiaoLIU ZhenZHOU Xuewen, et al. Dynamic response of a hypersonic rocket sled considering friction and wear[J]. Journal of Spacecraft and Rockets, 2022, 59(4): 1289–1303 [Google Scholar]
- YU YuanuuanWANG BinXU Changyue, et al. Aerodynamic characteristics of supersonic rocket-sled involving waverider geometry[J]. Applied Sciences, 2022, 12(15): 7861 [CrossRef] [Google Scholar]
- YU YuanyuanWANG FangyuanWANG Bin, et al. Analysis on flow characteristics and aerodynamic-force-induced vibration of supersonic rocket-sled[J]. Journal of Northwestern Polytechnical University, 2022, 40(5): 1080–1089 [Article] (in Chinese) [Google Scholar]
- HOOSER Michael. Simulation of a 10 000 f/s ground vehicle[C]//21st Aerodynamic Measurement Technology and Ground Testing Conference, 2000: 2290 [Google Scholar]
- SUN YiZHANG QiZHAO Liangyu. Study on modal and vibration characteristics of the dual track rocket sled system[J]. Journal of Ordnance Equipment Engineering, 2023, 44(5): 165–171 (in Chinese) [Google Scholar]
- ZHAO XiangweiYANG ZhenYANG Yang. Numerical analysis for slipper-rail contact characteristics of rocket sled[J]. Journal of Vibration and Shock, 2022, 41(1): 238–243 (in Chinese) [Google Scholar]
- FAN KunYANG ZhenXUE Xiaomin, et al. Transmission characteristics of impact response of monorail rocket sled[J]. Chinese Journal of Applied Mechanics, 2020, 37(5): 1887–1893 (in Chinese) [Google Scholar]
- FU LiangDONG LongleiZHAO Xiangwei, et al. Evaluation and test research on damping effectiveness of damping slippers[J]. Journal of Ordnance Equipment Engineering, 2023, 44(7): 116–120 (in Chinese) [Google Scholar]
- DANG TianjiaoLIU ZhenZHOU Xuewen, et al. Numerical investigation on aerodynamic parameters of deflector of hypersonic rocket sled[J]. Journal of Solid Rocket Technology, 2020, 43(3): 355–363 (in Chinese) [Google Scholar]
- DANG TianjiaoLI BingfenHU Dike, et al. Aerodynamic design optimization of a hypersonic rocket sled deflector using the free-form deformation technique[J]. Journal of Aerospace Engineering, 2021, 235(15): 2240–2248 [Google Scholar]
- ZOU Weihong. Computational aerodynamic simulation of the rocket sled[D]. Nanjing: Nanjing University of Science & Technology, 2008 (in Chinese) [Google Scholar]
- FANG MingSUN JianhongWANG Conglei, et al. Analysis of wake flow characteristics for low subsonic rocket sled[J]. Acta Aerodynamica Sinica, 2017, 35(6): 897–901 (in Chinese) [Google Scholar]
- WANG WenjieZHAO XuYANG Long, et al. Study on aerodynamic mechanism of strong ground effect on horizontal boost run cross velocity domain[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(21): 528247 (in Chinese) [Google Scholar]
- ZHANG ChuanxiaLYU ShuiyanXIE Botao, et al. Study on aerodynamic characteristics of the wing of winged rocket sled under strong ground effect environment[J]. Journal of Ordnance Equipment Engineering, 2018, 39(9): 89–92 (in Chinese) [Google Scholar]
- PAN JinshanSHAN Peng. Fundamentals of gasdynamics[M]. Beijing: National Defense Industry Press, 2012 (in Chinese) [Google Scholar]
- WANG HuiCHEN Zezhou. Numerical simulation analysis of different winglets under medium-high speed conditions[J]. Journal of Civil Aviation University of China, 2021, 39(4): 8–12 (in Chinese) [Google Scholar]
All Figures
 |
图1 某3Ma单轨火箭橇试验头部几何模型 |
| In the text | |
 |
图2 某3Ma单轨火箭橇试验头部静压测点分布 |
| In the text | |
 |
图3 某3Ma单轨火箭橇头部计算网格分布 |
| In the text | |
 |
图4 静压对比曲线 |
| In the text | |
 |
图5 Holloman基地火箭橇试验[12] |
| In the text | |
 |
图6 类高超声速单轨火箭橇模型 |
| In the text | |
 |
图7 增稳舵构型 |
| In the text | |
 |
图8 机头类翼构型 |
| In the text | |
 |
图9 流场域模型 |
| In the text | |
 |
图10 非结构计算网格 |
| In the text | |
 |
图11 标准构型和增稳舵构型滚转恢复力矩 |
| In the text | |
 |
图12 火箭橇滚转示意 |
| In the text | |
 |
图13 标准构型头部法向截面位置 |
| In the text | |
 |
图14 标准构型6°滚转角头部法向截面静压分布 |
| In the text | |
 |
图15 标准构型6°滚转角头部法向截面马赫分布 |
| In the text | |
 |
图16 标准构型3°滚转角头部法向截面马赫分布 |
| In the text | |
 |
图17 标准构型3°滚转角头部法向截面静压分布 |
| In the text | |
 |
图18 增稳舵构型头部流向截面位置 |
| In the text | |
 |
图19 标准构型头部流向截面1静压分布 |
| In the text | |
 |
图20 增稳舵构型头部流向截面2静压分布 |
| In the text | |
 |
图21 标准构型头部流向截面1静压分布 |
| In the text | |
 |
图22 增稳舵构型头部流向截面2静压分布 |
| In the text | |
 |
图23 标准构型及类翼构型气动力方向示意 |
| In the text | |
 |
图24 标准构型和机头类翼构型滚转恢复力矩 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


