| Issue |
JNWPU
Volume 43, Number 1, February 2025
|
|
|---|---|---|
| Page(s) | 49 - 57 | |
| DOI | https://doi.org/10.1051/jnwpu/20254310049 | |
| Published online | 18 April 2025 | |
Influence of ventilation parameters on water entry cavitation of disk cavitation vehicle
通气参数对圆盘空化器航行体入水空泡的影响
1
School of Marine Science and Technology, Northwestern Polytechnical University, Xi'an 710072, China
2
Military Representative Bureau of the Army Equipment Department in Xi'an, Xi'an 710032, China
Received:
13
October
2023
In order to explore the impact of ventilation parameters on the characteristics of water entry cavitation, the VOF multi-phase flow model, the realizable k-ε turbulence model and the Singhal cavitation model are used to establish the high-speed water entry flow field simulation method. The comparison with the experimental results from open literature verifies the feasibility of the simulation method. The influence of ventilation parameters on the ventilation super-foam shape is studied. The results show that the ventilation from behind a cavitation device is conducive to the generation and development of a water entry super-foam and can promote the gas flow in the foam, extending the time for water entry foam closure and increasing its size. When the cavitation is not closed at the beginning of water entry, ventilation or not has little effect on the shape of the foam, whose maximum diameter difference is within 0.015D. In the continuous water entry process, the size of the foam increases with the increasing ventilation, which increases the foam size significantly. When the ventilation rate is 4.74, the length of the foam increases by 0.32D; its diameter increases by 25%. The ventilation from behind the cavitation device can delay water entry foam closure. The greater the amount of ventilation, the longer the time for foam closure. When the ventilation rate is 2.37, the closure time is 3.2 ms; when the ventilation rate is 4.74, the closure time is 4 ms, indicating that when the amount of ventilation doubles, the foam closure delays by 25%.
摘要
为探究通气参数对入水空泡特性的影响, 采用VOF多相流模型、Realizable k-ε湍流模型和Singhal空化模型, 建立了高速入水流场非定常数值仿真方法, 通过与文献公开的试验结果进行对比, 验证了仿真方法的可行性, 研究了通气参数对通气超空泡形态的影响规律。结果表明: 空化器后通气有利于入水超空泡的生成和发展并会改变泡内气体流动特性。通入空气能够促使泡内气体回旋流动, 使得入水空泡闭合时间得以延迟, 入水空泡尺寸增加。在入水初期空泡还未闭合, 是否通入空气对空泡形态的影响不大, 空泡最大直径差值在0.015D以内; 在持续入水过程中, 空泡尺寸随通气量的增加而增大, 通入空气使得空泡尺寸显著增加, 通气率为4.74时, 空泡长度增加了0.32D, 空泡直径增加了25%。在空化器后方通入空气可使得入水空泡闭合延迟, 通气量越大, 空泡闭合所需时间越长。通气率为2.37, 空泡3.2 ms闭合, 通气率为4.74, 空泡4 ms闭合, 可见通气量增加1倍, 空泡闭合时间在原来的基础上可延迟25%。
Key words: artificial ventilation / cavitation / ventilation / multi-phase flow
关键字 : 人工通气 / 空化 / 通气量 / 多相流
© 2025 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
跨介质航行器能够兼顾空中飞行器航程远、速度快和水下航行器隐蔽性好的优势, 是对抗大型水面舰船的杀手锏。在水下阶段, 采用超空泡技术的跨介质航行器, 突防能力能够得到进一步提高, 受到了广泛关注。该类跨介质航行器一般具有入水速度高、流体动力特性复杂和入水流场非定常特性强等特点, 这给入水空泡演变特性预测和形态控制带来了挑战。
入水问题的研究始于19世纪末, Worthington等[1]对刚性球体的垂直入水过程进行了试验研究。对于入水稳定性问题, Mirzaei等[2]研究了高速航行体的入水弹道稳定性, 考虑了滑行力和空泡特性变化对运动的影响, 建立了能够预测航行体滑行的模型。黄鸿鑫等[3]通过数值仿真研究了高速入水的射弹运动特性, 发现航行器的入水稳定性受空泡形态、空化器外形和质心位置的影响。在入水空化特性方面, Yu等[4]对高速射弹入水空泡的发展过程进行了理论分析, 揭示了自然空化和通气空化情况下航行器的流体动力特性, 获得了入水过程中的空泡形态变化规律。Shi等[5]对高速入水的球体开展了试验研究, 探讨了入水弹道偏转的原因, 得到了球体速度随水深变化的经验公式并预测了水下空泡闭合的理论深度。Truscott等[6–7]开展了射弹入水试验, 发现空泡内部存在大量的水蒸气, 证实了高速工况下的自然空化现象。邹志辉等[8]在喷气入水试验中研究了不同通气量对空泡形态的影响, 发现空泡直径随喷气系数呈线性增加。赵海瑞等[9]采用CFD方法, 发现了通气斜入水工况的弹道偏转现象并指出该现象产生的原因与入水空泡不对称性有关。陈诚、曹伟等[10–11]分别采用试验和数值仿真的方法, 探讨了通气对航行器运动状态的影响, 发现航行器的运动稳定性与入水空泡的形态密切相关, 通气会导致空化数降低, 影响入水空泡, 进而影响航行体的运动稳定性。
当前关于通气超空泡航行器入水的研究主要集中在空泡流型预测、入水弹道等方面, 关于通过人工通气的方法主动控制入水空泡形态的研究鲜见报道。事实上, 跨介质超空泡航行器在入水过程中的通气行为有可能导致入水空泡演变过程发生显著变化, 进而影响入水弹道稳定性。因此, 需要探究人工通气对入水空泡形态及发展过程的影响。
本文针对通气超空泡航行器高速垂直入水过程, 考虑人工通气、多相流、湍流和空化等问题, 建立了航行器高速入水流场非定常数值模型, 研究了通气参数对入水空泡的发展过程及空泡形态特征的影响。研究结果可为跨介质超空泡航行器的总体设计和工程应用提供参考。
1 高速入水流场非定常数值模型
1.1 数值计算方法
1.1.1 多相流模型
跨介质超空泡航行器入水流场涉及空气、水及水蒸气的三相流动, 气液之间具有明确的相间界面。该类问题使用VOF多相流模型进行建模, 能够获得较高精度的计算结果[12]。
考虑到流场中水的温度没有发生明显变化, 在建立数值模型时忽略了能量方程。因此, 高速入水流场的控制方程包括连续性方程和动量场方程。
1) 连续性方程
由于流场中马赫数远小于0.3, 可将流场视为不可压缩流场, 其连续性方程可简化为
式中: ρm为多相流混合密度; vm表示多相流混合平均速度; vk为多相流第k相的速度; αk为多相流第k相的体积分数; ρk为多相流第k相的密度; n为多相流的相数, 对于水下流场n=2, 对于入水流场n=3。
2) 动量守恒方程
在VOF多相流模型中混合项的动量守恒方程可描述为
式中: p表示流场静压; S表示自定义动量源项, 本研究中该项为0;vi和vj表示混合相的速度分量; μ表示混合相动力黏度。
1.1.2 湍流模型
在高速流场通气空泡发展过程中, 超空化的非定常行为与湍流结构的生成与演化特性密切相关, 且涉及相间质量传递问题。本文选用Realizable k-ε湍流模型, 该模型能够更好地预测超空化流场中的空泡演变过程和空泡形态[13]。
模型的基本方程为
式中: ρ为介质密度; μ为绝对黏度; μt=ρCμk2/ε为湍流黏性系数, 其中Cμ是平均应变率与旋度的函数, 在平衡边界层惯性底层Cμ=0.09;Gk为速度梯度引起的湍流动能; Gb为浮力引起的湍流动能; S=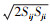 , 其中Sij和Sji分别表示为i方向到j方向和j方向到i方向的平均速度应变率张量; C1=
, 其中Sij和Sji分别表示为i方向到j方向和j方向到i方向的平均速度应变率张量; C1=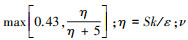 为运动黏度系数; 模型常数σk=1.0, C2=1.9, C1ε=1.44。
为运动黏度系数; 模型常数σk=1.0, C2=1.9, C1ε=1.44。
1.1.3 壁面函数
由于Realizable k-ε模型难以捕捉湍流边界层到过渡层区域的特性, 本文采用尺度化壁面函数对近壁面区域进行处理。
尺度化壁面函数为
y*满足(9)式。
Up为p点的平均流速; kp为p点的湍流动能; τw为壁面切应力; y*表示标准壁面函数在该区域的无量纲距离; yp为p点到壁面的距离; von Kármán常数κ=0.418 7;经验系数E=9.793。
1.1.4 空化模型
流场存在水相与水蒸气相之间的质量传递, 空气作为非凝态气体对空化过程存在一定的影响。Singhal空化模型考虑了相变、空泡流体动力、湍流和非凝相气体等因素的影响, 能够用于描述高速入水过程中水和蒸气的相间质量传递[14]。
Singhal空化模型中水和水蒸气之间的质量传递速率可描述为
式中: 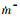 为蒸发率;
为蒸发率; 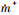 为凝结率;
为凝结率; 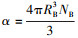 为气相体积分数, 其中NB为单位体积内包含的球形气泡数量, RB为气泡半径; pc为水的饱和蒸气压; p∞为环境压力; ρg, ρl分别为气相密度和液相密度; 模型常数rnuc=5×10-5, Fv=50, Fc=0.01。
为气相体积分数, 其中NB为单位体积内包含的球形气泡数量, RB为气泡半径; pc为水的饱和蒸气压; p∞为环境压力; ρg, ρl分别为气相密度和液相密度; 模型常数rnuc=5×10-5, Fv=50, Fc=0.01。
1.2 计算域及边界条件
由于航行器的后体完全被包裹于超空泡中, 对于入水空泡的演变过程影响有限。为了进一步减小计算量, 突出核心流场的流动特征, 所以将航行器简化为由空化器、通气段和柱段组成的平头圆柱体。
以航行器为参考系, 来流与航行器之间存在相对运动, 将计算域右侧设为速度入口, 左侧设为压力出口, 通气孔采用速度入口条件, 通过改变通入气体流速控制气体的体积流量变化, 通气介质为300 K的空气。通气率Cq表示通气体积流量大小, 可描述为
式中: Q为通气体积流量; u为来流速度; dn为空化器直径。
由于流域壁面对航行体入水的流场边界存在剪切作用, 若流域较小将会拉伸空泡的长度并压缩空泡的直径。许海雨等[15]指出, 高弗劳德数通气超空泡的流域径向尺寸至少为理论最大空泡直径的54倍时, 可忽略流域边界剪切作用的影响。弗劳德数Fr表征惯性力和重力的关系, 具体表达式为
式中: u为来流速度; g为重力加速度; dn为空化器直径。此模拟的来流速度为50 m/s, 弗劳德数Fr=225.76, 确定流域径向尺寸为108D。
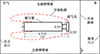 |
图1 计算域及边界条件 |
1.3 网格划分
由于通气超空化的生成和发展过程中存在剧烈的湍流运动和气液两相能量交换, 为了提高计算精度得到更为准确的通气空化特性, 本文预估了空泡生成区域并对模型壁面周围的网格进行了局部加密, 将60%以上的网格集中于通气超空化区域, 最终网格数量约70万。
 |
图2 航行器附近的网格划分情况 |
1.4 网格无关性验证
为排除网格数量对计算精度的影响, 保持计算域大小、分块方法和边线节点分布规律不变, 仅改变节点数量, 对网格数量为30万,70万,105万的模型进行验证计算。以航行体50 m/s入水、通气系数为0.79的工况为例。观察并分析曲线可知, 105万网格和70万网格, 空泡闭合尾部基本重合。为节省计算资源, 选择网格量为70万的计算域即可满足计算精度要求。
 |
图3 不同网格量的空泡轮廓对比图 |
1.5 数值方法验证
郭子涛[16]基于高速摄影技术, 对平头细长圆柱体高速入水问题开展了系列试验研究, 获得了入水空泡、航行速度随时间的演变过程。采用前述的数值仿真方法, 对文献[16]中以初速度603 m/s入水的∅12.65 mm×25.4 mm圆柱体进行仿真验证。提取观测点处空泡轮廓线与文献[16]中的数据, 将入水时间为0.222, 0.444, 0.666 ms时空泡的数值仿真结果与文献[16]试验结果对比, 如图 4所示。可以看出, 观测点与数值仿真所得轮廓线基本重合, 空泡截面直径相对偏差为2.78%。说明本文所采用的数值仿真方法适用于研究平头细长体入水过程中的空泡演变过程和空化特性。
 |
图4 试验与数值仿真结果对比 |
2 数值仿真与结果分析
超空泡航行器入水的流体动力特性与空泡和航行器的位置关系有关, 通气量的差异导致超空泡形态发生显著变化。为探究通气量对空泡形变的控制规律, 以50 m/s入水的航行体为对象, 对比研究系列通气条件下的空泡差异。
图 5为不同通气率下航行体在50 m/s入水过程中不同时刻的入水空泡形态演变图, 红色为水相, 蓝色为气相。由图可知, 通气的空泡形态与不通气时基本相同, 但空泡的发展趋势有较大差别。对比发现,通气有利于入水超空泡的生成和发展并会改变泡内气体流动特性, 对超空泡流型的发展有影响。
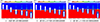 |
图5 不同通气率的入水空泡形态演变图 |
为了探究通气量与空泡流型的关系, 进一步分析图 6, 图中左半部分为压强云图, 右半部分为密度云图与泡内气体矢量叠加图。其中密度云图的蓝色部分为水相, 红色部分为气相, 彩色过渡区密度约为500 kg/m3,可视作空泡轮廓。
 |
图6 泡内气体速度矢量与压强叠加图 |
从图 6a)~6b)的空泡轮廓可以看出相同入水时间内的空泡发展趋势不同, 此时未通气的空泡已经有闭合的趋势而通气的情况下仍为开口空泡。观察空泡尾部位置发现, 未通气时空泡尾部与航行体表面存在高压区, 使得自由液面处空气受高压梯度的影响发生分流, 绝大部分向下游流动重新汇入大气中; 小部分气体反向流入空泡内, 形成空泡内部的漩涡区, 这部分气体经过回旋能够沿空泡边界流动, 其流动方向与空泡边界平行, 因此外部高压区使得空泡向航行体表面发展进而使空泡闭合。通气工况下尾部低压区存在气体小漩涡, 漩涡边界的气体经过回旋后, 携带部分涌入的空气沿航行体表面向头部流动, 直到与通气孔处的气体汇合再反向沿空泡边界流动, 导致空泡的径向尺寸较大; 还有小部分漩涡中心附近的气体直接垂直流向空泡尾部, 促使空泡持续敞开。
由图 6c)~6d)可知, 通气孔处的压强相差不大, 通入的气体在肩部形成气体漩涡后沿着航行体向下游流动, 通气量的增加促使泡内气体流动在肩部以下位置回旋产生气体小漩涡, 使得气体持续流动并拉长空泡, 空泡闭合后绝大部分气体堆积于空泡尾部, 空泡最大直径位于尾部。
3 通气量对空泡特性的影响分析
3.1 通气量对入水空泡形态的影响
为了研究通气量对超空泡生成和演变过程的影响, 本文在宽范围通气量内, 对系列通气量开展了空泡生成及演化特性的研究。图 7为弹体在不同通气条件下入水过程中的空泡特性曲线, 其中弹体入水速度为50 m/s, 通气率分别为0, 0.79, 1.58以及2.37。下面结合图 7进行深入分析。
 |
图7 系列通气率仿真结果对比 |
从0.45 ms和0.95 ms的空泡特性曲线可看出, 在弹体撞水的瞬间, 自由液面受到强烈的冲击作用, 在极短的时间内存在较大的能量交换, 弹体的动能传递给四周的水, 水被径向排开并沿着弹体表面向上喷溅至自由液面。由于在撞水时弹体的惯性远大于其重力, 故这一阶段空泡初生并不断扩大。在不同的通气量条件下, 撞水开口空泡阶段的空泡轮廓线几乎重合, 因此,通气导致开口空泡最大直径的变化量不超过0.015D。
弹体逐渐入水, 空泡的轴向尺寸逐渐拉长, 空泡直径也逐渐增大, 由于空泡敞开与大气相通(以t=0.95 ms时刻为例), 在弹体进一步入水的过程中, 受到泡内外压强差的影响, 自由液面以上的空气不断涌入敞口空泡内部, 故此时空泡内的气体除了通入的气体之外还包括自然涌入的空气。对比4种不同通气工况下的空泡最大直径, 如表 1所示。
不同通气条件下空泡最大直径
除开口空泡阶段(0.45 ms)的最大空泡直径无较大差异外, 其他时刻入水空泡最大直径都与通气率呈正相关, 不同通气率下的空泡直径之间差值较大, 最大可达0.316D, 促使空泡直径增加了25%, 表明在这一阶段通气量越大, 空泡的径向尺寸越大, 排开的水越多。
在水的静压力、重力作用和空泡内壁的液体表面张力影响下, 入水初期弹体向四周所排开的水回流, 阻碍外部空气涌入, 导致空泡闭合于弹体后方表面。通气量对空泡的闭合有显著影响, 径向的通气可以持续排开弹体周围的水, 减缓水的回流, 因此较大的通气量可延缓空泡闭合。当空泡闭合后, 由于通气孔持续通气, 气流的惯性使得空泡内部仍然存在气体流动, 因此闭合后空泡的直径仍较大, 封闭空泡的体积也越大, 最大直径出现在自由液面以下。
随着入水深度的增加, 空泡的轴向尺寸被拉长, 受到空泡口处水流和气流的影响, 空泡内部压强较小, 自由液面喷溅的水在空泡内外压强差的作用下向中轴线处靠拢, 使得空泡顶部形成面闭合, 空气无法继续涌入空泡内部。发生面闭合后, 空泡内部在极短的时间内仍在继续膨胀, 此时空泡内部的压力下降, 自由液面以上的大气压对水下闭合的空泡顶端施加推力, 因此弹体持续向下运动时, 静水压力将空泡挤压, 并在水面形成水花喷出。
从空泡形态可以看出, 在通气量较大的情况下, 空泡的轴向和径向尺寸都较大。由于面闭合时自由液面以上的水向中间汇合的瞬间存在能量传递, 其动能转化后表现为闭合点处的射流现象, 向上的射流使得液面涌起窜高, 向下的射流汇集在弹体尾部, 使得空泡尾端形状类似“M”。对比以上4种工况下的自由液面可知, 通气量越大, 自由液面的涌起幅度较高, 射流现象明显。
3.2 通气量对空泡的闭合时间的影响
不同通气量下空泡的闭合时间有所差异, 仿真分析得到不同通气量下弹体以50 m/s入水过程中的闭合时间, 如表 2所示。
不同通气条件下空泡闭合时间
图 8给出了不同工况下闭合瞬间的泡内压强曲线, 弹体未入水时, 监测点位于大气中, 压强为101 325 Pa, 随着弹体运动、空泡的生成和发展, 监测点的压强发生变化。当入水0.8 ms后, 不通气的弹体表面空泡最先闭合, 仿真计算可知闭合空泡内部的压强为3 540 Pa, 已引起初始自然空化。
 |
图8 不同工况下空泡发展至闭合时泡内压强曲线 |
在空泡发展阶段, 泡内的气体主要来自于泡外空气和人工通气, 气体越多, 泡内压强越大, 通气量增加79%, 泡内压强增大11.5%。对比图 9几种工况在这一时刻的压强可知, 闭合空泡的泡内压强最小。由于空泡闭合主要受静水压和泡内压力不足的影响, 空泡内部的压力降越大, 空泡闭合越早, 通气量对泡内压强有显著影响, 通气量越大, 泡内压强越大, 使得空泡内外压强差越小, 进而导致自然空化数小, 促使空泡轴向和径向尺寸越大, 延迟空泡闭合现象的发生。
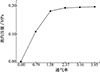 |
图9 t=0.8 ms时不同通气条件下泡内压强曲线 |
4 结论
建立了高速入水流场非定常数值模型, 分析了通气量变化对超空泡生成和演化过程的影响, 研究了泡内气体流动特性, 探讨了通气空化对空泡闭合的影响。主要结论如下:
1) 通气有利于入水空泡的生成和发展并会改变泡内气体流动特性。肩部通气能够促使泡内气体流动, 在肩部以下位置回旋产生气体小漩涡, 使得气体持续流动并拉长空泡, 因此通气条件下入水空泡的轴向和径向尺寸都比未通气时大。
2) 在入水初期空泡闭合前, 人工通气对空泡形态的影响不大, 空泡最大直径差值在0.015D以内; 随着航行体进一步入水, 通气段在自由液面以下, 通气工况与不通气相比, 空泡尺寸差别可达0.32D, 空泡直径增加了25%, 空泡尺寸随通气量的增加而增大。
3) 在空化器后方通入不凝气体可使得入水空泡闭合延迟, 通气量越大, 空泡闭合时间越长。不通气时入水空泡在0.8 ms闭合, 通气率为2.37, 空泡3.2 ms闭合, 通气率为4.74, 空泡4 ms闭合, 可见通气量增加1倍, 空泡闭合时间在原来的基础上可延迟25%。
References
- WORTHINGTON ACOLE R. Impact with a liquid surface, studied by the aid of instantaneous photography[J]. Philosophical Transactions of the Royal Society a Mathematical Physical and Engineering Sciences, 1997, 5: 137–148 [Google Scholar]
- MIRZAEI MALISHAHI MEGHTESAD M. High-speed underwater projectiles modeling: a new empirical approach[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2015, 37(2): 613–626 [Article] [Google Scholar]
- HUANG HongxinZHANG HuisuoWEI Jin, et al. Stability analysis of high-speed water entry of different structure projectiles[J]. Journal of Ordnance Equipment Engineering, 2019, 40(11): 50–54 (in Chinese) [Google Scholar]
- YU KZHANG GZHOU J, et al. Numerical study of the pitching motions of supercavitating vehicles[J]. Journal of Hydrodynamics, 2012, 24(6): 951–958 [Article] [Google Scholar]
- SHI H HTAKAMI T. Some progress in the study of the water entry phenomenon[J]. Experiments in Fluid, 2001, 30(4): 475–477 [Article] [Google Scholar]
- TRUSCOTT TTECHET A. A spin on cavity formation during water entry of hydrophobic and hydrophilic spheres[J]. Physics of Fluids, 2009, 21(12): 1–4 [Google Scholar]
- TRUSCOTT T, BEAL D, TECHET A. Shallow angle water entry of ballistic projectile[C]//Proceedings of the 7th International Symposiumon Cavitation, 2009: 17–22 [Google Scholar]
- ZOU ZhihuiLI JiaYANG Mao, et al. Experimental investigation on cavity flow characteristics of water entry of vehicle with gas jet cavitator[J]. Journal of Ballistics, 2022, 34(1): 1–8 (in Chinese) [Google Scholar]
- ZHAO HairuiSHI YaoPAN Guang. Numerical simulation of cavitation characteristics in high speed water entry of headjetting underwater vehicle[J]. Journal of Northwestern Polytechnical University, 2021, 39(4): 810–817 [Article] (in Chinese) [Google Scholar]
- CHEN ChengYUAN XulongREN Yao, et al. Experimental study on influence of ventilation on trajectory characteristics of free motion of supercavitating vehicle[J]. Journal of Northwestern Polytechnical University, 2019, 37(4): 691–696 [Article] (in Chinese) [Google Scholar]
- CAO WeiWEI YingjieHAN Wanjin, et al. Simulation of the trajectory stability of natural supercavitating vehicles[J]. Journal of Harbin Institute of Technology, 2012, 44(1): 26–30 (in Chinese) [Google Scholar]
- LUO KaiZUO ZhenhaoXU Haiyu, et al. Numerical simulation of the hysteresis characteristics of ventilated supercavity with high Froude number[J]. Journal of Harbin Engineering University, 2022, 43(4): 495–502 (in Chinese) [Google Scholar]
- GU JianxiaoDANG JianjunHUANG Chuang, et al. Influence of weight parameters on the effective range of supercavitation projectile[J]. Acta Armamentarii, 2022, 43(6): 1376–1386 (in Chinese) [Google Scholar]
- HUANG Chuang. Research of trajectory characteristics of supersonic-supercavitating projectiles[D]. Xi'an: Northweatern Polytechnical University, 2017 (in Chinese) [Google Scholar]
- XU HaiyuLUO KaiHUANG Chuang, et al. Influence of flow field's radial dimension on ventilated supercavitating flow[J]. Journal of Northwestern Polytechnical University, 2020, 38(3): 478–484 [Article] (in Chinese) [Google Scholar]
- GUO Zitao. Research on characteristics of projectile water entry and ballistic resistance of targets under different madiums[D]. Harbin: Harbin Institute of Technology, 2012 (in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 计算域及边界条件 |
| In the text | |
 |
图2 航行器附近的网格划分情况 |
| In the text | |
 |
图3 不同网格量的空泡轮廓对比图 |
| In the text | |
 |
图4 试验与数值仿真结果对比 |
| In the text | |
 |
图5 不同通气率的入水空泡形态演变图 |
| In the text | |
 |
图6 泡内气体速度矢量与压强叠加图 |
| In the text | |
 |
图7 系列通气率仿真结果对比 |
| In the text | |
 |
图8 不同工况下空泡发展至闭合时泡内压强曲线 |
| In the text | |
 |
图9 t=0.8 ms时不同通气条件下泡内压强曲线 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


