| Issue |
JNWPU
Volume 39, Number 4, August 2021
|
|
|---|---|---|
| Page(s) | 810 - 817 | |
| DOI | https://doi.org/10.1051/jnwpu/20213940810 | |
| Published online | 23 September 2021 | |
Numerical simulation of cavitation characteristics in high speed water entry of head-jetting underwater vehicle
头部喷气航行器高速入水空泡特性数值分析
1
School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China
2
Key Laboratory of Unmanned Underwater Vehicle Technology of Ministry of Industry and Information Technology, Xi’an 710072, China
Received:
20
October
2020
Autonomous underwater vehicle will be subjected to a huge impact load during high speed water entry, which will damage the structure and the internal instruments of the vehicle. Therefore, it is of great significance to study the buffer mechanism of the vehicle during the process of water-entry. In this paper, a kind of head-jetting device with disk cavitation is used. The complex cavitation forms, under the three-phase coupling of gas, liquid and solid, in the water entry process of the vehicle on which the device is installed. In this paper, the numerical simulation of high-speed water entry of the vehicle equipped with head jet device is carried out. Through the analysis of water entry cavitation under typical working conditions, the following conclusions are obtained. After the installation of head jet device, the water entry cavity of the vehicle changes gradually from cone to spindle shape. The air jet, compared with that without jet, can promote the formation of water inlet supercavitation, decrease the interaction area between the vehicle and water, and reduce the impact load during water entry. At the same water entry depth, the diameter of cavitation increases with the amount of air jet. The water entry velocity has a great influence on the difference of cavitation shape. The water entry depth closure phenomenon, when the water entry velocity is less than 100 m/s, can be observed in the depth of 3.5 times of the projectile length. The water entry angle has a significant effect on the cavitation shape. The cavity shows obvious asymmetry when the vehicle slants into the water, and the diameter and length of the bubbles decrease with the increase of the water entry angle. The research content of this paper provides technical support for the engineering practice of high-speed water entry and load reduction, and the conclusions are of great significance in related fields.
摘要
航行器在高速入水的过程中会受到巨大的冲击载荷作用,它会破坏航行器结构并损坏内部仪器,因此开展航行器入水缓冲机理的研究是很有意义的。使用一种带圆盘空化器的头部喷气装置,在气液固三相耦合下,航行器入水过程产生了复杂的空泡形态。开展了加装头部喷气装置的航行器高速入水数值模拟研究,通过对典型工况下入水空泡的分析,得到如下结论:加装头部喷气装置后航行器入水空泡由锥形逐渐变化为纺锤形;与不喷气时相比,喷气可促进入水超空泡的生成,减小入水过程中航行器与水的作用面积,降低该过程中的冲击载荷;同一入水深度下,空泡直径随喷气量而增大。入水速度对空泡形态差异性影响较大,其中入水速度100 m/s以下时可在3.5倍弹长的入水深度内观察到入水深闭合现象。入水角对空泡形态有明显影响,斜入水时空泡呈现明显不对称性,且空泡直径与长度随入水角增大而减小。研究内容为航行器高速入水降载的工程实际提供了技术支持,所得结论在相关领域具有重要意义。
Key words: numerical simulation / underwater vehicle / water entry / cavitation / head-jetting
关键字 : 数值模拟 / 航行器 / 入水 / 空泡 / 头部喷气
© 2021 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
航行器在投放过程中, 常涉及到跨越气液交界面的过程, 当航行器以高速入水时, 会受到巨大的冲击载荷作用并伴随着复杂的空泡形态, 将对航行器的物理结构、内部仪器和入水弹道等造成不可忽视的影响。因此, 国内外学者从理论、试验和数值模拟方面对该问题开展了大量的研究。
入水冲击载荷方面。理论研究多基于势流理论开展, 最早由von Karman[1]提出了近似平板理论, 这成为后来很多学者研究相关问题的理论依据。但是该理论忽略了液面隆起现象的影响, 之后Wagner[2]对其进行改进提出了自相似解法, 得到了入水冲击压强峰值与速度平方成正比的结论。Pukhnachov[3]提出了匹配渐进展开法来研究非线性因素在入水问题中的影响。Chuang[4-5]对平底物体入水开展了试验研究, 发现了空气垫的存在。陈震等[6]通过数值模拟, 也得出了空气垫在平底物体入水冲击中具有重要作用的结论。
入水空泡方面。Logvinovich[7]基于能量守恒定律提出了空泡独立扩张原理, 能够对空泡形态进行理论预报。Duclaux等[8]基于Besant-Rayleigh气泡平衡理论推导了入水空泡半径与时间的函数关系, 得到了与试验结果吻合较好的结果。Worthington等[9]最早用闪光照相机开展了球体垂直入水的试验研究, 并对其空泡形态进行了观测和描述。Bell[10]和Maccoll[11]通过对入水空泡试验进行观测, 总结了空泡生成和演化过程中的流动特征, 并分析了空泡的形成机理。马庆鹏等[12]通过求解雷诺时均的纳维斯托克斯方程, 开展了锥头圆柱体高速垂直入水的数值模拟研究, 得到了不同锥角头型与入水弹道和空泡半径等流场特性间的关系。
由上文可知, 冲击载荷和空泡特性是入水过程重要的研究内容, 而航行器高速入水又延伸出降载方案这一重要研究内容。通过优化航行器结构外形可以降低冲击载荷。此外,头部喷气形成气垫也可降低入水载荷, 潘龙等[13]开展了直径为16.74 mm的平头圆柱体垂直入水数值模拟研究, 采用头部直接射流的方法, 延长了结构物与水面间空气垫的作用时间, 得到了喷气可以减小入水冲击载荷的结论。刘华坪等[14]开展了不同喷气量和入水速度对于冲击载荷影响的数值模拟研究, 得到了增大喷气量可增强降载效果以及入水初速增大后降载效果减弱的结论。但是头部直接射流的方法存在一定的局限性, 在航行器高速入水时需要的喷气量过大, 难以在工程实际中应用。本文设计了带圆盘空化器的头部喷气装置, 通过圆盘空化器和喷气的共同作用, 使航行器在高速入水时产生包裹航行器的超空泡, 延长航行器与空气的作用时间, 以减小航行器入水过程中受到的载荷, 同时与直接射流法相比可大大减小喷气量。
1 物理模型和计算方法
1.1 研究对象与数值方法
采用如图 1所示的计算模型, 模型质量215 kg, 质心位于距前端面2 m处, 垂直入水时的转动惯量为Ixx=131.124 kg·m2, Iyy=3.234 kg·m2, Izz=131.124 kg·m2。直径为324 mm,总长L为3 872 mm。其中, 头部喷气装置长1 200 mm, 前端带圆盘空化器, 圆盘空化器直径为72 mm, 在空化器后部开孔喷气, 促进超空泡的生成, 开孔直径为15 mm, 为了简化仿真模型, 喷气孔以环形代替圆孔。
使用商业软件Fluent 19.2开展仿真计算, 采用嵌套网格方法, 其中外域为结构化网格, 网格数量约430万。子域及模型采用非结构网格, 并在模型表面进行加密处理, 网格数量约70万。网格如图 2所示。采用VOF(volume of fluid)多相流模型, 以模拟高速入水和喷气过程中气液固三相耦合作用。空化模型采用Zwart-Gerber-Belamri模型, 湍流模型为标准k-ε模型。压力速度耦合方式采用Coupled算法, 采用一阶迎风格式对动量和能量方程进行离散。使用了六自由度动网格方法。
 |
图1 计算模型示意图 |
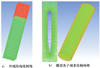 |
图2 计算网格 |
1.2 数值方法准确性验证
本文通过试验来对数值模拟方法的可靠性进行验证。首先根据相似理论对试验模型进行缩比, 头部喷气航行器入水主要包含了入水和喷气2个过程, 其中入水过程主要考虑重力、压力和惯性力的作用, 而喷气过程为孔口射流现象, 因此除几何相似外主要考虑了弗劳德相似
为适配试验室的空气炮发射装置, 取缩比后的模型直径为40 mm, 质量为0.5 kg。试验设计方案采用PU软管通气, 考虑到通气装置及发射装置的实际能力, 故取入水速度为10 m/s, 入水角90°, 喷气量0.98 g/s。然后使用已建立的数值方法开展了同一初始条件下的数值模拟, 如图 3所示, 得到了2.31 ms时刻的仿真空泡图和同一入水深度下的试验空泡形态。由空泡叠加图可知, 空泡曲线基本相吻合, 空泡直径在入水深度-25 mm处存在较大差值, 经计算, 该位置处的相对误差为5.1%。因此, 本文采用的数值方法可以较好地模拟头部喷气航行器的入水过程。
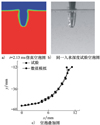 |
图3 空泡对比图 |
2 喷气量对入水空泡的影响
首先研究了喷气量对于头部喷气航行器入水空泡的影响, 其中入水角为90°, 入水速度200 m/s。图 4为不喷气时航行器在该初始条件下不同时刻的入水空泡形态演变图。在入水初期, 空泡为近似锥形, 随着入水深度的增加, 液面处逐渐收缩并隆起, 靠近液面处逐渐出现明显的纺锤形, 空泡中部受到水的挤压逐渐收缩。航行器主体前端在入水初期便出现明显的触水现象, 随着入水深度的增加, 触水面积逐渐增大。
图 5为喷气量4 kg/s时航行器的入水空泡形状演变图。由图可见,空泡形态和变化趋势基本与不喷气时相同。对比不喷气时的情况, 喷出的气体促进了入水超空泡的生成, 航行器主体在入水过程中没有触水, 从侧面说明, 喷气可以降低入水过程中的冲击载荷。
图 6为不同喷气量下的入水空泡叠加图, 其中喷气量分别为0, 2, 4, 8和16 kg/s。在入水初期, 航行器撞水和开空泡的阶段, 航行器前端空化器起主要作用, 入水空泡基本重合, 空泡最大直径位于水面处。随着入水深度的增加, 喷气的作用逐渐显现, 空泡直径随喷气量增大而增大, 且在液面以下靠近液面处空泡直径最大。
本文在航行器不同位置布置了压力监测点,如图 7所示。其中监测点1~3位于圆盘空化器前端面, 监测点4, 5位于喷气孔两侧, 监测点6位于头部喷气装置末端, 监测点7位于鳍舵上。通过对比各监测点的压强, 得到入水过程中航行器的压强分布及变化。
如图 8所示, 以喷气量4 kg/s时不同监测点的压强变化曲线为例。观察曲线并分析可知, 航行器垂直入水过程中, 由于空化器前端面持续与水接触,
位于空化器前端面的监测点1~3的压强较大, 并在入水瞬间达到峰值, 后迅速下降, 最终缓慢下行, 峰值脉宽短。监测点4~6处于超空泡中, 压强小, 曲线无明显波动。随着入水深度的增加, 鳍舵逐渐触水, 位于鳍舵处的监测点7压强曲线在30 ms左右开始上升, 并在一段时间后趋于平缓。综合比较得出, 入水过程中冲击压强最大区域位于空化器前端面的圆域内, 航行器主体处于超空泡包裹中, 冲击压强对其影响较小。
由上文可知, 航行器入水过程中只有监测点1, 2, 3和7有明显的压强变化, 因此下面将分别对比不同喷气量下监测点1, 2, 3和7压强曲线的变化, 分析喷气量的改变对于航行器所受冲击压强的影响。
图 9为不同喷气量下监测点1~3的压强变化曲线, 可以发现在入水初期的开空泡阶段, 空化器起主要作用, 因此不同喷气量下压强峰值基本相同, 随着入水深度的增加, 不同喷气量的差异性开始显现, 监测点压强随喷气量增大而减小, 说明增大喷气量可减小航行器入水过程中受到的冲击载荷。
图 10为鳍舵处监测点7的压强峰值随喷气量的变化曲线。观察曲线可推测得到, 喷气量的增加促进了入水超空泡的生成, 使鳍舵触水面积减小, 压强峰值降低, 减小了入水过程中航行器受到的载荷。
 |
图4 喷气量0 kg/s时空泡形状演变图 |
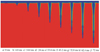 |
图5 喷气量4 kg/s时空泡形状演变图 |
 |
图6 不同时段、不同喷气量下空泡形态对比 |
 |
图7 压力监测点位置图 |
 |
图8 不同监测点压强对比(喷气量4 kg/s) |
 |
图9 不同喷气量下监测点1, 2和3压强对比 |
 |
图10 不同喷气量下监测点7压强峰值对比 |
3 初始速度对入水空泡的影响
本文同时研究了不同入水速度对于头部喷气航行器入水空泡的影响, 其中入水角为90°, 喷气量为4 kg/s, 入水速度为50~300 m/s。
图 11为同一入水深度下, 不同入水速度的空泡形态叠加图, 其中L为航行器总长。观察空泡形态可得, 入水深度为0.2L和1.2L时, 不同入水速度下空泡形态基本相同。随着入水深度的增加, 空泡形态出现较大差异, 入水速度为50和100 m/s, 在入水深度为2.2L时空泡中部出现明显的收缩段, 在入水深度3.5L时可观察到明显的空泡深闭合现象; 入水速度为150和200 m/s, 在入水深度3.5L时空泡中部才逐渐出现收缩现象; 入水速度为250和300 m/s时, 入水深度达到3.5L而空泡整体还在继续扩张。
在入水深度3.5L的范围内, 随着入水深度的增加, 空泡直径持续增大; 对比同一入水深度下不同入水速度的空泡直径可知, 空泡直径随入水速度增大而增大。
在入水深度3.5倍弹长、入水速度100 m/s以下时可观测到空泡深闭合现象, 因此下面将以100 m/s为典型工况, 分析喷气对于入水过程中航行器速度、加速度、受到的载荷及空泡的影响。
图 12为入水速度100 m/s时喷气与不喷气的航行器速度、加速度和压强云图对比。不喷气时, 速度曲线在40 ms左右出现明显突变, 对应了加速度曲线中该时刻迅速升高的趋势。对比49.5 ms时刻的压力云图, 发现不喷气时, 在航行器头部喷气装置末端出现高压区, 说明此时航行器主体已经触水, 空泡已在航行器前端闭合, 后续也不会出现空泡深闭合现象。而喷气促进了入水超空泡的生成, 持续喷出的气体将航行器主体与水隔开, 并在入水后期产生深闭合的空泡, 伴随航行器继续前进。49.5 ms后喷气的加速度值小于不喷气时的数值。证明了喷气可以有效减小入水过程中受到的载荷。
 |
图11 不同入水速度下空泡形态对比 |
 |
图12 入水初速100 m/s下喷气量为0和4 kg/s时航行器速度、加速度和压强云图对比 |
4 入水角度对入水空泡的影响
本文同时研究了不同入水角度对于头部喷气航行器入水空泡的影响, 其中入水速度100 m/s, 喷气量4 kg/s, 入水角度为60°~90°。
图 13为入水角60°时的入水空泡演变过程。如图所示, 在入水初期, 空泡为近似斜锥形, 液面出现隆起现象, 随入水深度增加, 空泡流中部开始收缩, 在约110 ms左右产生空泡深闭合, 空泡分成上下两部分, 上层近水面空泡为近似纺锤形, 在喷气作用下, 航行器携带下层空泡继续向下运动, 在水压作用下这部分空泡长度和直径逐渐减小。整个过程中空泡呈现明显的不对称性, 背水侧液面隆起程度大于迎水侧。产生空泡深闭合后, 上层近水面空泡的背水侧空泡膨胀大于迎水侧。在128.7 ms左右, 航行器前端迎水面触水, 航行器受力抬头, 168.3 ms左右, 航行器前端背水面触水, 航行器受力低头, 使航行器入水弹道发生偏移。
图 14为不同入水角度下的空泡形态对比。由图可知, 空泡最大直径随入水角增大而减小, 斜入水时空泡呈现非对称性, 且不对称程度随入水角减小而增大。在入水初期, 90°的空泡长度最大, 斜入水空泡长度接近。随入水深度的增加, 斜入水空泡长度逐渐增大, 且空泡长度随入水角减小而增大。
 |
图13 入水角60°时空泡形状演变图 |
 |
图14 不同入水角度下空泡形态对比 |
5 结论
本文采用数值模拟方法研究了加装头部喷气装置的航行器在高速入水过程中的空泡特性。得到的结论如下:
1) 加装头部喷气装置后, 空泡形态由入水初期的锥形逐渐变化为纺锤形, 并可观察到明显的液面隆起和中段收缩现象。
2) 航行器撞水和开空泡的阶段, 空化器起主要作用, 入水空泡基本重合, 冲击压强峰值基本相同, 随着入水深度的增加, 空泡直径随喷气量而增大, 且喷气促进了入水超空泡的生成, 减小了航行器触水面积, 降低了入水过程中的冲击载荷。
3) 航行器以不同初速垂直入水时, 入水初期, 空泡形态基本相同, 随着入水深度增加, 空泡形态出现明显差异, 其中入水速度100 m/s以下时可观察到空泡深闭合现象。
4) 航行器斜入水时, 空泡呈现明显的不对称性。当产生空泡深闭合后, 航行器出现局部触水现象并在受力作用下发生弹道偏移。
5) 对比不同入水角下的空泡形态, 空泡最大直径与斜入水时的不对称程度随入水角增大而减小, 在入水初期, 90°的空泡长度最大, 斜入水空泡长度接近。随着入水深度的增加, 斜入水的空泡长度逐渐增大, 且空泡长度随入水角增大而减小。
本文所得的相关结论, 可为航行器高速入水缓冲降载相关研究提供参考。
References
- Von Karman T. The impact on seaplane floats during landing[J]. 1929, 321: 1–9 [Google Scholar]
- Wagner H. Phenomena associated with impacts and sliding on liquid surfaces[J]. Math Mech, 1932, 12(4): 193215 [Article] [Google Scholar]
- Pukhnachov V V. Linear approximation in the problem on a blunt body entry in water[J]. Din Sploshnoi Sredy, 1979, 38: 143–150 [Google Scholar]
- Chuang S L. Experiments on flat-bottom slamming[J]. Journal of Ship Research, 1966, 10(1): 10–27 [Article] [CrossRef] [Google Scholar]
- Chuang S L. Experiments on slamming of wedge-shapes bodies[J]. Journal of Ship Research, 1967, 11(3): 190–198 [Article] [CrossRef] [Google Scholar]
- Chen Zhen, Xiao Xi. Simulation analysis on the role of air cushion in the slamming of a flat-bottom structure[J]. Journal of Shanghai Jiaotong University, 2005, 39(5): 670–673 [Article] (in Chinese) [Google Scholar]
- Logvinovich G V. Hydrodynamics of flows with free boundaries[M]. Kiev: Naukova Dumka Publishers, 1969 [Google Scholar]
- Duclaux V, Caillé F, Duez C, et al. Dynamics of transient cavities[J]. Journal of Fluid Mechanics, 2007, 591: 1–19 [Article] [Google Scholar]
- Worthington A M, Cole R S. Impact with a liquid surface studied by the aid of instantaneous photography[J]. Philosophical Transactions of the Royal Society, 1900, 194(A): 175–200 [NASA ADS] [Google Scholar]
- Bell Eric G. LXXVI on the impact of a solid sphere with a fluid surface and the influence of surface tension, surface layers, and viscosity on the phenomenon[J]. Philosophical Magazine, 1924, 48(287): 753–764 [Article] [Google Scholar]
- MacColl J W. Aerodynamics of a spinning sphere[J]. Royal Aeronautical Society Journal, 1928, 32: 777–798 [Article] [CrossRef] [Google Scholar]
- Ma Qingpeng, Wei Yingjie, Wang Cong, et al. Numerical simulation of high-speed water entry cavity of cylinders[J]. Journal of Harbin Institute of Technology, 2014, 46(11): 24–29 [Article] (in Chinese) [Google Scholar]
- Pan Long, Wang HuanRan, Yao Erren, et al. Mechanism research on the water-entry impact of the head-jetting flat cylinder[J]. Journal of Engineering Thermophysics, 2015, 36(8): 1691–1695 [Article] (in Chinese) [Google Scholar]
- Liu Huaping, Yu Feipeng, Han Bing, et al. Numerical simulation study on influence of top jet in object water entering impact[J]. Journal of Engineering Thermophysics, 2019, 40(2): 300–305 [Article] (in Chinese) [Google Scholar]
All Figures
 |
图1 计算模型示意图 |
| In the text | |
 |
图2 计算网格 |
| In the text | |
 |
图3 空泡对比图 |
| In the text | |
 |
图4 喷气量0 kg/s时空泡形状演变图 |
| In the text | |
 |
图5 喷气量4 kg/s时空泡形状演变图 |
| In the text | |
 |
图6 不同时段、不同喷气量下空泡形态对比 |
| In the text | |
 |
图7 压力监测点位置图 |
| In the text | |
 |
图8 不同监测点压强对比(喷气量4 kg/s) |
| In the text | |
 |
图9 不同喷气量下监测点1, 2和3压强对比 |
| In the text | |
 |
图10 不同喷气量下监测点7压强峰值对比 |
| In the text | |
 |
图11 不同入水速度下空泡形态对比 |
| In the text | |
 |
图12 入水初速100 m/s下喷气量为0和4 kg/s时航行器速度、加速度和压强云图对比 |
| In the text | |
 |
图13 入水角60°时空泡形状演变图 |
| In the text | |
 |
图14 不同入水角度下空泡形态对比 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


