Experimental study on the piezoelectric active vibration reduction system of wind tunnel aerodynamic models

Weiguang LI; Zhichun YANG; Ximing ZHU

doi:10.1051/jnwpu/20254310058

All issues

Volume 43 / No 1 (February 2025)

JNWPU, 43 1 (2025) 58-65

Full HTML

Open Access

Issue		JNWPU Volume 43, Number 1, February 2025


Page(s)		58 - 65
DOI		https://doi.org/10.1051/jnwpu/20254310058
Published online		18 April 2025

JNWPU 2025, 43(1): 58–65

Experimental study on the piezoelectric active vibration reduction system of wind tunnel aerodynamic models

风洞测力模型压电主动减振系统试验研究

Weiguang LI (李伟光)¹, Zhichun YANG (杨智春)² and Ximing ZHU (朱玺名)²

¹ School of Sciences, Chang'an University, Xi'an 710064, China
² School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China

Received: 28 February 2024

Abstract

During the wind tunnel model aerodynamic test, the slender cantilever model tail support system is susceptible to low-frequency and high-amplitude resonance caused by airflow separation and turbulence, which has a significant impact on test data quality. To effectively suppress the flow-induced vibration response of wind tunnel models, a hybrid control algorithm combining the filtered-x least mean square (FxLMS) algorithm and the linear active disturbance rejection control (LADRC) controller is proposed. Subsequently, the corresponding controller is designed to build a piezoelectric active vibration reduction system, and the active vibration control ground tests of the wind tunnel aerodynamic model are performed. The results show that the proposed hybrid control algorithm fully utilizes the advantages of the FxLMS algorithm and the LADRC controller, as well as having strong anti-disturbance performance, ensuring reliable measurement of the wind tunnel model aerodynamic characteristics.

摘要

在风洞模型测力试验时, 细长悬臂式模型-尾撑系统极易因气流分离和湍流而发生低频、大幅共振, 严重影响了测试数据质量。为了高效抑制风洞测力模型的流致振动响应, 提出了一种将自适应滤波算法和线性自抗扰控制器相结合的混合控制算法。设计相应的控制器搭建压电主动减振系统, 开展了风洞测力模型振动主动控制地面试验研究。结果表明, 所提混合控制算法充分发挥了自适应滤波算法和线性自抗扰控制器各自的优势, 并且具有很强的抗扰性, 保障了风洞模型气动特性的稳定测量。

Key words: wind tunnel test / active vibration control / piezoelectric stack actuator / FxLMS algorithm / LADRC algorithm

关键字 : 风洞试验 / 振动主动控制 / 压电叠堆作动器 / 自适应滤波算法 / 自抗扰控制

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

大型民航客机、军用运输机、战斗机和无人机等飞行器是航空航天领域的核心装备, 是国家经济、技术、国防和工业化发展程度的重要体现。在飞行器研制过程中, 必须对其在不同速压、各种飞行姿态下的空气动力学性能进行准确评估, 风洞试验即是获取飞行器气动性能数据的重要手段[1]。为了减小支撑系统对风洞测力模型气动特性的干扰, 尾部支撑(后文简称尾撑)结构是最为常用的支撑形式。然而, 在飞行器模型大攻角风洞试验工况下, 模型-尾撑系统极易因气流分离和湍流而产生剧烈振动, 严重影响了风洞模型气动性能数据的测试, 制约了新型飞行器的设计研发进程[2]。因此, 针对风洞模型流致振动这一重要问题, 开发1套高效、可靠的风洞模型尾撑结构减振系统, 对我国新一代飞行器的研制和型号飞行器的改进改型具有重要意义。

随着小体积、高负载、大标称推力压电叠堆作动器(后文简称压电作动器)的出现, 压电智能结构振动主动控制技术成为了风洞模型尾撑结构减振领域的研究热点, 该方法通过在尾撑结构上集成压电作动器, 利用传感器监测模型-尾撑系统的振动响应, 采取适宜的控制策略实时计算出控制电压, 驱动压电作动器对尾撑结构施加主动控制力或力矩, 从而达到消除结构振动响应的目的[1]。

目前世界上最先进的2座跨声速风洞——美国国家跨声速风洞(national transonic facility, NTF)和欧洲跨声速风洞(european transonic wind-tunnel, ETW), 在建设初期就开始了旷日持久的风洞模型主动减振方法研究, 投入了大量的人力和物力, 至今仍然没有完全解决[3–8]。早在1996年, ETW的Wimmel等[3]就提出了1种基于压电作动器的风洞模型减振方法, 研制了1套由环布的6根压电作动器组成的分体式压电主动减振结构。2001年, Fehren等[4]对Wimmel等的方案进行了改进, 并在ETW风洞中进行了试验验证, 使其成为第1代压电主动减振结构AVS-1。随后, ETW还陆续发展了2种电磁作动器驱动的减振结构AVS-2和AVS-3, 并与AVS-1配合使用, 进一步增强了风洞模型尾撑结构减振系统的抑振能力[5]。与此同时, 2005年, 美国国家航空航天局(national aeronautics and space administration, NASA)与ViGYAN公司的Balakrishna等合作, 提出了1种安装在支杆和天平之间的压电主动减振结构, 其将4根压电作动器分成2组, 分别控制飞行器模型垂直和水平方向上的振动响应。风洞试验结果表明, 该减振结构最高可抑制88%的模型振动响应[6]。2008年, Balakrishna等[7]又对前期方案进行了改进, 主要调整了压电作动器的分布以进一步增强其减振能力。此后, NTF针对不同模型的减振需求, 陆续开发了3套压电主动减振系统, 分别是Pathfinder Ⅰ模型减振系统、Crew Launch Vehicle(CLV)模型减振系统和Common Research Model(CRM)模型减振系统。在Pathfinder Ⅰ模型减振系统中, 4根压电作动器呈环形分布在支杆与天平之间, 该系统能够承受较大的静态载荷, 但其对于发散性振动的抑制效果不佳。在CRM模型减振系统中, 12根压电作动器被分成4组均匀布置在远离天平的位置, 在某跨声速风洞试验中, 该减振系统将飞行器模型的最大试验攻角从无减振系统时的6°提高到了12°。CLV模型减振系统与CRM模型减振系统类似, 也安装在支杆结构根部, NTF分别用比例为0.548%和1%的CLV模型来检验该系统对于同类而不同质量模型的减振能力, 并通过风洞试验证明了其具有一定的通用性[8]。

国内对于风洞模型尾撑结构主动减振方法的研究起步较晚, 但也在空气动力实验相关科研机构的努力下取得了一定成果。2012年, 南京航空航天大学沈星教授团队研制了1套适用于低速风洞模型的内嵌式压电主动减振结构, 同时设计比例积分微分(proportional integral derivative, PID)控制器使模型-尾撑系统的一阶弯曲模态振动响应衰减了19 dB以上[9]。此后, 该团队又陆续研制了1套跨声速风洞模型压电主动减振系统和1套多自由度压电主动减振系统[10–11]。2015年, 大连理工大学刘巍教授团队提出了1种外套式压电主动减振结构, 并基于PD控制器开展了风洞模型振动主动控制地面试验研究, 实现了约75%的减振效果[12]。2018年, 该团队又在沈阳1.2 m跨超声速风洞研制了1套支杆根部内嵌式压电主动减振系统, 跨声速风洞试验结果表明, 该系统可以有效抑制风洞模型的多维激变振动响应[2]。

现有的风洞模型尾撑结构压电主动减振系统大多基于PID控制器开发而来, 而复杂的风洞试验工况对控制系统的快速性、准确性、适应性和抗扰性均提出了更高的要求。PID控制器的结构设计和参数整定十分依赖于人工经验和现场调试, 同时, 固定参数的PID控制器往往针对单一模型和单一工况控制效果较好, 难以满足风洞模型减振应用中同一模型连续变工况以及不同模型单一或连续变工况的减振需求[13]。自适应滤波算法(filtered-x least mean square, FxLMS)因具有收敛性好、适应性强、不依赖于被控系统精确数学模型等优势, 成为当下结构振动主动控制算法的研究热点之一[14]。然而, 传统FxLMS算法在收敛速度与收敛精度等方面与步长的调整相互矛盾, 且在算法运行过程中需要预知与外扰信号相关的参考信号。为了克服传统FxLMS算法所固有的局限性, Li等[15]提出1种将反馈FxLMS算法和PID控制器相结合的PID-FxLMS混合控制算法, 并基于此开展了压电悬臂梁振动主动控制试验研究, 结果表明, 所提PID-FxLMS混合控制算法的收敛速度和抑振效果均优于单独使用传统FxLMS算法或PID控制器。此外, 针对PID控制器存在的参数依赖性强、抗扰性差和控制系统快速性与超调量无法兼顾等问题, 高志强等[16]提出了1种不依赖于被控系统模型的线性自抗扰控制器(linear active disturbance rejection control, LADRC), LADRC控制器继承了PID控制的精髓, 即“基于误差来消除误差”, 并克服了参数依赖性强、抗扰性差等缺点, 具有鲁棒性强, 控制精度高、速度快且控制耗能等优势。

因此, 在上述研究基础上, 本文将反馈FxLMS算法与LADRC控制器相结合, 进一步提出了1种新型LADRC-FxLMS混合控制算法, 以充分发挥2种算法各自的优势。随后, 采用子空间辨识方法离线辨识得到了控制通道模型, 并设计相应的控制器搭建压电主动减振系统开展了风洞测力模型振动主动控制地面试验研究, 验证了所提方法的高效性和抗扰性。

1 LADRC-FxLMS混合控制算法

1.1 反馈FxLMS算法

传统FxLMS算法通常由两部分组成: 有限脉冲响应(finite impulse response, FIR)滤波器和最小均方(least mean square, LMS)自适应算法, 自适应算法通过在线调节滤波器的权系数, 以提高其信号处理能力。传统FxLMS算法需要预知与外扰信号相关的参考信号, 而在风洞试验中, 很难提前获取外扰信号并将其作为参考信号输入控制算法。针对这一问题, 结合FxLMS算法的迭代过程, 研究人员直接从结构振动响应中提取参考信号, 并由此构建了基于参考信号重构的反馈FxLMS算法[15], 如图 1所示。图 1中, x(n)为外扰信号; y′(n)为n时刻的振动控制量, 它是由控制输出y(n)经过控制通道H(z)后得到的; e(n)为n时刻的结构振动响应误差信号; 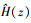为控制通道模型, 一般可由离线辨识得到, x′(n)为外扰x(n)经过控制通道模型后给滤波器的输入信号。d(n)为不施加控制信号时n时刻的结构振动响应, 实际应用中往往难以获得, 如果控制通道模型足够准确, 那么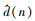是对d(n)一个很好的估计。同时, 如果初级通道P(z)是一个线性结构, 则外扰信号与d(n)也线性相关, 那么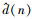和外扰信号也是线性相关的。基于参考信号重构的反馈FxLMS算法迭代过程为：

图1

反馈FxLMS算法框图

式中: X ′(n)是长度为L的滤波器输入信号矢量; W (n)为n时刻滤波器的N个权系数值; μ为算法步长, 决定算法的收敛速度与收敛精度。FxLMS算法的收敛条件为[17]

式中, λ_max为滤波器输入信号自相关矩阵的最大特征值。

1.2 LADRC-FxLMS混合控制算法

由(1)式可知, 合理选择LMS算法步长对FxLMS算法的收敛速度、收敛精度和稳定性尤为重要。步长越小, 算法的稳定性和收敛精度越高, 但滤波器的权系数迭代更新速度越慢, 导致控制系统在相当长的一段时间内都无法实现令人满意的控制效果; 步长越大, 滤波器权系数的更新速度越快, 但若长时间保持较大步长运行, 控制系统的稳定性会降低, 甚至会引起控制发散。

考虑到LADRC控制器和反馈FxLMS算法虽然在结构形式上大有不同, 但是从控制器的输入和输出信号来看, 其均是以被控结构的误差信号作为输入, 并通过计算输出控制信号以驱动作动器对结构施加控制力或力矩, 从而实现结构振动响应的主动控制。因此, 本文提出了1种将反馈FxLMS算法与LADRC控制器相结合的LADRC-FxLMS混合控制算法, 旨在充分发挥2种算法各自的优势, 提升风洞模型压电主动减振系统的抑振效果。

仅考虑模型垂直方向的风洞模型尾撑结构振动方程可以表示为[18]

式中：m, c和k分别为系统的质量、阻尼和刚度; W为作用在系统上的气动载荷; b为压电驱动增益; u为压电作动器的驱动电压。将(3)式两边同时除以m, 并进一步整理得到

式中，c′=c/m, k′=k/m, W′=W/m且b′=b/m。考虑到压电作动器所固有的迟滞非线性, 将b′简化为线性增益时难免引入误差, 假设其线性增益部分为b₀, 则

f为系统的总扰动。由此, 即可分别设计线性扩张状态观测器(linear extended state observer, LESO)和线性状态误差反馈控制律(linear state error feedback, LSEF)来构成LADRC控制器[16]。

式中: 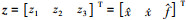为观测器的状态向量; 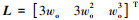为误差反馈增益矩阵, w_o为LESO的带宽; k_p和k_d为LSEF的参数, 可以设置为k_p=w_c², k_d=2w_c, w_c为LSEF的带宽, U_LADRC是LADRC控制器输出的控制信号。

将反馈FxLMS算法与所设计的LADRC控制器相结合, 即可构造出LADRC-FxLMS混合控制算法, 算法框图如图 2所示。图中U_LMS(n)和U_LADRC(n)分别是n时刻反馈FxLMS算法和LADRC控制器输出的控制信号, U(n)为混合控制算法的输出信号。LADRC-FxLMS混合控制算法的计算过程为

图2

LADRC-FxLMS混合控制算法框图

2 振动主动控制地面试验

在设计压电主动减振系统时, 压电作动器的安装位置会显著影响减振系统效能。由压电主动控制系统的模态应变能准则可知: 将压电作动器布置于受控目标模态最大应变能处即可有效抑制目标模态的振动响应[19]。对于风洞模型尾撑结构来说, 如图 3所示, 其主要受控目标模态为整体系统的一阶弯曲模态[9], 对应的模态应变能最大处在支杆结构的根部。因此, 本文将压电作动器布置在支杆结构根部来设计风洞模型尾撑结构压电主动减振系统。

图3

典型风洞模型尾撑系统

2.1 控制通道离线辨识

由反馈FxLMS算法可知, 为了抑制观测点的振动响应, 需要利用控制通道模型来驱动自适应算法, 并实时重构出参考信号以产生与原振动响应信号反相的控制信号y′(n)将其抵消。因此, 控制通道模型辨识是FxLMS控制器设计中非常重要的一个环节, 辨识结果的准确性会直接影响控制效果和系统的稳定性。本文采用N4SID(numerical algorithm for subspace state space system identification)子空间辨识方法, 通过采集控制通道的输入输出数据, 辨识得到控制通道的状态空间模型[20]。

控制通道辨识实验系统框图如图 4所示, 首先在dSPACE实时控制仿真系统中搭建信号发生器模块, 产生6~16 Hz偏置为500 V的步进正弦扫频信号并实时记录, 随后经dSPACE输出板卡D/A转换后, 输入压电功放, 驱动压电作动器对底部固支的风洞模型尾撑结构压电主动减振系统进行激励。尾撑结构在垂直方向上的振动响应由粘贴在支杆等直段根部的应变片S_y测量, 并通过动态应变放大器放大后输入到采集板卡, 经A/D转换得到结构的振动响应信号。

图4

控制通道辨识系统框图

基于测量得到的控制通道输入电压信号和输出应变信号, 采用Matlab/System Identification工具箱的N4SID子空间辨识算法, 辨识控制通道的状态空间模型。辨识结果如图 5所示(其中50~65 s辨识结果放大显示), 可以看到, 控制通道模型的辨识精度均在99%以上, 在关心频带内, 辨识模型频响函数的幅频特性和相频特性都能很好地与试验测试曲线吻合, 可以用于控制器的设计。

图5

控制通道辨识结果

2.2 振动主动控制地面试验验证

2.2.1 地面试验系统

风洞模型尾撑结构流致振动问题的本质, 是整体结构系统因气流分离和湍流而发生的共振, 是一种抖振现象[1]。为了模拟压电主动减振系统的实际工况, 将所设计的风洞模型尾撑结构压电主动减振系统固定在振动台上, 由振动台产生整体系统一阶弯曲模态频率处(11.75 Hz)的谐波基础激励, 激发其共振现象。

振动主动控制地面试验现场布置如图 6所示, 所采用的仪器设备信息如表 1所示。其中, 尾撑结构在垂直方向上的振动响应由粘贴在支杆等直段根部的应变片S_y测量, 并通过动态应变放大器放大后输入到采集板卡作为控制反馈信号。在dSPACE实时控制仿真系统中搭建相应的控制器, 实时计算出控制电压信号, 再通过输出板卡输出至压电功放, 经放大后, 驱动压电作动器对支杆结构施加控制力和力矩, 从而实现风洞模型尾撑结构振动的主动控制。此外, 采用安装在飞行器模型重心处的加速度传感器A_y监测其在垂直方向上的振动响应, 并通过加速度信号调理器输入采集板卡并实时记录, 作为风洞模型减振效果的衡量指标。

图6

振动主动控制地面试验现场布置

表1

实验仪器设备信息

2.2.2 试验验证结果

采用上述振动主动控制地面试验系统, 来对比研究所提LADRC-FxLMS混合控制算法相较于反馈FxLMS算法和LADRC控制器的优越性, 各控制器参数设置如表 2所示。

表2

控制器参数设置

振动主动控制地面试验结果如图 7所示, LADRC-FxLMS混合控制器充分发挥了LADRC控制器和反馈FxLMS算法各自的优势, 最终减振效果达到了92.66%, 而收敛时长仅为1.29 s, 相较于FxLMS控制器, 收敛时长缩短了17.89 s; 相较于LADRC控制器, 最终减振效果提升了1.06%。进一步探究其原因, 各控制器的控制电压如图 8所示, 混合控制器在控制初期输出的控制电压明显高于FxLMS控制器, 从而大幅提升了反馈FxLMS算法的收敛速度; 同时, 随着滤波器权系数的逐步更新, 混合控制器的控制电压逐渐趋近于最优值, 提升了LADRC控制器的收敛精度。

图7

振动主动控制试验结果

图8

各控制器的控制电压

此外, 考虑到风洞试验环境及各种仪器设备均会不可避免地引入噪声干扰, 实际结构的振动响应通常不是纯谐波信号。为了进一步检验所提LADRC-FxLMS混合控制器抵抗噪声干扰的能力, 开展在误差反馈信号中添加幅值为原振动响应信号10%的6~16 Hz窄带随机信号工况下的振动主动控制试验研究, 控制器参数设置与表 2保持一致。

抗扰性试验结果如图 9所示, 在叠加模拟噪声干扰工况下, 混合控制器依然能够在1.02 s内将观测点的加速度响应均方根值降低92.77%。最终, 风洞模型尾撑结构加速度响应的功率谱密度(power spectral density, PSD)曲线峰值下降了47.57 dB, 优于LADRC控制器和FxLMS控制器, 验证了本文所提LADRC-FxLMS混合控制算法具有很强的抗扰性。

图9

抗扰性试验结果

3 结论

针对风洞测力模型流致振动的主动控制问题, 本文提出了1种将反馈FxLMS算法与LADRC控制器相结合的LADRC-FxLMS混合控制算法。随后, 采用N4SID子空间辨识方法离线辨识得到了控制通道模型, 并设计相应的控制器搭建压电主动减振系统开展了风洞测力模型振动主动控制地面试验研究。结果表明, 所提LADRC-FxLMS混合算法充分发挥了2种算法各自的优势, 收敛速度明显加快且稳态误差更小。最终, 风洞模型尾撑结构的振动响应降低了92%以上, 有效提升了压电主动减振系统效能, 并且具有很强的抗扰性。

References

ZHANG LeiJIANG ShuaiheHUANG Yun, et al. A review of active vibration control for full span models in wind tunnels based on piezoelectric actuators[J]. Chinese Journal of Applied Mechanics, 2022, 39(4): 607–616 (in Chinese) [Google Scholar]
LIU WZHOU MWEN Z, et al. An active damping vibration control system for wind tunnel models[J]. Chinese Journal of Aeronautics, 2019, 32(9): 2109–2120 [Google Scholar]
WIMMEL R, FEHREN H, GNAUERT U, et al. 5 DOF active vibration control with a piezoceramic driven multifunctional interface for high load application[C]//Seventh International Conference on Adaptive Structures, Lancaster, 1997: 61–70 [Google Scholar]
FEHREN H, GNAUERT U, WIMMEL R, et al. Validation testing with the active damping system in the european transonic wind-tunnel[C]//39th Aerospace Sciences Meeting and Exhibit, 2001 [Google Scholar]
SCHIMANSKI D, QUEST J. Flight Reynolds number testing: the european project FLIRET[C]//47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 2009 [Google Scholar]
BALAKRISHNA S, HOULDEN H, BUTLER D, et al. Development of a wind tunnel active vibration reduction system[C]//45th AIAA Aerospace Sciences Meeting and Exhibit, 2007 [Google Scholar]
BALAKRISHNA S, BUTLER D, WHITE E, et al. Active damping of sting vibrations in transonic wind tunnel testing[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, 2008 [Google Scholar]
RIVERS M B, BALAKRISHNA S. NASA common research model test envelope extension with active sting damping at NTF[C]//32nd AIAA Applied Aerodynamics Conference, 2014 [Google Scholar]
SHEN XingTU FanfanCHEN Jinjin, et al. Study of active damping system for the cantilever sting in wind tunnel based on piezoelectric actuators[J]. Journal of Vibration, Measurement&Diagnosis, 2014, 34(3): 414–419 (in Chinese) [Google Scholar]
SHEN XDAI YCHEN M, et al. Active vibration control of the sting used in wind tunnel: comparison of three control algorithms[J]. Shock and Vibration, 2018, 2018(1): 1905049 [Article] [Google Scholar]
YU YSHEN XHUANG Y. Multidimensional system identification and active vibration control of a piezoelectric-based sting system used in wind tunnel[J]. Shock and Vibration, 2020, 2020(1): 8856084 [Google Scholar]
LIU WeiBI XiaodanJIA Zhenyuan, et al. Design and experiment on active damper of wind-tunnel model[J]. Optics and Precision Engineering, 2015, 23(10): 2895–2901 (in Chinese) [Google Scholar]
ZHANG ShuyangZHANG ShunqiLI Jing, et al. Shape control and active vibration control of piezoelectric smart structures with PID algorithm[J]. Journal of Northwestern Polytechnical University, 2017, 35(1): 74–81 [Article] (in Chinese) [Google Scholar]
LI WeiguangYANG ZhichunZHU Ximing, et al. Piezoelectric adaptive active vibration suppression for wind-tunnel model support sting[J]. Smart Materials and Structures, 2024, 33(8): 085020 [Article] [Google Scholar]
LI WeiguangYANG ZhichunLI Kui, et al. Hybrid feedback PID-FxLMS algorithm for active vibration control of cantilever beam with piezoelectric stack actuator[J]. Journal of Sound and Vibration, 2021, 509: 116243 [Article] [Google Scholar]
GAO Z Q, AAC A C. Scaling and bandwidth-parameterization based controller tuning[C]//Annual American Control Conference, Denver, 2003 [Google Scholar]
NIU WZOU CLI B, et al. Adaptive vibration suppression of time-varying structures with enhanced fxlms algorithm[J]. Mechanical Systems and Signal Processing, 2019, 118: 93–107 [Article] [Google Scholar]
LI WeiguangYANG ZhichunLIU Ke, et al. Piezoelectric active disturbance rejection control for flow-induced vibration of the wind tunnel test models[J]. Mechanical Systems and Signal Processing, 2025, 224: 112010 [Article] [Google Scholar]
LI BinLI YugangYIN Xuegang, et al. The modal force rule of point piezoelectric actuator place optimization on intelligent beam and frame[J]. Chinese Space Science and Technology, 20001): 3–7 (in Chinese) [Google Scholar]
LIANG Li. Study on active control of vertical tail buffet with piezoelectric actuators[D]. Xi'an: Northwestern Polytechnical University, 2016 (in Chinese) [Google Scholar]

All Tables

实验仪器设备信息

控制器参数设置

All Figures

	图1 反馈FxLMS算法框图
In the text

	图2 LADRC-FxLMS混合控制算法框图
In the text

	图3 典型风洞模型尾撑系统
In the text

	图4 控制通道辨识系统框图
In the text

	图5 控制通道辨识结果
In the text

	图6 振动主动控制地面试验现场布置
In the text

	图7 振动主动控制试验结果
In the text

	图8 各控制器的控制电压
In the text

	图9 抗扰性试验结果
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] ZHANG LeiJIANG ShuaiheHUANG Yun, et al. A review of active vibration control for full span models in wind tunnels based on piezoelectric actuators[J]. Chinese Journal of Applied Mechanics, 2022, 39(4): 607–616 (in Chinese) [Google Scholar]

[2] LIU WZHOU MWEN Z, et al. An active damping vibration control system for wind tunnel models[J]. Chinese Journal of Aeronautics, 2019, 32(9): 2109–2120 [Google Scholar]

[3] WIMMEL R, FEHREN H, GNAUERT U, et al. 5 DOF active vibration control with a piezoceramic driven multifunctional interface for high load application[C]//Seventh International Conference on Adaptive Structures, Lancaster, 1997: 61–70 [Google Scholar]

[4] FEHREN H, GNAUERT U, WIMMEL R, et al. Validation testing with the active damping system in the european transonic wind-tunnel[C]//39th Aerospace Sciences Meeting and Exhibit, 2001 [Google Scholar]

[5] SCHIMANSKI D, QUEST J. Flight Reynolds number testing: the european project FLIRET[C]//47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 2009 [Google Scholar]

[6] BALAKRISHNA S, HOULDEN H, BUTLER D, et al. Development of a wind tunnel active vibration reduction system[C]//45th AIAA Aerospace Sciences Meeting and Exhibit, 2007 [Google Scholar]

[7] BALAKRISHNA S, BUTLER D, WHITE E, et al. Active damping of sting vibrations in transonic wind tunnel testing[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, 2008 [Google Scholar]

[8] RIVERS M B, BALAKRISHNA S. NASA common research model test envelope extension with active sting damping at NTF[C]//32nd AIAA Applied Aerodynamics Conference, 2014 [Google Scholar]

[9] SHEN XingTU FanfanCHEN Jinjin, et al. Study of active damping system for the cantilever sting in wind tunnel based on piezoelectric actuators[J]. Journal of Vibration, Measurement&Diagnosis, 2014, 34(3): 414–419 (in Chinese) [Google Scholar]

[10] SHEN XDAI YCHEN M, et al. Active vibration control of the sting used in wind tunnel: comparison of three control algorithms[J]. Shock and Vibration, 2018, 2018(1): 1905049 [Article] [Google Scholar]

[11] YU YSHEN XHUANG Y. Multidimensional system identification and active vibration control of a piezoelectric-based sting system used in wind tunnel[J]. Shock and Vibration, 2020, 2020(1): 8856084 [Google Scholar]

[12] LIU WeiBI XiaodanJIA Zhenyuan, et al. Design and experiment on active damper of wind-tunnel model[J]. Optics and Precision Engineering, 2015, 23(10): 2895–2901 (in Chinese) [Google Scholar]

[13] ZHANG ShuyangZHANG ShunqiLI Jing, et al. Shape control and active vibration control of piezoelectric smart structures with PID algorithm[J]. Journal of Northwestern Polytechnical University, 2017, 35(1): 74–81 [Article] (in Chinese) [Google Scholar]

[14] LI WeiguangYANG ZhichunZHU Ximing, et al. Piezoelectric adaptive active vibration suppression for wind-tunnel model support sting[J]. Smart Materials and Structures, 2024, 33(8): 085020 [Article] [Google Scholar]

[15] LI WeiguangYANG ZhichunLI Kui, et al. Hybrid feedback PID-FxLMS algorithm for active vibration control of cantilever beam with piezoelectric stack actuator[J]. Journal of Sound and Vibration, 2021, 509: 116243 [Article] [Google Scholar]

[16] GAO Z Q, AAC A C. Scaling and bandwidth-parameterization based controller tuning[C]//Annual American Control Conference, Denver, 2003 [Google Scholar]

[17] NIU WZOU CLI B, et al. Adaptive vibration suppression of time-varying structures with enhanced fxlms algorithm[J]. Mechanical Systems and Signal Processing, 2019, 118: 93–107 [Article] [Google Scholar]

[18] LI WeiguangYANG ZhichunLIU Ke, et al. Piezoelectric active disturbance rejection control for flow-induced vibration of the wind tunnel test models[J]. Mechanical Systems and Signal Processing, 2025, 224: 112010 [Article] [Google Scholar]

[19] LI BinLI YugangYIN Xuegang, et al. The modal force rule of point piezoelectric actuator place optimization on intelligent beam and frame[J]. Chinese Space Science and Technology, 20001): 3–7 (in Chinese) [Google Scholar]

[20] LIANG Li. Study on active control of vertical tail buffet with piezoelectric actuators[D]. Xi'an: Northwestern Polytechnical University, 2016 (in Chinese) [Google Scholar]