| Issue |
JNWPU
Volume 41, Number 6, Decembre 2023
|
|
|---|---|---|
| Page(s) | 1097 - 1106 | |
| DOI | https://doi.org/10.1051/jnwpu/20234161097 | |
| Published online | 26 February 2024 | |
Reliability evaluation and optimization design method of piezoelectric actuator vibration suppression system
压电作动器振动抑制系统可靠性评估及优化设计
1
School of Automobile, Chang'an University, Xi'an 710064, China
2
Beijing Mechanical and Electrical Engineering Institute, Beijing 100074, China
3
School of Aerospace Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
Received:
24
November
2022
As an effective means of structural vibration suppression, piezoelectric actuator vibration suppression system(PAVSS) has been gradually applied in structural vibration control. However, the performance degradation or failure of piezoelectric actuator under long service life will lead to the degradation of service reliability of PAVSS, so the scheme obtained by deterministic optimization method is difficult to ensure the service reliability. Aiming at the reliability evaluation and optimal design of PAVSS in service, the failure mechanism considering of the performance degradation or failure of piezoelectric actuator is analyzed, and the reliability evaluation method based on nested sampling and weighted statistics is constructed, which solves the reliability evaluation problem of PAVSS with the characteristics of load-sharing and redundancy. A reliability-based optimization method based on master-slave parallel genetic algorithm is proposed to optimize the position and angle of the actuators. At last, the feasibility and effectiveness of the proposed method are proved by an example, which not only provides a theoretical basis for the high reliability design of PAVSS in service, but also provides a new solution for the engineering problem of structural vibration control.
摘要
作为结构振动抑制的有效手段, 压电作动器振动抑制系统在结构振动控制中逐步得到应用。但是长服役期内压电作动器的性能退化/失效会导致整个振动抑制系统的服役可靠性退化, 确定性优化方法得到的方案难以保证系统的服役可靠性。针对服役期内压电振动抑制系统的可靠性评估及优化设计问题, 分析了压电作动器性能退化和失效下振动抑制系统的失效机理, 构建了基于嵌套抽样和加权统计的振动抑制系统可靠性评估方法, 解决了具有载荷共享和冗余特征的振动抑制系统可靠性评估问题, 提出了基于主从式并行遗传算法的压电作动器可靠性布局优化方法, 实现了作动器的位置和角度优化。通过算例证明了可靠性布局优化的可行性和有效性, 为服役期内振动抑制系统的高可靠性设计提供理论基础, 也可为结构振动控制这一工程问题提供新的解决思路。
Key words: PAVSS / nested sampling / weighted statistics / genetic algorithm / reliability-based optimization
关键字 : 压电作动器振动抑制系统 / 嵌套抽样 / 加权统计 / 遗传算法 / 可靠性优化
© 2023 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
由于内外载荷的综合作用, 结构在工作中必然存在振动, 剧烈的振动可能导致结构功能丧失甚至破坏, 飞行器结构振动导致的事故更是普遍存在。
对结构振动的控制一直以来都是研究的热点[1-2], 压电振动抑制系统是结构振动抑制的有效手段,目前在许多工程领域中都已取得了成功的应用, 如飞机突风减缓与颤振主动抑制、大型空间柔性结构的振动控制等。
目前, 对于压电作动器振动抑制系统的研究主要侧重于压电作动器的布局优化。Crawley等[3]运用压电作动器对压电悬臂梁振动主动控制时, 分析得到压电作动器布置于应变模态最大处控制效果最好。Gupta等[4]对压电作动器的配置优化方法作了详细总结, 讨论了基于6个标准的压电传感器和作动器的最佳布置。近年来Zhang等[5]研究了简谐激励下考虑恒定增益速度反馈(CGVF)主动控制的压电材料拓扑优化问题。Hu等[6]研究了简谐激励下薄壳结构的压电作动器拓扑优化设计问题。胡骏等[7]系统调研了考虑可控性的压电作动器拓扑优化设计方法。朱继宏等[8]指出电极材料和基体材料的拓扑优化产生的复杂边界加大了实际生产制造的难度, 并提出面向压电智能结构精确变形的压电作动器位置与结构拓扑协同优化设计方法。压电作动器位置、角度等布局优化方面, 多将遗传算法作为优化算法, 如Zhang等[9]采用非线性整数规划遗传算法对作动器的布局进行优化设计。Biglar等[10]在圆柱壳的振动控制优化设计中, 运用遗传算法得到了压电传感器和作动器粘贴在柱壳表面的最佳位置和方位。除此之外, 粒子群优化算法, 模拟退火算法等进化算法[11]也被成功用于作动器布局优化中。
压电振动抑制系统的性能受到作动器自身特性、被抑制结构的尺寸、材料、载荷等多个因素的影响, 上述各因素的随机性又导致压电振动抑制系统服役期内的性能具有随机性, 使得设计良好的系统依然存在发生故障的风险。
压电材料是具备正负压电效应能实现机械能与电能之间相互转化的一类材料。通常在交变电场下服役, 并长期工作在多场(电场、力场、温度场等)耦合情况下, 具有疲劳失效[12-15]、电击穿[16-18]和表面脱粘[19-20]等潜在失效模式。因此, 面向不确定性的振动抑制系统可靠性评估成为了振动控制领域亟待研究的关键技术。Guo[21]指出压电振动控制系统的可靠性分析和设计既不同于传统的结构可靠性问题,也不同于一般电子系统的可靠性问题,需要开发新的一体化可靠性建模和分析设计方法。目前,压电振动控制系统的可靠性评估方法可以分为非概率可靠性方法和概率可靠性方法。非概率可靠性方法基于随机变量区间的上下限进行可靠性分析,Li等[22]指出可靠性概念是解决不确定性问题的最佳途径,其将非概率可靠性分析方法引入振动主动控制系统中,提出了一种参数不确定主动控制系统可靠性问题的近似方法。Wang等[23]考虑了材料离散、载荷传递和认知不一致等不确定性, 利用空间-状态变换和凸过程理论提出了一种新的非概率可靠性评估方法。然而上述方法难以考虑振动抑制系统可靠性随服役时间的退化过程。概率可靠性方法以变量的分布为基础进行可靠性分析, 马天兵[24]指出压电作动器性能退化及失效导致的振动主动控制系统可靠性一直是振动控制领域亟待研究的关键技术, 并运用小波包和RBF神经网络来识别系统的失效概率。王滨生[25]结合压电桁架结构的力学特点, 给出了可靠性分析的安全余量表达形式, 采用改进的一次二阶矩法和Taylor展开随机有限元法给出了安全余量可靠性指标的计算方法。但上述可靠性分析方法均未考虑压电振动抑制系统的冗余和载荷共享特性, 使得系统的可靠性评估结果过于保守。
本文从压电作动器振动抑制系统原理出发, 探讨作动器性能退化和失效导致的振动抑制系统可靠性问题, 提出了基于嵌套抽样和加权统计的可靠性评估方法, 解决了具有冗余和载荷共享特性的压电振动抑制系统的可靠性评估问题, 并提出基于主从式并行NSGA-Ⅱ的压电作动器可靠性布局优化方法。最后, 通过算例证明了可靠性布局优化能够有效保证振动抑制系统服役期间内的可靠性。
1 振动抑制系统可靠性问题
1.1 压电作动器振动抑制系统功能原理
压电作动器振动抑制系统工作原理如图 1所示。
压电振动抑制系统将压电元件安置在结构中作为传感器和作动器, 压电传感器感受到结构因振动而产生的应变, 将其转变为相应的电信号, 经过一定控制算法产生控制信号, 然后再由这一控制信号驱动压电作动器对结构施加一定的控制力, 从而达到抑制结构振动的目的,是一种机电耦合作用[26]。
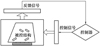 |
图1 振动抑制系统工作原理 |
1.2 压电作动器振动抑制系统失效机理分析
压电材料类型较多, 应用最广泛的是压电陶瓷(PZT), 长期在多场(电场、力场、温度场等)耦合环境下工作, 可能发生疲劳断裂、电击穿等失效模式以及出现电退化问题, 表现为作动力的下降。
在振动抑制系统中, 各压电作动器共同作用抵抗结构的振动, 即各压电作动器之间存在载荷共享特征, 这就使得一个作动器的性能退化/失效会导致其余存活作动器载荷及性能退化速率增加; 压电作动器性能退化/失效会导致结构振幅增加, 反过来加速压电作动器的性能退化/失效。因此, 二者具有耦合关系。其耦合模型如图 2所示。
由于布置位置不同, 各压电作动器的工作载荷和工作应力也不同。不考虑随机因素时, 大载荷高应力工作的压电作动器性能衰退速率较快(如A1), 小载荷低应力的压电作动器性能衰退速率较慢(如A3)。另一方面, 在抑制结构振动的过程中, 压电作动器承受交变载荷, 大载荷高应力工作的压电作动器疲劳寿命较低(如T1), 而小载荷低应力的压电作动器疲劳寿命较长(如T3)。
当有一个压电作动器(如1号)在T1时刻出现疲劳破坏时, 该作动器的输出突变到0, 振动抑制系统的抑制能力会瞬间下降, 结构振动加剧, 在闭环控制下, 剩余存活作动器(2号与3号)的工作载荷和工作应力将会提升, 并将在新的工作载荷和应力(σ′2, σ′3)下以各自新的退化速率(A′2, A′3)工作, 直到下一个作动器发生失效(如2号), 如此持续, 当抑制系统不能有效抑制结构振动时, 发生系统功能失效。
当不考虑作动器失效时间随机性时, 应力大的作动器首先失效, 因此, 各作动器的失效时间和失效顺序是确定的(即图中的1号先失效, 2号次之, 3号最后失效), 可以根据作动器的性能退化规律以及振动抑制系统的性能计算模型评估各时刻系统的振动抑制效果。
但由于随机因素的存在, 各作动器的失效时间存在分散性(即图中的T1, T2, T3存在分散性), 就可能出现载荷小的作动器先于载荷大的作动器失效(如2号先于1号发生失效), 即作动器的失效顺序具有随机性。不同失效顺序也会导致存活作动器性能退化规律以及后续失效顺序的变化, 因此, 服役期内的抑制性能具有随机性。
 |
图2 压电作动器失效与性能退化耦合模型示意图 |
1.3 压电作动器振动抑制系统可靠性模型
假设某结构在频率为x的正弦激励下的振幅为A0, 额定工作寿命为[T], 振幅阈值为[A]。振动抑制系统由m个作动器组成, 作动器最大输出载荷为Fmax, 根据结构特性, 各作动器的初始载荷分别为Fi(0), 工作应力为σi。则, 工作一段时间t后作动器输出载荷的退化量可以表示为工作应力与持续时间的函数
当第k个作动器在tk时刻出现失效时, tk之后的任意时刻, 存活作动器的实际输出载荷为
用结构的振幅表征振动抑制系统的性能, 当结构和激励确定时, 振幅是各压电作动器输出载荷的函数, 即
因此, 振动抑制系统的可靠性可以表示为
根据A(t)的单调递增特性, (4)式可以简化为
2 可靠性评估方法
2.1 压电作动器振动抑制系统可靠性评估原理
为了尽可能保证振动抑制系统的性能, 采用冗余设计, 即希望部分压电作动器失效后在其余存活作动器的共同作用下系统仍能正常工作。因此, 多压电作动器振动抑制系统是作动器冗余数量不定的载荷共享系统。一方面多个压电作动器共同作用抑制系统振动, 具有载荷共享特点, 另一方面, 压电作动器数量存在冗余, 但具体的冗余数量受到失效顺序和性能退化规律的影响。
由图 2中作动器失效与性能退化的耦合关系模型看出, 各作动器的寿命具有随机性, 而该随机性会对存活作动器后续的性能退化速率及剩余寿命产生影响, 因此, 需要在压电作动器振动抑制系统服役过程中逐个确定失效顺序及后续性能退化, 故采用嵌套抽样方法进行可靠性建模。
通过嵌套抽样的方法, 将失效顺序的不确定性问题转换为确定性问题, 在此基础上, 通过各样本的嵌套过程分析, 可获取作动器退化/失效离散性导致的系统抑制性能不确定性特征。同时, 采用加权统计方法, 可以有效解决可靠度收敛问题和嵌套抽样带来的计算效率问题。具体原理如图 3所示。
1) 在确定的作动器布局下, 基于作动器载荷分配模型, 确定各压电作动器的载荷, 进而计算作动器的寿命均值及性能退化速率。
2) 通过变异系数定义作动器的寿命分布, 并通过抽样确定哪个作动器先失效及其实际失效时间。
3) 基于失效作动器的历史失效时间确定系统的累积工作时间及存活作动器个数, 进行收敛判断。
4) 若累积工作时间达到寿命要求T或全部作动器失效, 则进入下一步。否则, 迭代执行步骤1)~3)。
5) 根据作动器的历史失效时间及失效顺序, 计算存活作动器的剩余性能及当前的系统抑制性能, 并统计上述嵌套抽样的层数。
6) 结合失效判据, 辨识各层失效样本数, 并基于失效样本的嵌套层次确定其权重, 在此基础上加权统计失效样本个数。
7) 基于样本最大嵌套层数计算样本总数并结合失效样本的加权统计结果求解系统的可靠度。
 |
图3 作动器失效和性能退化下振动抑制系统不确定性模型 |
2.2 基于加权统计的振动抑制系统可靠性评估方法
通过上述嵌套抽样可得到振动抑制系统的多个样本(同一布局下可能的多种退化过程), 下面将以含4个压电作动器的振动抑制系统为例阐述加权统计的原因和过程。
由图 4看出, 对于一个确定的布局方案, 首先进行第一轮抽样, 获取n个样本, 每个样本中包含了各压电作动器的失效时间, 从中选定寿命最短的作动器作为下一失效作动器。如果系统的历史工作时间已经超过振动抑制系统服役时间要求, 则停止对该样本的嵌套抽样, 否则, 为了得到服役时间截止时刻的振动抑制系统性能, 还需要进行下一轮抽样, 再次确定各剩余作动器中的最先失效作动器, 以此类推, 可以获取多个样本, 每一个样本的输出为服役结束时刻的振动抑制系统性能。
在上述嵌套抽样中, 得到了多个样本在服役结束时刻的振动抑制系统性能, 这些样本可能属于任一轮抽样, 在传统的统计方法中, 直接统计其中失效样本的数量和样本总量后计算失效概率, 即
很显然, 对于提前结束抽样的样本(如样本2), 如果类似于正常抽样的样本(如样本1)继续抽样, 其后续样本均为可靠样本, 抽样到最后一轮时, 样本2将演变为nm-1个可靠样本。可见, (6)式忽略了各轮样本的权重问题。
从上述分析看出, 第一轮抽样得到的可靠样本的权重较大, 最后一轮得到的可靠样本的权重较小, 因此, 当每次抽样的数量均为n时, 可得到表 1所示的样本权重。
嵌套抽样权重系数
根据表 1中的权重, 当量失效样本数为
当量样本总数为
因此, 该确定布局下压电振动抑制系统的服役可靠性为
可以看出, 模型的计算精度和效率依赖于样本量N, N由每次抽样的数据n决定。n过小会导致计算精度不足, n过大会导致计算效率过低, 因此, 在实际中需要通过尝试给出n的合理取值。
 |
图4 基于嵌套抽样的振动抑制系统可靠性模型 |
3 振动抑制系统可靠性优化设计方法
3.1 基于遗传算法的可靠性并行优化方法
振动抑制的效果不仅取决于压电作动器的性能和控制方法, 还与作动器布局方案密切相关。压电作动器的布局是影响控制系统可靠性的一个重要决定因素, 因此, 需要对作动器开展布局优化, 使得振动抑制系统在整个服役期内均具有较高的可靠性。优化流程如图 5所示。
1) 设计变量: 为了获得工程可用的作动器布局优化方案, 以作动器位置及角度作为设计变量。由于设计变量灵敏度信息获取困难, 且有很多局部最优解陷阱, 因此采用遗传算法进行优化设计。
2) 目标函数: 以系统可靠度最高为目标函数, 优化过程中可靠度计算与遗传算法的选用导致计算量过大, 采用并行策略与代理模型策略以提高优化效率。
3) 约束条件: 优化过程中压电作动器之间会产生几何干涉, 因此必须将压电作动器限制在结构空间包络边界内, 同时, 避免压电作动器相互干涉。
4) 优化算法: 采用基于代理模型的主从式并行遗传算法。一方面, 在振动抑制系统可靠性模型的基础上, 构建代理模型并进行精度验证, 利用有限的抽样点来构造代理模型以近似拟合并替代真实的功能函数, 从而降低可靠性分析中的仿真计算量。另一方面, 采用主从并行式遗传算法。该算法系统分为一个主处理器和若干从处理器: 主处理器监控整个染色体种群, 并基于全局统计执行选择、交叉和变异操作; 各个从处理器接收来自主处理器的个体并进行适应度计算, 再把结果传给主处理器。
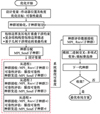 |
图5 压电作动器振动抑制系统可靠性优化流程 |
3.2 包络边界及压电作动器重叠约束检测方法
压电作动器的布局优化要求各压电作动器位于被抑制结构表面以内, 且压电作动器两两之间不相互干涉或重叠,如图 6所示。
如图 7a)所示, 以往通常将压电作动器等效为以其对角线为直径的圆形, 通过检测圆形与结构表面的相对位置来保证压电作动器位于结构表面以内, 通过检测2个作动器中心点之间的距离来保证作动器两两之间不发生干涉。
上述方法虽简单易行, 但很显然, 对于较细长的压电作动器而言, 该方法会排除过多的可行解。
通常情况下结构尺寸远远大于作动器尺寸, 而作动器形状为标准矩形, 所以通过遍历并判断压电作动器角点是否全部位于结构内部, 并结合几何学与向量计算实现判断。
由于作动器尺寸相当, 一方面需要遍历判断作动器角点是否落入其他作动器之内; 另一方面需要排除2个作动器出现如图 7b)所示的相交情况。由于压电作动器4条边都是直线段, 可以用向量叉积枚举4×4共16组对边(线段)是否相交, 向量交叉乘法方程为
如果结果小于0, 则表示向量b位于向量a的顺时针方向; 如果结果大于0, 则表示向量b位于向量a的逆时针方向; 如果等于0, 则表示向量a与向量b平行。
因此, 如果线段CD的2个端点C和D以及与另一线段(A或B, 仅其中一个)的一个端点相连的向量与向量AB交叉相乘, 如果结果不同, 则表示C和D分别位于直线AB的两侧。如果结果相同, 则表示CD的2个点位于AB的一侧, 它们不相交。
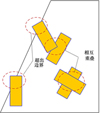 |
图6 压电作动器违反约束示意图 |
 |
图7 作动器干涉约束检测方法 |
4 算例及结果讨论
4.1 被控结构几何及边界描述
以某梯形结构为被控对象, 其几何形状如图 8所示, 其中梯形结构厚度2 mm, 材料为Al7150, 密度2 820 kg/m3, 弹性模量72 GPa, 泊松比0.35;固定支座材料为45号钢, 密度7 850 kg/m3, 弹性模量206 GPa, 泊松比0.3;支座处激励频率20 Hz; 要求持续工作时间大于30 min, 右上角处特征点振幅小于2 mm。压电材料密度7 500 kg/m3, 尺寸为50 mm×25 mm, 额定电压300 V。其余参数如表 2所示。
压电作动器材料参数
根据调研, 材料疲劳的S-N曲线一般可用幂函数、指数函数或三参数式方式表示, 本文选用了较为常用的幂函数形式[27]。本案例中假设压电作动器的S-N曲线(见图 9)和性能退化服从(11)式所示关系, 以此为基础完成可靠性设计。
实际中, 不同类型压电作动器的疲劳特性及性能退化规律存在较大差异, 可通过基础试验获取。
 |
图8 被控结构几何及边界示意图 |
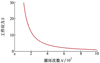 |
图9 压电作动器S-N曲线 |
4.2 作动器布局优化及可靠性评估
分别对该振动抑制系统进行确定性优化设计和可靠性优化设计, 得到布局方案及振动特性分别如图 10~11所示。其中图 10a)为初始布局,将4片压电作动器平行等间距布置于靠近翼根部位;图 10b)为基于确定性优化方法,以振幅最小为目标得到的布局方案;图 10c)为以服役期内的可靠性最高为优化目标得到的布局方案。
可以看出, 无压电控制时结构最大振幅达到8 mm, 初始布局振幅达到2 mm, 确定性优化布局振幅达到0.2 mm, 可靠性优化布局振幅达到0.5 mm。显然, 从服役初始时刻看, 确定性优化布局能获得更好的振动抑制效果, 可靠性优化布局次之, 无振动控制下效果最差。
在确定性优化布局下, 考虑作动器的失效及性能退化, 得到该布局振动抑制系统的失效概率随服役时间的演化规律, 并与可靠性优化布局振动抑制系统的失效概率演化规律对比, 得到结果如图 12所示。可见, 确定性优化得到的布局方案在服役初期失效概率很低, 但在12 min左右开始失效概率有所增加, 到服役后期失效概率增加较快, 导致在规定的最大服役时刻30 min时失效概率达到55%。相比较而言, 可靠性优化布局方案在30 min时失效概率仅为10%。
综上可以看出, 确定性优化布局下, 振动抑制系统在服役初期具有较低的失效概率, 但随着服役时间的增加, 振动抑制系统的可靠性难以保证。这是由于在确定性优化时, 不考虑使用过程中压电作动器的性能退化或失效, 通常将压电作动器布置在受载最大位置, 虽然可以使系统振动抑制能力最强, 但是后续压电作动器性能退化更快,也更容易失效, 导致长时间服役后系统失效概率迅速上升。而在规定的服役时间范围内, 可靠性优化布局已经将系统性能与可靠性综合考虑, 设计时就考虑了能够保证振动抑制系统在整个服役周期内均具有较低的失效概率, 振动抑制效果远优于确定性布局优化结果。
 |
图10 不同方法振动抑制作动器布局对比 |
 |
图11 不同布局方案服役初期振动抑制效果对比 |
 |
图12 不同布局方案系统失效概率演化规律对比 |
5 结论
针对工程中的振动抑制需要, 研究了压电振动抑制系统的可靠性模型, 采用嵌套抽样和加权统计方法提出了具有冗余和载荷共享特性的压电振动抑制系统的可靠性评估方法, 并提出基于主从式并行遗传算法的压电作动器可靠性布局优化方法。根据模型和结果可以得到如下结论:
1) 压电作动器振动抑制系统具有冗余和载荷共享特性, 压电作动器的性能退化/失效与振动抑制系统性能相互影响, 具有耦合关系。
2) 嵌套抽样方法能很好地描述压电作动器振动抑制系统的失效过程和行为, 可以有效解决系统可靠性评估问题。
3) 改进作动器干涉检测方法并采用并行遗传算法后的可靠性布局优化能够在保证系统性能的同时降低压电作动器的性能退化速率, 使得服役期间可靠性得到保障。
4) 结果表明采用可靠性布局优化后, 案例所示的压电作动器振动抑制系统的服役过程的失效概率可以由0.56降至0.11, 可靠性大幅提高。
References
- YANG Jiajia, HE Erming, SHU Juncheng. Application of adaptive fuzzy control to suppression vibration response of floating offshore wind turbine[J]. Journal of Northwestern Polytechnical University, 2021, 39(2): 241–248 [Article] (in Chinese) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ZHANG Shuyang, ZHANG Shunqi, LI Jing, et al. Shape control and active vibration control of piezoelectric smart structures with PID algorithm[J]. Journal of Northwestern Polytechnical University, 2017, 35(1): 74–81 [Article] (in Chinese) [Google Scholar]
- CRAWLEY E F, LUIS J. Use of piezoelectric acuators as elements of intelligent structures[J]. AIAA Journal, 1987, 25(10): 1373–1385 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- GUPTA V, SHARMA M, THAKUR N. Optimization criteria for optimal placement of piezoelectric sensors and actuators on a smart structure: a technical review[J]. Journal of Intelligent Material Systems and Structures, 2010, 21(12): 1227–1243 [Article] [CrossRef] [Google Scholar]
- ZHANG X, KANG Z, LI M. Topology optimization of electrode coverage of piezoelectric thin-walled structures with CGVF control for minimizing sound radiation[J]. Structural and Multidisciplinary Optimization, 2014, 50(5): 799–814 [Article] [CrossRef] [Google Scholar]
- HU K, LI H. Multi-parameter optimization of piezoelectric actuators for multi-mode active vibration control of cylindrical shells[J]. Journal of Sound and Vibration, 2018, 426: 166–185 [Article] [CrossRef] [Google Scholar]
- HU Jun, KANG Zhan. [Topology optimization of piezoelectric actuator considering controllability[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(4): 1073–1081 (in Chinese) [Google Scholar]
- WU Manqiao, ZHU Jihong, YANG Kaike, et al. Integrated layout and topology optimization design of piezoelectric smart structure in accurate shape control[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(2): 380–389 (in Chinese) [Google Scholar]
- ZHANG C, WANG L, WU X, et al. A novel optimal configuration of sensor and actuator using a non-linear integer programming genetic algorithm for active vibration control[J]. Journal of Intelligent Material Systems and Structures, 2017, 28(15): 2074–2081 [Article] [CrossRef] [Google Scholar]
- BIGLAR M, MIRDAMADI H R, DANESH M. Optimal locations and orientations of piezoelectric transducers on cylindrical shell based on gramians of contributed and undesired Rayleigh-Ritz modes using genetic algorithm[J]. Journal of Sound and Vibration, 2014, 333(5): 1224–1244 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- HUANG Xiufeng, CUI Hongyu, HONG Ming, et al. Advances in optimal allocation of piezoelectric sensor actuator in structural vibration control[J]. Piezoelectrics & Acoustooptics, 2015, 37(5): 768–779 (in Chinese) [Google Scholar]
- XIE Li, WANG Jiaqiu, ZHONG Zheqiang, et al. Influence of fatigue of piezoelectric ceramic actuators on correction bandwidth of deformable mirrors[J]. Acta Photonica Sinica, 2019, 48(9): 0912005 (in Chinese) [CrossRef] [Google Scholar]
- LEI J, WANG H, ZHANG C, et al. Comparison of several BEM-based approaches in evaluating crack-tip field intensity factors in piezoelectric materials[J]. International Journal of Fracture, 2014, 189: 111–120 [Article] [CrossRef] [Google Scholar]
- LEI J, ZHANG C. A simplified evaluation of the mechanical energy release rate of kinked cracks in piezoelectric materials using the boundary element method[J]. Engineering Fracture Mechanics, 2018, 188: 36–57 [Article] [CrossRef] [Google Scholar]
- MISHRA R K. A review on fracture mechanics in piezoelectric structures[J]. Materials Today: Proceedings, 2018, 5: 5407–5413 [Article] [CrossRef] [Google Scholar]
- MARTÍNEZ-AYUSO G, FRISWELL M I, KHODAPARAST H H, et al. Electric field distribution in porous piezoelectric materials during polarization[J]. Acta Materialia, 2019, 173: 332–341 [Article] [CrossRef] [Google Scholar]
- ZHENG D, LUO M, SWINGLER J. Multi-breakdown model for explaining the formation and growth of black spots in PZT capacitor under DC bias[J]. Sensors and Actuators A: Physical, 2016, 241: 197–202 [Article] [CrossRef] [Google Scholar]
- LOBODA V, SHEVELEVA A, Chapellec F. A dielectric breakdown model for an electrode along an interface between two piezoelectric materials[J]. Engineering Fracture Mechanics, 2020, 224: 106809 [Article] [CrossRef] [Google Scholar]
- CHEN P J, PENG J, LIU H, et al. The electromechanical behavior of a piezoelectric actuator bonded to a graded substrate including an adhesive layer[J]. Mechanics of Materials, 2018, 123: 77–87 [Article] [CrossRef] [Google Scholar]
- KHAN A, Kim H S, Youn B D. Modeling and assessment of partially debonded piezoelectric sensor in smart composite laminates[J]. International Journal of Mechanical Sciences, 2017, 132: 26–37 [CrossRef] [Google Scholar]
- GUO S X. An efficient third-moment saddlepoint approximation for probabilistic uncertainty analysis and reliability evaluation of structures[J]. Applied Mathematical Modelling, 2014, 38: 221–232 [Article] [CrossRef] [Google Scholar]
- LI Y L, WANG X J, WANG L. Non-probabilistic stability reliability measure for active vibration control system with interval parameters[J]. Journal of Sound and Vibration, 2017, 387: 1–15 [Article] [CrossRef] [Google Scholar]
- WANG L, WANG X J, WU D. Non-probabilistic time-variant reliability assessment (NTRA) for the active control of vibration systems with convex uncertainties[J]. ISA Transactions, 2018, 83: 276–289 [Article] [CrossRef] [Google Scholar]
- MA Tianbing. Research on key technologies of active vibration control for piezoelectric smart structures[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014 (in Chinese) [Google Scholar]
- WANG Binsheng. System reliability analysis of piezoelectric truss structures[D]. Harbin: Harbin Engineering Uiversity, 2008 (in Chinese) [Google Scholar]
- WANG Xiong, GAO Yingshan, ZHANG Shunqi, et al. Electromechanical coupling modeling and analysis of piezoelectric damping laminated structures based on zig-zag hypothesis[J]. Journal of Northwestern Polytechnical University, 2022, 40(2): 407–413 [Article] (in Chinese) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ZHANG Yajun. Discussion on processing method for mathematical expression of S-N fatigue curve[J]. Physical Testing and Chemical Analysis(Part A: Physical Testing), 2007(11): 563–565 [Article] (in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 振动抑制系统工作原理 |
| In the text | |
 |
图2 压电作动器失效与性能退化耦合模型示意图 |
| In the text | |
 |
图3 作动器失效和性能退化下振动抑制系统不确定性模型 |
| In the text | |
 |
图4 基于嵌套抽样的振动抑制系统可靠性模型 |
| In the text | |
 |
图5 压电作动器振动抑制系统可靠性优化流程 |
| In the text | |
 |
图6 压电作动器违反约束示意图 |
| In the text | |
 |
图7 作动器干涉约束检测方法 |
| In the text | |
 |
图8 被控结构几何及边界示意图 |
| In the text | |
 |
图9 压电作动器S-N曲线 |
| In the text | |
 |
图10 不同方法振动抑制作动器布局对比 |
| In the text | |
 |
图11 不同布局方案服役初期振动抑制效果对比 |
| In the text | |
 |
图12 不同布局方案系统失效概率演化规律对比 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


