EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 1 (February 2025) JNWPU, 43 1 (2025) 31-39 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 1, February 2025
Page(s) 31 - 39
DOI https://doi.org/10.1051/jnwpu/20254310031
Published online 18 April 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

船舶在极地等气候寒冷恶劣的海上环境下航行时, 上层结构经常会遭遇结冰问题, 严重时会导致船舶失稳, 对结构体和部件造成超载从而产生破坏, 并对室外环境作业安全构成威胁[1–2]。含盐海水飞沫结冰是导致上层结构结冰的主要原因, 飞沫从低水温的海面产生, 进入更低温度的空气, 最后撞击壁面并发生结冰。研究含盐飞沫结冰的相关试验较为复杂, 结冰环境及工况难以实现精确控制, 且其中的盐分会侵蚀相关试验设备, 因此开展数值模拟成为了研究含盐飞沫结冰的重要手段。对于结冰问题, 通常将海水飞沫简化为含盐的液态水滴, 即含盐水滴(本文中简称为液滴)[3–4]。

针对颗粒的撞击特性以及含盐水滴的结冰相变过程, 国内外研究者开展了一系列研究。马乙楗等[5]基于蒙特卡洛方法实现了颗粒撞击特性计算, 克服了粒子运动轨迹交叉问题。胡良权等[6]针对风力机叶片结冰问题, 采用欧拉两相流模型计算了NACA64618叶片的水滴收集系数。Lozowski等[7]指出可以在计算模型中以盐度为0.1‰的盐水模拟淡水冰的增加, 来解决盐水和淡水的海绵冰算法不匹配问题。Horjen[8]在ICEMOD系列模型中对不同直径的圆柱体进行了含盐水滴结冰计算。Kulyakhtin等[9–10]开发了应用CFD技术的MARICE模型, 结合了Myers和Charpin[11]开发的改进淡水冻结模型, 并通过添加盐度守恒方程来加强该模型。白旭等[12]使用相场法研究海水盐度对冰晶生长的影响, 并分析了不同盐度下结冰的微观结构特性。刘宇等[13]通过建立相似准则, 使用纯水结冰模拟含盐飞沫结冰。结冰模型的发展, 大多聚焦于某个阶段应用新技术或新方法, 来提高结冰计算精度[14]。

目前国内外现有针对海水飞沫的结冰计算模型, 在飞沫运动过程中仅考虑了蒸发对传热的影响, 但忽略了蒸发导致的质量损失和盐度变化[15]。对于大粒径飞沫液滴, 蒸发引起的质量下降通常可以忽略不计, 但对于小粒径飞沫液滴, 蒸发会导致液滴质量明显下降, 对于撞击特性的计算及结冰相变计算均会有一定影响。

由于液滴在运动过程中存在传热传质效应, 不同粒径液滴的质量及盐度会出现不同程度的改变, 从而会对撞击特性的计算及结冰相变计算产生不同程度影响。本文基于国内自主开发的NNW-ICE结冰平台, 结合含盐水滴的运动-传热传质耦合模型, 采用蒙特卡洛方法实现了含盐水滴撞击特性计算[16], 为其结冰相变计算提供更加准确的参数输入; 并结合ICEMOD、MARICE、SHIPICE[17]3种模型中飞沫结冰相变阶段部分工作, 基于NNW-ICE平台开发了含盐水滴结冰相变计算代码, 从而形成了完备的结冰相变数值计算程序, 并为模型的进一步发展奠定了基础。

1 计算方法

基于NNW-ICE平台建立了拉格朗日框架下含盐水滴收集系数计算方法, 并结合了含盐水滴运动相变实现了更加符合物理实际的液滴撞击质量通量计算, 同时考虑了蒸发带走的热量和质量。在此基础上开发了针对含盐水滴的结冰相变计算方法。建模及计算过程基于以下假设[17–19]: ①水膜层上的温度和盐混合均匀; ②忽略水膜中的温度梯度; ③忽略液滴的气动热量和动能; ④忽略冰层孔隙中未冻结水的结冰; ⑤忽略已形成冰层中的导热传热。

1.1 含盐水滴运动-传热传质模型及蒙特卡洛方法

1.1.1 运动控制方程及阻力模型

液滴运动主要由空气阻力和重力控制, 基于液滴的球形假设并忽略运动过程中的聚集和破碎, 在Lagrange框架下, 液滴运动控制方程为[15]

式中: up为液滴速度; ua为来流速度(风速); Cd为阻力系数; dp为液滴直径; ρa为空气密度, ρp为液滴密度; g为重力加速度。

Hoes[17]在SHIPICE模型中使用的阻力系数计算式(本文中简称Hoes)

式中, Re为雷诺数。

Lozowski等[7]使用的Langmuir等[20]给出的阻力系数计算式(本文中简称Lang)

Dehghani等[21]使用的阻力系数计算式(本文中简称Dehg)

1.1.2 含盐水滴传热传质耦合模型

由于运动过程中与气流的对流、蒸发和辐射换热, 液滴会冷却降温。液滴冷却方程由对流热通量、蒸发热通量和长波辐射热通量控制。含盐水滴冷却方程为[15]

式中: mp为液滴质量; cp为液滴比热容; Tp为液滴温度; C为对流热通量; R为长波辐射热通量; 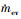为蒸发质量速率; Lv为液滴温度下的蒸发比潜热。

含盐水滴蒸发导致质量的变化导致其盐度变化, 进一步导致冻结温度发生变化, 液滴在运动传质过程中含盐质量不变, 当地位置的液滴盐度为

式中：S为当前位置液滴的盐度；ms为液滴含盐质量；mp, start为液滴初始质量；Sstart为液滴初始盐度。

1.1.3 蒙特卡洛收集系数计算方法

基于蒙特卡洛方法(Monte Carlo method)的局部收集系数βSME, MC的表达式为[5, 18]

式中：MSME为表面网格单元SME(surface mesh element)从τ0到τtotal时刻的质量流率积分；τ0为计算初始时刻；τtotal为计算结束时刻, CLW为空气中的液态水含量(liquid water content)；v∞为来流远场速度；ASME为SME的面积。

含盐水滴撞击质量通量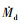的表达式为

1.2 含盐水滴结冰相变模型

1.2.1 含盐水滴结冰相变控制方程

对于连续撞击液滴的结冰相变过程, 主要热通量由对流热通量Qc、蒸发热通量Qe、辐射热通量Qr、撞击热容Qd组成。其结冰相变控制方程为[11]

式中：ρi为积冰密度；Lf为冰的熔化潜热；b为积冰厚度；σ为界面分布系数(困在冰中的未冻结液态水密度)。

对流热通量Qc表示为

式中：hc为液滴对流换热系数；Tw为水膜温度；Ta为空气温度；Nu为液滴的努塞尔数；ka为气流热导率; c为组件特征长度。

蒸发热通量Qe表示为

式中：Pr为普朗特数；Sc为施密特数；ε为液滴与空气的摩尔质量比；Le为蒸发潜热；p为大气压；ca为空气的比热容；HR为相对湿度(relative humidity)；es(T)为温度T下的饱和液滴压力。

撞击热容Qd表示为

式中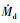：为撞击质量通量；cw为液滴比热容；Td为撞击液滴温度。

辐射热通量Qr表示为

1.2.2 冻结温度模型

液滴的盐度与该盐度下的冻结温度存在一定关系, 该关系在本文中以冻结温度模型表示。MARICE模型[9]中采用的冻结温度模型为

ICEMOD模型中采用的冻结温度模型为

式中，Tf为盐度S下冻结温度; 常数α0=-3.992 1, α1=-22.7, α2=-1.001 5, α3=-0.019 956。

1.3 计算求解流程

根据1.1节给出的含盐水滴撞击质量通量计算方法, 和1.2节给出的含盐水滴结冰相变控制方程, 提出含盐水滴完整数值计算方法流程如图 1所示。

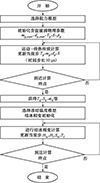thumbnail 图1

完整数值计算流程

1) 选择阻力系数模型, 进行液滴运动-传热传质耦合计算, 获取上下撞击极限、质量损失率、撞击液滴温度Td、撞击液滴盐度Sd等数据;

2) 使用蒙特卡洛方法计算收集系数βSME, MC及撞击质量通量;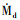

3) 选择冻结温度模型, 将运动模块的计算数据作为结冰相变模块的输入参数;

4) 进行含盐水滴结冰相变计算, 输出水膜盐度、积冰质量、结冰强度等数据。

2 含盐水滴撞击特性计算及验证

不考虑运动相变时, 含盐液滴与纯水水滴撞击特性的计算方法一致。为验证程序撞击特性计算的有效性, 参照文献[22]设置工况, 选择弦长0.91 m的NACA23012翼型为撞击壁面, 进行含盐水滴收集系数计算验证。图 2给出了在来流温度Ta=299 K、来流速度ua=78.23 m/s的工况下, 忽略运动相变的20 μm纯水水滴以2.5°攻角撞击NACA23012翼型前缘的计算结果对比。

thumbnail 图2

NACA23012翼型撞击收集系数对比

由图 2可知, 对于NACA23012翼型表面撞击收集系数, NNW-ICE计算结果与文献计算结果中的撞击极限吻合较好, 撞击下极限在弧长比弦长s/L为-0.05处, 撞击上极限在s/L为0.037处; NNW-ICE与文献中收集系数峰值计算结果非常接近分别为0.606和0.599, 均大于试验结果的0.559, 与试验结果的相对误差分别为8.401%和7.156%。NNW-ICE计算结果与文献[22]试验结果的整体趋势符合度更好, 收集系数峰值出现的位置更加接近, 能够验证NNW-ICE收集系数计算程序的有效性。

为了探究不同阻力系数模型对于含盐水滴收集系数计算的影响, 基于上述工况, 在3种阻力模型下进行了含盐水滴撞击收集系数计算, 结果如图 3所示。由图可知, 撞击极限及收集系数均是Hoes较大, Dehg次之, Lang相对较小; 收集系数峰值分别为0.631, 0.618, 0.606, Hoes与Lang计算结果相差为4.125%。计算结果表明不同的阻力系数模型下计算的撞击极限和收集系数相差不大, Hoes阻力模型下的计算结果相对更大, Lang阻力模型下的计算结果相对较小。

thumbnail 图3

不同阻力系数模型下的收集系数计算

由于含盐水滴运动过程伴随着质量损失, 运动传质效应可能对其撞击特性的计算有一定的影响, 为了探究液滴运动相变对于撞击特性计算的影响, 参考文献[15]进行计算工况设置: 来流相对湿度HR=70%, 来流温度Ta=258.15 K, 液滴初始温度Tw=272.15 K, 来流速度ua = 10 m/s, LWC为1 g/m3, 运动距离10 m, 采用Hoes阻力系数模型, 设置0°攻角, 选择NACA0012翼型撞击壁面, 选取盐度为35‰的20, 30, 83, 260 μm 4种粒径液滴进行计算。表 1给出了考虑运动相变的不同粒径液滴在壁面驻点处的撞击液滴温度Td、撞击液滴盐度Sd、质量保存率mp/mp, start(当前位置的质量比初始质量)、撞击质量通量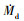的计算数据, 以及开启相变后的撞击质量通量相较于开启运动相变前计算结果的下降幅度; 撞击壁面质量通量的计算结果如图 4所示。

表1

驻点处含盐水滴结冰关键物理量结果

thumbnail 图4

不同粒径液滴撞击质量通量计算

由图 4和表 1可知, 较小粒径液滴由于传热传质效应更加显著, 开启运动相变后, 20, 30 μm粒径液滴的撞击质量通量的计算结果下降幅度较大, 分别为23.97%, 10.67%。开启运动相变后由于小粒径液滴质量损失百分比较大, 导致其撞击质量通量计算结果显著减小; 83, 260 μm粒径液滴撞击质量通量降低幅度在3%以内, 可以忽略, 这是因为较大粒径液滴对于运动传质效应不敏感, 撞击特性计算受到的影响非常有限; 另外, 由于较大粒径液滴受重力作用明显, 导致撞击极限不对称。

3 含盐水滴结冰相变计算及验证

为验证程序结冰相变计算的有效性, 参照文献[17]设置计算工况, 选择二维圆柱为撞击壁面, 来流及云雾边界条件设置如表 2所示。采用1.2.2节描述的2种冻结温度模型, 基于NNW-ICE平台进行数值验证, 选择撞击区域中迎风驻点单元, 计算单位面积的含盐水滴周期性撞击的结冰强度(icing intensity)、水膜盐度(brine film salinity)及积冰质量(accreted icing mass), 并与文献[17]中SHIPICE模型及ICEMOD模型的计算结果进行对比, 结果分别如图 5~7所示。其中, 结冰强度表征单位时间内单位面积的结冰质量。

表2

对比验证算例工况

thumbnail 图5

结冰强度计算对比[17]

thumbnail 图6

水膜盐度对比[17]

thumbnail 图7

积冰质量对比[17]

图 5展示了结冰强度的计算结果; 图 6展示的是水膜盐度变化曲线; 图 7展示了单位面积的积冰质量增长曲线。在上述各图中NNW-ICE计算结果与ICEMOD、SHIPICE中计算结果曲线变化趋势一致且吻合较好。在首次连续撞击过程中结冰强度呈直线状态, 且水膜盐度变化可以忽略, NNW-ICE与SHIPICE在-8 ℃下结冰强度为1.05, 1.09 g/m2/s, 水膜盐度分别为37.5‰, 37.9‰, ICEMOD结冰强度约为1.06 g/m2/s, 水膜盐度为37.8‰。在-12 ℃工况下NNW-ICE、SHIPICE与ICEMOD连续撞击结冰强度分别为1.89, 1.91, 1.94 g/m2/s, 水膜盐度分别为40.8‰, 41.7‰, 41.5‰。结冰强度的值在每一次连续撞击结束时会出现突变上升的情况, 之后由于没有新的液滴进入水膜, 随着结冰相变的进行盐度逐渐排入剩余水膜导致盐度增大, 冻结温度降低, 结冰强度减小且其降低程度逐步增大。直到下一周期液滴开始撞击壁面, 由于新的液滴加入水膜, 水膜厚度变大, 盐度降低, 结冰强度再次出现突变上升而后逐步增长, 随着时间增速逐渐变缓。在-8 ℃工况下, NNW-ICE计算的水膜盐度曲线与文献中计算结果均吻合较好, 随着结冰过程的进行, 水膜盐度变化幅度逐渐变小, NNW-ICE、SHIPICE与ICEMOD最终计算得到的单位面积积冰质量分别为102.0, 104.9, 102.9 g/m2。对于-12 ℃计算工况, 除了最初的连续撞击结冰过程, SHIPICE中的水膜盐度在整个周期性变化过程中数值总是更小, NNW-ICE与ICEMOD的计算结果更加接近, 这是由于采用冻结温度模型不同导致的, 不同冻结温度模型在同一温度下对应不同数值的盐度, 在部分工况下对水膜盐度变化曲线的影响较明显, 但对于结冰强度及积冰质量计算影响很小。-12 ℃工况下, 结冰83 s后NNW-ICE、SHIPICE与ICEMOD单位面积积冰质量分别为152.2, 154.4, 150.1 g/m2, 差距不大。表 3~4分别给出了-8, -12 ℃下10个周期内NNW-ICE、SHIPICE与ICEMOD的计算数据对比及NNW-ICE相较于ICEMOD的误差。

表3

Ta=-8 ℃计算结果及误差

表4

Ta=-12℃计算结果及误差

以上结果已经证明了NNW-ICE对于含盐水滴结冰相变过程中的结冰强度、水膜盐度以及积冰质量计算的可靠性。NNW-ICE与ICEMOD模型进行了更多的计算验证, 改变表 3中部分参数, 在-10 ℃空气温度下, 计算连续液滴撞击及频率N减半(即周期Ts加倍)工况下驻点的结冰强度, 与ICEMOD结果对比如图 8所示, 表 5给出了不同周期下首次连续撞击阶段的结冰强度和结冰强度最大值的计算数据及误差; 在来流速度25 m/s、空气温度-10 ℃下, 计算整个圆形表面24 h结冰厚度, 结果如图 9所示。

thumbnail 图8

不同周期撞击液滴结冰强度[8]

表5

Ta=-10 ℃结冰强度计算结果及误差

thumbnail 图9

表面冰厚[8]

图 8中, 蓝色点线周期工况为8.30 s, 绿色点线周期工况为16.60 s, 在每一个周期内, 撞击持续时间为2.56 s。在给定的计算工况下, NNW-ICE与ICEMOD在不同周期中各时间段计算的含盐水滴结冰强度变化趋势一致; 由表 5可知同一个周期内连续撞击结束时结冰强度突变后数值的相对误差保持在1%以下, 双倍周期工况下的首次连续撞击阶段结冰强度误差为8.43%, 单倍周期的首次连续撞击阶段及全程连续撞击工况下结冰强度计算的相对误差均小于2%, 误差程度均在可接受范围。

图 9中展示了在相应工况下, 基于NNW-ICE平台采用2种冻结温度模型计算得到的结冰24 h的表面冰厚结果。

NNW-ICE结冰平台采用2种模型所得的冰厚计算结果均与文献[8]结果吻合较好, 采用MARICE冻结温度模型得到的计算结果更接近该文献ICEMOD模型的计算结果, 不同冻结温度模型下滞止点(0°)处结冰厚度均接近18 cm, 整个表面最大厚度出现的角度位置均在30°附近。

根据上述分析可知, 基于NNW-ICE结冰平台所开发的计算程序得到的结冰强度等结冰参数的计算结果与文献结果趋势一致、吻合度高, 通过本章中各算例验证了NNW-ICE平台所开发的含盐水滴结冰相变计算程序的可靠性。

4 结论

本文基于NNW-ICE平台建立了在拉格朗日框架下计算含盐水滴撞击收集系数的蒙特卡洛计算方法, 结合含盐水滴运动-传热传质模型实现了其撞击特性的计算。在此基础上开发了含盐水滴结冰相变模块, 与上述模块组成了完整的含盐水滴结冰计算程序。主要得到以下结论:

1) 本文结果与文献[22]中相同工况下的液滴撞击收集系数计算结果符合较好, 表明了含盐水滴撞击特性计算程序的可靠性, NNW-ICE结冰平台采用该计算程序能够有效模拟含盐水滴的撞击质量通量计算。

2) 对比了同一工况下不同阻力系数模型以及运动相变对撞击特性计算的影响, 结果表明阻力系数模型对收集系数计算结果影响较小, 含盐水滴的运动-传热传质效应对于较小粒径液滴的撞击质量通量的计算影响较为显著。

3) 本文结果与文献[8, 17]中不同工况下撞击壁面驻点单元的结冰强度、水膜盐度、积冰质量、壁面积冰厚度计算结果符合较好, 计算结果相差均在10%以内, 表明了基于NNW-ICE平台的含盐水滴结冰相变计算程序具备较高的可靠性。

References

  1. ZHOU LLIU RYI X. Research and development of anti-icing/deicing techniques for vessels: Review[J]. Ocean Engineering, 2022, 260: 112008 [Article] [Google Scholar]
  2. ZHOU LiangLI WeihaoSHI Yanan, et al. Overview of foreign research on ship spray icing[J]. Ship Science and Technology, 2022, 44(10): 1–5 (in Chinese) [Google Scholar]
  3. HAN DuanfengWANG YongkuiJU Lei, et al. Phase field simulation of ice crystal growth in seawater freezing process[J]. Journal of Harbin Engineering University, 2020, 41(1): 1–8 (in Chinese) [Google Scholar]
  4. YANG Sujie, BAI Xu. Phase field simulation during recalescence and collision characteristics of supercooled droplets in polar ship icing[D]. Zhengjiang: Jiangsu University of Science and Technology, 2022 (in Chinese) [Google Scholar]
  5. MA YijianCHAI DelinWANG Qiang, et al. Phase change and adhesion characteristics of ice crystal movements in wing icing[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(1): 41–52 (in Chinese) [Google Scholar]
  6. HU LiangquanCHEN JingeSHEN Xin, et al. Calculation of freezing water droplet collection coefficient of wind turbine blades[J]. Acta Energiae Solaris Sinica, 2020, 41(3): 22–28 (in Chinese) [Google Scholar]
  7. LOZOWSKI E PSZILDER KMAKKONEN L. Computer simulation of marine ice accretion[J]. Mathematical, Physical and Engineering Sciences, 2000, 358(1776): 2811–2845 [Article] [Google Scholar]
  8. HORJEN I. Offshore drilling rig ice accretion modeling including a surficial brine film[J]. Cold Regions Science and Technology, 2015, 119: 84–110 [Article] [Google Scholar]
  9. KULYAKHTIN ATSARAU A. A time-dependent model of marine icing with application of computational fluid dynamics[J]. Cold Regions Science and Technology, 2014104/105): 33–44 [Google Scholar]
  10. KULYAKHTIN AKULYAKHTIN SLØSET S. The role of the ice heat conduction in the ice growth caused by periodic sea spray[J]. Cold Regions Science and Technology, 2016, 127: 93–108 [Google Scholar]
  11. MYERS T GCHARPIN J P F. A mathematical model for atmospheric ice accretion and water flow on a cold surface[J]. International Journal of Heat and Mass Transfer, 2004, 47(25): 5483–5500 [Google Scholar]
  12. BAI XuYANG SujieTIAN Yukui. Simulation analysis of the effect of salinity on the microscopic characteristics of seawater icing based on improved phase field method[J]. Journal of Ship Mechanics, 2022, 26(10): 1496–1502 (in Chinese) [Google Scholar]
  13. LIU YuQIN MengjieWANG Qiang. Study on similarity criterion for icing wind tunnel test of saline seawater droplets[J]. Journal of Aeronautics, 2023, 44(suppl.2): 729297 [Google Scholar]
  14. WANG Shijing. Research on ship ice accumulation prediction model in polar waters[D]. Dalian: Dalian University of Technology, 2018 (in Chinese) [Google Scholar]
  15. TANG YuhaoCHAI DelinMA Yijian, et al. Characteristics of heat and mass transfer in salty droplet motion and its influencing factors[J]. Acta Aeronautica et Astronautica Sinica, 2023, 42(4): 55–64 (in Chinese) [Google Scholar]
  16. LIU YQU J GYI X, et al. A Monte Carlo Lagrangian droplet solver with backpropagation neural network for aircraft icing simulation[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2023, 40(5): 566–577 [Google Scholar]
  17. HOES C M. Marine icing: a probabilistic icing model from sea generated spray[D]. Delft: Delft University of Technology, 2016 [Google Scholar]
  18. DEHGHANI-SANIJ A RDEHGHANI S RNATERER G F, et al. Marine icing phenomena on vessels and offshore structures: prediction and analysis[J]. Ocean Engineering, 2017, 143: 1–23 [Google Scholar]
  19. CHEN NYI XWANG Q, et al. An analysis of heat transfer inside the ice layer and solid wall during ice accretion[J]. International Communications in Heat and Mass Transfer, 2022, 137: 106276 [Google Scholar]
  20. LANGMUIR IBLODGETT K B. A mathematical investigation of water droplet trajectories[M]. New York: Pergamon Press, 1946 [Google Scholar]
  21. DEHGHANI S RMUZYCHKA Y SNATERER G F. Droplet trajectories of wave-impact sea spray on a marine vessel[J]. Cold Regions Science and Technology, 2016, 127: 1–9 [Google Scholar]
  22. SZNAJDER J. Implementation of an eulerian method of determination of surface water collection efficiency for atmospheric icing problems[J]. Transactions of the Institute Aviation, 2015, 238(1): 91–105 [Google Scholar]

All Tables

表1

驻点处含盐水滴结冰关键物理量结果

In the text
表2

对比验证算例工况

In the text
表3

Ta=-8 ℃计算结果及误差

In the text
表4

Ta=-12℃计算结果及误差

In the text
表5

Ta=-10 ℃结冰强度计算结果及误差

In the text

All Figures

thumbnail 图1

完整数值计算流程
In the text
thumbnail 图2

NACA23012翼型撞击收集系数对比
In the text
thumbnail 图3

不同阻力系数模型下的收集系数计算
In the text
thumbnail 图4

不同粒径液滴撞击质量通量计算
In the text
thumbnail 图5

结冰强度计算对比[17]
In the text
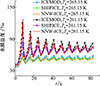thumbnail 图6

水膜盐度对比[17]
In the text
thumbnail 图7

积冰质量对比[17]
In the text
thumbnail 图8

不同周期撞击液滴结冰强度[8]
In the text
thumbnail 图9

表面冰厚[8]
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.