EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 3 (June 2025) JNWPU, 43 3 (2025) 536-545 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 3, June 2025
Page(s) 536 - 545
DOI https://doi.org/10.1051/jnwpu/20254330536
Published online 11 August 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

卫星及其载荷技术的快速发展和复杂空天应用需求的增长, 使卫星星座对地覆盖问题成为空间科技领域的研究热点[1]，提升大规模星座覆盖地球的效率与精度已成为关键挑战。

一类研究聚焦于多卫星轨迹、投影和覆盖问题, Ortore等[2]通过地面轨迹分析构建关系式以优化轨迹距离和重访频率。Dai等[3]利用投影点几何配置分解覆盖区域。Wang等[4]提出ECHO(envelope curves hierarchical overlapping)双阶段法分析敏捷卫星覆盖。闫野等[5]提出了一种简单快速的判定方法, 能够有效地判断卫星星座是否在某一时刻实现了地球的N重全球覆盖。Ulybyshev[6]通过二维映射和可见性特性分析地球表面的特定区域在不同时间间隔的覆盖性能。Gong等[7]利用星座的对称性, 计算最小单元中重复覆盖性能的卫星, 并通过卫星的相位分布解决覆盖区域的重叠。

另一类研究则侧重于改进算法与优化方法。如Zhang等[8]考虑J2摄动简化覆盖计算, Xu等[9]改进成像方法获取覆盖率关系, 吕林立等[10]优化巨型星座评估流程。Chen等[11]依据对卫星流形的综合评估, 提供了优化星座配置以实现地球覆盖的策略。Zhou等[12]将复杂的连续覆盖问题转换为分析卫星覆盖范围的关键地心角度和特征距离之间的关系。陈晓宇等[13]运用球面Delaunay三角网和Voronoi图的特性, 分析了星座的空间几何配置划分方法, 并定义了每颗卫星的覆盖区域。吴焕芹等[14]提出了一种基于椭球理论的方法用于估计卫星入轨位置的随机误差。简平等[15]通过改进网格划分规则解决了网格点仿真方法在空间覆盖特性统计分析中的不足。Hang等[16]首次引入了利用循环卷积特性优化星座的模式, 可以同时处理多个目标区域和多个子星座的分析。Chen等[17]考虑任务执行时间依赖等操作约束, 提出了基于数据驱动的双阶段多星数传协同规划方法。

其中, 网格法作为经典的区域分解方法, 主要包括等经纬度法和等面积法。等经纬度法将等经纬度划分的球面映射到二维平面上形成网格。阮启明等[18]建立了多星协同区域覆盖问题的约束优化模型, 将禁忌算法与约束传播相结合以迭代方式获得最优解。Shao等[19]利用等经纬度的网格将区域目标分解成多个点目标, 并在此基础上建立了双目标规划模型。刘华俊等[20]将实际覆盖率和计算效率表示成网格经纬度的函数, 通过最大化2个函数乘积的平方根来确定最佳网格大小的取值。宋志明等[21]将地面区域按经度分条带划分, 从而快速评估星座的地面覆盖情况。等面积法则是将目标区域划分为若干个相同面积的网格[22-24]。部分研究将网格简化为离散点集[25-26], 此类方法将计算网格面积转换为统计覆盖点数, 本质上仍属网格思想。

针对现有方法的局限, 本文提出基于Delaunay三角网和多粒度分层网格划分混合的多星对地覆盖计算方法。该方法首先利用球面Delaunay三角剖分[27]分割目标区域为球面三角形, 再结合网格法精确评估各三角形覆盖状况, 汇总后即可得目标区域的瞬时与连续覆盖率。该策略显著提升了计算效率, 并能灵活处理各类形状的地面目标。

1 星地覆盖问题形式化描述

令\begin{document}$S$\end{document}为1颗卫星。将多个卫星构成的星座记作\begin{document}$\boldsymbol{C}$\end{document}, 则星座\begin{document}$\boldsymbol{C}$\end{document}可看作1组卫星的集合, 记作

式中, \begin{document}$N$\end{document}表示星座中卫星的数目。

星座中的每颗卫星都可以提供对地的覆盖服务。将卫星\begin{document}$S$\end{document}在\begin{document}$t$\end{document}时刻的对地覆盖范围记作\begin{document}$\varLambda_{S}(t)$\end{document}, 将星座\begin{document}$\boldsymbol{C}$\end{document}在\begin{document}$t$\end{document}时刻的总对地覆盖范围记作\begin{document}$\varLambda_{\boldsymbol{C}}(t)$\end{document}, 则

令\begin{document}$R$\end{document}为卫星星座要服务的地面区域。如果在\begin{document}$t$\end{document}时刻, 区域\begin{document}$R$\end{document}内的一点\begin{document}$P$\end{document}包含于星座\begin{document}$\boldsymbol{C}$\end{document}在\begin{document}$t$\end{document}时刻的对地覆盖范围, 即\begin{document}$P \in \varLambda_{\boldsymbol{C}}(t)$\end{document}, 则称星座\begin{document}$\boldsymbol{C}$\end{document}在\begin{document}$t$\end{document}时刻可对\begin{document}$P$\end{document}点覆盖。则星座\begin{document}$\boldsymbol{C}$\end{document}在\begin{document}$t$\end{document}时刻可对区域\begin{document}$R$\end{document}的瞬时覆盖范围可表示为\begin{document}$\varLambda_{\boldsymbol{C}}(t) \cap R_{\circ}$\end{document}

将星座\begin{document}$\boldsymbol{C}$\end{document}在\begin{document}$t$\end{document}时刻对区域\begin{document}$R$\end{document}的瞬时覆盖面积与区域\begin{document}$R$\end{document}的总面积之比, 称作星座\begin{document}$\boldsymbol{C}$\end{document}在\begin{document}$t$\end{document}时刻对区域\begin{document}$R$\end{document}的瞬时覆盖率, 记作\begin{document}$\eta(t)$\end{document}。则

式中, \begin{document}$m[R]$\end{document}表示区域\begin{document}$R$\end{document}的面积度量。

通讯与导航星座等高实时性的星座往往需要星座\begin{document}$\boldsymbol{C}$\end{document}在仿真时段\begin{document}$\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}对目标时时刻刻都有覆盖, 将这种要求称作连续覆盖要求。对于地面一点\begin{document}$P$\end{document}, 如果\begin{document}$\forall t \in\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}, 都满足\begin{document}$P \in \varLambda_{\boldsymbol{C}}(t)$\end{document}, 则称星座\begin{document}$\boldsymbol{C}$\end{document}在仿真时段\begin{document}$\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}内对\begin{document}$P$\end{document}点连续性覆盖。将星座\begin{document}$\boldsymbol{C}$\end{document}在\begin{document}$\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}时段内连续覆盖范围记作\begin{document}$\varLambda_{\boldsymbol{C}}\left(\underline{\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]}\right)$\end{document}。则有

将星座\begin{document}$\boldsymbol{C}$\end{document}在\begin{document}$\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}时段内对区域\begin{document}$R$\end{document}的连续覆盖范围的面积与区域\begin{document}$R$\end{document}的总面积之比, 称作星座\begin{document}$\boldsymbol{C}$\end{document}在\begin{document}$\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}时段对区域\begin{document}$R$\end{document}的连续覆盖率, 记作\begin{document}$\eta\left(\underline{\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]}\right)$\end{document}。则

遥感类卫星星座往往对于数据实时性要求不是很高。此时通常需要星座\begin{document}$\boldsymbol{C}$\end{document}在某仿真时段\begin{document}$\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}能够对目标区域访问1次即可, 将这类覆盖要求称作累积覆盖要求。对于地面一点\begin{document}$P$\end{document}, 如果\begin{document}$\exists t \in\left[t_{\mathrm{s}}\right.$\end{document}, \begin{document}$\left.t_{\mathrm{e}}\right]$\end{document}, 使得\begin{document}$P \in \varLambda_{\boldsymbol{C}}(t)$\end{document}, 则称星座\begin{document}$\boldsymbol{C}$\end{document}在仿真时段\begin{document}$\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}内对\begin{document}$P$\end{document}点累积性覆盖。将星座\begin{document}$\boldsymbol{C}$\end{document}在仿真时段\begin{document}$\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}的累积覆盖范围记作\begin{document}$\varLambda_{\boldsymbol{C}}\left(\overline{\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]}\right)$\end{document}。则

将星座\begin{document}$\boldsymbol{C}$\end{document}在\begin{document}$\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}时段内对区域\begin{document}$R$\end{document}的累积覆盖范围的面积与区域\begin{document}$R$\end{document}的总面积之比, 称作星座\begin{document}$\boldsymbol{C}$\end{document}在\begin{document}$\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}时段对区域\begin{document}$R$\end{document}的累积覆盖率, 记作\begin{document}$\eta\left(\overline{\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]}\right)$\end{document}。则

在(3), (5), (7)式中, 覆盖率都定义为面积之比, 而非传统网格点法的网格点数目之比。该策略能够使得算法在处理靠近极区或者复杂区域边界时, 不会因为网格权值的不统一带来结果偏差。

三角网剖分法是一类经典的星座对地覆盖问题求解算法。对于地球表面\begin{document}$G$\end{document}, 以\begin{document}$t$\end{document}时刻星座在地球表面的投影\begin{document}$\bar{C}(t)$\end{document}为顶点, 按照球面Delaunay划分规则, 可将地球表面划分为若干球面三角形。将划分得到的第\begin{document}$k$\end{document}个球面三角形记作\begin{document}$D_{k}$\end{document}, 球面三角形的总数目为\begin{document}$M$\end{document}, 则

式中：\begin{document}$[\cdot]$\end{document}是一个球面面积测度函数；\begin{document}$m[R]$\end{document}表示球面区域\begin{document}$R$\end{document}的球面面积。则称\begin{document}$\left\{D_{k}\right\}$\end{document}是对球面的一个三角剖分。

网格法是对传统网格点法的改进: 摒弃以蒙特卡洛采样为核心的随机求解过程, 采用分治法将区域划分为网格进行确定性计算。相较于网格点法, 网格法避免了球面采样不均导致的计算偏差, 并能给出当前精度下的理论误差范围。

三角网剖分法计算高效, 但仅适用于全球覆盖分析, 无法处理纬度带或球面圆等非全球目标。此外, 该方法仅能判断是否实现全球完全覆盖, 无法计算不完全覆盖时的实际覆盖率。

网格法的主要局限在于覆盖判定计算复杂, 且高精度需求时(网格粒度小)会导致网格数量激增, 显著降低计算效率。

为此, 本文提出融合策略: 对三角网剖分法可处理的球面三角形直接应用该方法; 对其无法处理的复杂区域(如非全球目标), 则采用网格法精细化计算。该混合方法结合了两者优势: 兼具网格法的普适性, 同时通过算法选择性调用提升整体效率。此即基于Delaunay三角网的多粒度分层网格划分多星对地覆盖计算方法的核心思想。

2 覆盖目标图元划分及覆盖状态判定

2.1 球面三角形的确定状态与未定状态

设\begin{document}$R$\end{document}为任意球面区域, 经三角网剖分得到球面三角网集合\begin{document}$\left\{D_{k}(t)\right\}$\end{document}(时间无关时简记\begin{document}$\left\{D_{j}\right\}$\end{document})。对任意\begin{document}$D_{k} \in\left\{D_{j}\right\}$\end{document}, 其与\begin{document}$R$\end{document}的空间关系记作\begin{document}$\varTheta\left(D_{k}, R\right)$\end{document}, 分为3类：①\begin{document}$D_{k}$\end{document}完全包含于\begin{document}$R$\end{document}；②\begin{document}$D_{k}$\end{document}部分包含于\begin{document}$R$\end{document}；③\begin{document}$D_{k}$\end{document}与\begin{document}$R$\end{document}无交集。本文定义符号"部分包含"为" \begin{document}$\mid=$\end{document}"。则3种关系采用集合中的符号可分别表示为：\begin{document}$D_{k} \subset R, D_{k} \mid=R$\end{document}以及\begin{document}$D_{k} \subset G \backslash R$\end{document}, 其中\begin{document}$G$\end{document}表示整个地球表面, \begin{document}$G \backslash R$\end{document}表示区域\begin{document}$R$\end{document}对整个地球表面的补集。则

当\begin{document}$D_{k} \subset G \backslash R$\end{document}, 表明该球面三角形不属于区域内部, 则可以将其移出要分析的三角网集合

类似地, 星座对球面三角形\begin{document}$D_{k}$\end{document}的覆盖关系记作\begin{document}$\varTheta\left(D_{k}, \varLambda_{\boldsymbol{C}}\right)$\end{document}。则\begin{document}$\varTheta\left(D_{k}, \varLambda_{\boldsymbol{C}}\right)$\end{document}同样可以分为3类：星座对\begin{document}$D_{k}$\end{document}完全覆盖；星座对\begin{document}$D_{k}$\end{document}部分覆盖；星座对\begin{document}$D_{k}$\end{document}无覆盖。实际情况中, \begin{document}$D_{k}$\end{document}是以卫星的星下点位置为顶点, 因此实际不存在无覆盖情形。

在形式上, 表示\begin{document}$\varTheta\left(D_{k}, R\right)$\end{document}与\begin{document}$\varTheta\left(D_{k}, \varLambda_{\boldsymbol{C}}\right)$\end{document}时, 使用如(12)式形式表示, 比如当\begin{document}$\varTheta\left(D_{k}, R\right)$\end{document}为\begin{document}$D_{k} \mid=R$\end{document}时, 可表示为

当\begin{document}$\varTheta\left(D_{k}, R\right)=\left[D_{k} \mid=R\right]$\end{document}时, 三角网法无法量化\begin{document}$D_{k}$\end{document}中属于\begin{document}$R$\end{document}的面积。当\begin{document}$\varTheta\left(D_{k}, R\right) \neq\left[D_{k} \subset G \backslash R\right]$\end{document}且\begin{document}$\varTheta\left(D_{k}, \varLambda_{\boldsymbol{C}}\right)=\left[D_{k} \mid=\varLambda_{\boldsymbol{C}}\right]$\end{document}时, 无法量化\begin{document}$D_{k}$\end{document}中被覆盖的面积。上述2类状态的组合, 统称为未定状态。

当\begin{document}$\varTheta\left(D_{k}, R\right)=\left[D_{k} \subset R\right]$\end{document}且\begin{document}$\varTheta\left(D_{k}, \varLambda_{\boldsymbol{C}}\right)=\left[D_{k} \subset\right.$\end{document} \begin{document}$\varLambda_{\boldsymbol{C}}$\end{document}]时, \begin{document}$D_{k}$\end{document}的覆盖状态完全确定, 将该情况称作"确定状态"。

\begin{document}$D_{k}$\end{document}处于确定状态或者未定状态的情况组合, 如表 1所示。

表1

Dk所处状态的情况组合

2.2 球面三角形的区域覆盖状态及星座覆盖状态的判定

\begin{document}$D_{k}$\end{document}与区域\begin{document}$R$\end{document}关系\begin{document}$\varTheta\left(D_{k}, R\right)$\end{document}的计算, 可以借助于球面多边形的关系判定算法来实现。

算法1   球面三角形\begin{document}$D_{k}$\end{document}与区域\begin{document}$R$\end{document}的关系判定

输入   球面三角形\begin{document}$D_{k}$\end{document}, 区域\begin{document}$R$\end{document}

输出   \begin{document}$\varTheta\left(D_{k}, R\right)$\end{document}的结果

步骤1   对于\begin{document}$D_{k}$\end{document}, 将其最小经纬度框包围记作\begin{document}$U\left[D_{k}\right]$\end{document}, 对于\begin{document}$R$\end{document}, 其最小经纬度框包围为\begin{document}$U[R]$\end{document}。如果\begin{document}$U\left[D_{k}\right] \cap U[R]=\varnothing$\end{document}, 则\begin{document}$D_{k}$\end{document}与\begin{document}$R$\end{document}关系为\begin{document}$D_{k} \subset$\end{document} \begin{document}$G \backslash R$\end{document}, 算法结束；否则, 跳转到步骤2。

步骤2   对\begin{document}$D_{k}$\end{document}, 将其边界集合记作\begin{document}$\partial D_{k}$\end{document}, 则\begin{document}$\partial D_{k}$\end{document}是由多个球面大圆弧段组成的集合。同理, 将区域\begin{document}$R$\end{document}的边界集合记作\begin{document}$\partial R$\end{document}, 并且\begin{document}$\partial R$\end{document}是由多个球面大圆弧段或小圆弧段组成的集合。如果\begin{document}$\partial D_{k} \cap \partial R \neq \varnothing$\end{document}, 则球面三角形\begin{document}$D_{k}$\end{document}与区域\begin{document}$R$\end{document}的关系为\begin{document}$D_{k} \mid=R$\end{document}, 算法结束；否则, 跳转到步骤3。

步骤3   在\begin{document}$D_{k}$\end{document}内部任取一点\begin{document}$P$\end{document}, 如果\begin{document}$P \in R$\end{document}, 则\begin{document}$D_{k} \subset R$\end{document}, 算法结束；否则跳转到步骤4。

步骤4   在\begin{document}$R$\end{document}内部任取一点\begin{document}$Q$\end{document}, 判断\begin{document}$Q$\end{document}与\begin{document}$D_{k}$\end{document}的关系。如果\begin{document}$Q \in D_{k}$\end{document}, 则表明\begin{document}$R$\end{document}是\begin{document}$D_{k}$\end{document}的子集, 但在\begin{document}$\varTheta\left(D_{k}, R\right)$\end{document}关系中, 并没有将其单独化作一个独立的分类, 因此, 在球面三角形\begin{document}$D_{k}$\end{document}与区域\begin{document}$R$\end{document}的关系中被判定为\begin{document}$D_{k} \mid=R$\end{document}；否则\begin{document}$D_{k} \subset G \backslash R$\end{document}。

对于球面三角形\begin{document}$D_{k}$\end{document}与星座的关系判定, 令\begin{document}$D_{k}$\end{document}的球面外接圆半径为\begin{document}$r_{k}$\end{document}, 星载传感器的对地覆盖圆半径为\begin{document}$\alpha$\end{document}。如果对任意球面三角形\begin{document}$D_{k}$\end{document}, 都有\begin{document}$r_{k}<\alpha$\end{document}, 则\begin{document}$D_{k} \subset \varLambda_{\boldsymbol{C}}$\end{document}。然而当\begin{document}$r_{k}>\alpha$\end{document}时, 却并不能意味着\begin{document}$D_{k} \mid=\varLambda_{\boldsymbol{C}}$\end{document}一定成立。由于球面三角形的特殊性, 在某些情况下, 当球面三角形的外心在球面三角形外部时, 可能出现当\begin{document}$r_{k}>\alpha$\end{document}时, 依然满足\begin{document}$D_{k} \mid=\varLambda_{\boldsymbol{C}}$\end{document}。

球面三角形\begin{document}$D_{k}$\end{document}与星座覆盖范围\begin{document}$\varLambda_{\boldsymbol{C}}$\end{document}的关系判定算法如算法2所示。

算法2   球面三角形\begin{document}$D_{k}$\end{document}与星座覆盖范围\begin{document}$\varLambda_{\boldsymbol{C}}$\end{document}的关系判定

输入   球面三角形\begin{document}$D_{k}$\end{document}, 传感器覆盖圆半径\begin{document}$\alpha$\end{document}

输出   \begin{document}$\varTheta\left(D_{k}, \varLambda_{\boldsymbol{C}}\right)$\end{document}的结果

步骤1  计算球面三角形\begin{document}$D_{k}$\end{document}的球面外接圆半径\begin{document}$r_{k}$\end{document}。如果\begin{document}$r_{k}<\alpha$\end{document}, 则\begin{document}$D_{k}$\end{document}与区域覆盖范围\begin{document}$\varLambda_{\boldsymbol{C}}$\end{document}的关系为\begin{document}$D_{k} \subset \varLambda_{\boldsymbol{C}}$\end{document}, 算法结束；否则, 跳转到步骤2。

步骤2  对球面三角形对应的3颗卫星中的任意2颗卫星进行如下计算：任取2颗卫星, 判断二者的覆盖圆边界的交点。如果2颗卫星的覆盖圆边界相交, 且交点落在\begin{document}$D_{k}$\end{document}的内部, 而且该交点不被第3颗卫星覆盖, 则\begin{document}$D_{k}$\end{document}与区域覆盖范围\begin{document}$\varLambda_{\boldsymbol{C}}$\end{document}的关系为\begin{document}$D_{k} \mid=\varLambda_{\boldsymbol{C}}$\end{document}, 算法结束。若任意2颗卫星都不满足上述条件, 则跳转到步骤3。

步骤3  对球面三角形对应的3颗卫星中的每颗卫星进行如下计算：对每颗卫星, 计算其覆盖圆边界与球面三角形边界的交点。如果存在1个交点, 不被其他2颗卫星覆盖, 则球面三角形\begin{document}$D_{k}$\end{document}与区域覆盖范围\begin{document}$\varLambda_{\boldsymbol{C}}$\end{document}的关系为\begin{document}$D_{k} \mid=\varLambda_{\boldsymbol{C}}$\end{document}, 算法结束。若每颗卫星都不满足上述条件, 则球面三角形\begin{document}$D_{k}$\end{document}与区域覆盖范围\begin{document}$\varLambda_{\boldsymbol{C}}$\end{document}的关系为\begin{document}$D_{k} \subset \varLambda_{\boldsymbol{C}}$\end{document}。

2.3 球面三角形的不确定经纬度框计算

对于球面三角形\begin{document}$D_{k}$\end{document}, 其星座覆盖状态如果为\begin{document}$D_{k} \mid=\varLambda_{\boldsymbol{C}}$\end{document}, 则希望在区域\begin{document}$D_{k}$\end{document}内得到一个经纬度框, 记作\begin{document}$H\left(D_{k}\right)$\end{document}, 使得在该球面三角形\begin{document}$D_{k}$\end{document}内所有不被星座覆盖的区域, 都包含于\begin{document}$H\left(D_{k}\right)$\end{document}。

对于\begin{document}$H\left(D_{k}\right)$\end{document}的选择, 有多种不同的选择, 比如, 可以选择\begin{document}$D_{k}$\end{document}的最小经纬度包围\begin{document}$U\left[D_{k}\right]$\end{document}。但过大范围\begin{document}$H\left(D_{k}\right)$\end{document}的选择, 会使得原本不需要星座覆盖状态判定的网格要重新判定, 从而影响算法效率。因此, 在选择\begin{document}$H\left(D_{k}\right)$\end{document}时, 做如下要求：\begin{document}$H\left(D_{k}\right)$\end{document}为包围球面三角形\begin{document}$D_{k}$\end{document}内所有不被星座覆盖区域的最小经纬度框。

由此, \begin{document}$H\left(D_{k}\right)$\end{document}的求解算法如下。

算法3   球面三角形的最小不确定经纬度框\begin{document}$H\left(D_{k}\right)$\end{document}求解算法判定

输入   球面三角形\begin{document}$D_{k}$\end{document}, 传感器覆盖圆半径\begin{document}$\alpha$\end{document}

输出   球面三角形的最小不确定经纬度框\begin{document}$H\left(D_{k}\right)$\end{document}

步骤1  判定球面三角形\begin{document}$D_{k}$\end{document}的星座覆盖状态。如果\begin{document}$D_{k} \subset \varLambda_{\boldsymbol{C}}$\end{document}, 则\begin{document}$H\left(D_{k}\right)$\end{document}为空, 算法结束。

步骤2  创建可用于保存地面点的集合\begin{document}$\boldsymbol{V}$\end{document}, 并将其置为空集。

步骤3  对球面三角形对应的3颗卫星进行如下计算：任取2颗卫星, 判断二者的覆盖圆边界的交点。若边界相交且交点落在\begin{document}$D_{k}$\end{document}的内部, 而且该交点不被第3颗卫星覆盖, 则将该交点加入\begin{document}$\boldsymbol{V}$\end{document}中。

步骤4  对球面三角形对应的3颗卫星进行如下计算：对每颗卫星, 计算其覆盖圆边界与球面三角形边界的交点。若交点不被其他2颗卫星覆盖, 则将该交点加人\begin{document}$\boldsymbol{V}$\end{document}中。

步骤5  判断北极点是否包含于\begin{document}$D_{k}$\end{document}中, 若包含则计算\begin{document}$\boldsymbol{V}$\end{document}中所有点的最小纬度值, 记作\begin{document}$\varphi_{\text {min }}$\end{document}, 则\begin{document}$H\left(D_{k}\right)$\end{document}为纬度从\begin{document}$\varphi_{\text {min }} \sim {\rm{\mathsf{π}}} / 2$\end{document}的北极极冠。同理判断南极点是否包含于\begin{document}$D_{k}$\end{document}中, 若包含则计算\begin{document}$\boldsymbol{V}$\end{document}中所有点的最大纬度值, 记作\begin{document}$\varphi_{\text {max }}$\end{document}, 则\begin{document}$H\left(D_{k}\right)$\end{document}为纬度从\begin{document}$-{\rm{\mathsf{π}}} / 2 \sim \varphi_{\text {min }}$\end{document}的南极极冠。

步骤6  判断集合\begin{document}$\boldsymbol{V}$\end{document}中的点是否跨越\begin{document}$2 {\rm{\mathsf{π}}}$\end{document}边界, 也就是有部分点的经度值接近\begin{document}$2 {\rm{\mathsf{π}}}$\end{document}, 有部分点的经度值接近0。如果集合\begin{document}$\boldsymbol{V}$\end{document}中的点跨越\begin{document}$2 {\rm{\mathsf{π}}}$\end{document}边界, 则将\begin{document}$\boldsymbol{V}$\end{document}中点的经纬度表示从\begin{document}$[0, 2 {\rm{\mathsf{π}}}]$\end{document}区间, 转换为\begin{document}$[-{\rm{\mathsf{π}}}$\end{document}, \begin{document}${\rm{\mathsf{π}}}]$\end{document}。然后以经纬度为坐标, 计算集合\begin{document}$V$\end{document}的经纬度范围, 从而得到\begin{document}$H\left(D_{k}\right)$\end{document}。

2.4 网格在仿真时段内的星座覆盖状态判定

某时刻下, 三角网与星座的关系可分为3类。网格同理, 其与星座之间的关系, 也可分为3类：网格包含于星座；网格部分包含于星座；网格与星座不相交。本文采用相同的符号表示。如网格\begin{document}$N_{j}$\end{document}与星座的关系可以表示为

而对一个时段而言, 同样可以分析网格与星座之间的关系。将星座\begin{document}$\boldsymbol{C}$\end{document}在仿真时段\begin{document}$\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}内对网格\begin{document}$N_{j}$\end{document}的连续性覆盖关系表示为\begin{document}$\varTheta\left(N_{j}\right.$\end{document}, \begin{document}$\left.\varLambda_{\boldsymbol{C}}\left(\underline{\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]}\right)$\end{document}。则根据\begin{document}$\varLambda_{\boldsymbol{C}}\left(\underline{\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]}\right)$\end{document}的基本定义, 有如下判定规则：

当\begin{document}$\exists t \in\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}, 使得\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}(t)\right)=\left[N_{j} \subset\right.$\end{document} \begin{document}$\left.G \backslash \varLambda_{\boldsymbol{C}}(t)\right]$\end{document}, 则\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}\left(\underline{\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]}\right)=\left[N_{j} \subset G \backslash \varLambda_{\boldsymbol{C}}(t)\right]$\end{document}；

当对\begin{document}$\forall t \in\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}, 都有\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}(t)\right) \neq$\end{document} \begin{document}$\left[N_{j} \subset G \backslash \varLambda_{\boldsymbol{C}}(t)\right]$\end{document}, 并且\begin{document}$\exists t \in\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}, 使得\begin{document}$\varTheta\left(N_{j}\right.$\end{document}, \begin{document}$\left.\varLambda_{\boldsymbol{C}}(t)\right)=\left[N_{j} \mid=\varLambda_{\boldsymbol{C}}(t)\right]$\end{document}, 则\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}\left(\underline{\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]}\right)=$\end{document} \begin{document}$\left[N_{j} \mid=\varLambda_{\boldsymbol{C}}(t)\right]$\end{document}。

当对\begin{document}$\forall t \in\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}, 都有\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}(t)\right)=\left[N_{j} \subset\right.$\end{document} \begin{document}$\left.\varLambda_{\boldsymbol{C}}(t)\right]$\end{document}, 则\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}\left(\underline{\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]}\right)=\left[N_{j} \subset \varLambda_{\boldsymbol{C}}(t)\right]$\end{document}。

将星座\begin{document}$\boldsymbol{C}$\end{document}在仿真时段\begin{document}$\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}内对网格\begin{document}$N_{j}$\end{document}的累积性覆盖关系表示为\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}\left(\overline{\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]}\right)\right)$\end{document}。则根据\begin{document}$\varLambda_{\boldsymbol{C}}\left(\overline{\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]}\right)$\end{document}的基本定义, 有如下判定规则：

当\begin{document}$\exists t \in\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}, 使得\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}(t)\right)=\left[N_{j} \subset\right.$\end{document} \begin{document}$\left.\varLambda_{\boldsymbol{C}}(t)\right]$\end{document}, 则\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}\left(\overline{\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]}\right)\right)=\left[N_{j} \subset \varLambda_{\boldsymbol{C}}(t)\right]$\end{document}；

当对\begin{document}$\forall t \in\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}, 都有\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}(t)\right) \neq\left[N_{j} \subset\right.$\end{document} \begin{document}$\left.\varLambda_{\boldsymbol{C}}(t)\right]$\end{document}, 并且\begin{document}$\exists t \in\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}, 使得\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}(t)\right)=$\end{document} \begin{document}$\left[N_{j} \mid=\varLambda_{\boldsymbol{C}}(t)\right]$\end{document}, 则\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}\left(\overline{\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]}\right)\right)=\left[N_{j} \mid=\right.$\end{document} \begin{document}$\left.\varLambda_{\boldsymbol{C}}(t)\right]$\end{document}。

当对\begin{document}$\forall t \in\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}, 都有\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}(t)\right)=\left[N_{j} \subset G \backslash\right.$\end{document} \begin{document}$\left.\varLambda_{\boldsymbol{C}}(t)\right]$\end{document}, 则\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}\left(\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]\right)\right)=\left[N_{j} \subset G \backslash \varLambda_{\boldsymbol{C}}(t)\right]$\end{document}。

3 基于三角网剖分的多粒度分层网格覆盖法

3.1 星地瞬时性覆盖率计算

当球面三角形的覆盖状态未定时, 需采用网格法对其进行覆盖分析, 计算其内部被星座覆盖的面积占比。

因此, 本文提出基于Delaunay三角网和多粒度分层网格划分混合的求解算法, 具体流程见算法4。

算法4   星座对区域目标的瞬时覆盖问题求解算法

输入   星座\begin{document}$\boldsymbol{C}$\end{document}, 时刻\begin{document}$t$\end{document}, 传感器覆盖圆半径\begin{document}$\alpha$\end{document}, 区域\begin{document}$R$\end{document}

输出   星座\begin{document}$\boldsymbol{C}$\end{document}在时刻\begin{document}$t$\end{document}的瞬时覆盖率

步骤1  根据网格法, 将区域\begin{document}$R$\end{document}进行划分, 将不包含于区域的网格去除, 得到网格集合\begin{document}$\boldsymbol{N}=\left\{N_{1}, N_{2}\right.$\end{document}, \begin{document}$\left.\cdots, N_{j}, \cdots, N_{K}\right\}$\end{document}, 其中\begin{document}$K$\end{document}为网格集合中的网格总数。

步骤2  通过三角网剖分法, 得到\begin{document}$t$\end{document}时刻对全球的三角网集合\begin{document}$\boldsymbol{D}(t)=\left\{D_{1}(t), D_{2}(t), \cdots, D_{j}(t), \cdots\right.$\end{document}, \begin{document}$\left.D_{k}(t)\right\}$\end{document}, 其中\begin{document}$k=1, 2, \cdots, M$\end{document}。

步骤3   对\begin{document}$\boldsymbol{D}(t)$\end{document}中的每个球面三角形\begin{document}$D_{k}$\end{document}, 判断其与区域的关系\begin{document}$\varTheta\left(D_{k}, R\right)$\end{document}。将所有\begin{document}$\varTheta\left(D_{k}, R\right)=$\end{document} \begin{document}$\left[D_{k} \subset G \backslash R\right]$\end{document}球面三角形, 从三角网集合中去除, 得到新的球面三角形集合, 记作\begin{document}$\boldsymbol{D}(t)$\end{document}。

步骤4  对\begin{document}$\boldsymbol{D}(t)$\end{document}中的每个球面三角形, 判定其与星座的关系\begin{document}$\varTheta\left(D_{k}, \varLambda_{\boldsymbol{C}}\right)$\end{document}。

步骤5  用算法3计算所有处于未定覆盖状态的球面三角形\begin{document}$D_{k}$\end{document}的最小不确定经纬度框\begin{document}$H\left(D_{k}\right)$\end{document}。

步骤6  对\begin{document}$\boldsymbol{N}$\end{document}中的每个网格\begin{document}$N_{j}$\end{document}, 如果存在1个\begin{document}$\boldsymbol{H}\left(D_{k}\right)$\end{document}, 使得\begin{document}$N_{j} \cap \boldsymbol{H}\left(D_{k}\right) \neq \varnothing$\end{document}, 则\begin{document}$N_{j}$\end{document}加人未定覆盖状态网格集合中。如果对任何\begin{document}$\boldsymbol{H}\left(D_{k}\right)$\end{document}, 都有\begin{document}$N_{j} \cap$\end{document} \begin{document}$\boldsymbol{H}\left(D_{k}\right)=\varnothing$\end{document}, 则\begin{document}$N_{j}$\end{document}可被直接判定为网格被星座完全覆盖, 即\begin{document}$\varTheta\left(N_{j}, \varLambda_{\boldsymbol{C}}\right)=\left[N_{j} \subset \varLambda_{\boldsymbol{C}}\right]$\end{document}。

步骤7  对每个三角网的覆盖状况进行统计, 得到星座\begin{document}$\boldsymbol{C}$\end{document}在时刻\begin{document}$t$\end{document}的瞬时覆盖率。

3.2 星地时段性覆盖指标计算

时段性覆盖含连续性覆盖与累积覆盖2类, 均需分析区域内点P在各时刻的覆盖状态。然而, 三角网剖分法依据卫星星下点动态划分地表, 会导致不同时刻生成的球面三角网结构变化。例如, 点P在时刻t1属于球面三角形Dk(t1), 而在时刻t2则可能属于另一个无关的的球面三角形Dj(t2)。这种动态性使得时段性覆盖分析面临挑战: 需要从无直接关联的球面三角形中提取并关联同一点的覆盖状态数据。为满足这一要求, 本文提出依据目标区域特征划分固定网格, 并构建从任意动态球面三角形到该固定网格的映射关系, 从而有效支撑时段性覆盖分析。具体流程见算法5。

算法5   星座对区域目标的时段性覆盖问题求解算法

输入   星座 \begin{document}$\boldsymbol{C}$\end{document}, 时间段 \begin{document}$\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}, 传感器覆盖圆半径 \begin{document}$\alpha$\end{document}, 区域 \begin{document}$R$\end{document}

输出   星座 \begin{document}$\boldsymbol{C}$\end{document}在时刻 \begin{document}$t$\end{document}的累积性覆盖率或连续性覆盖率

步骤1  根据网格法, 将区域 \begin{document}$R$\end{document}进行划分, 将不包含于区域的网格去除, 得到网格集合 \begin{document}$\boldsymbol{N}$\end{document}。

步骤2  将时间段 \begin{document}$\left[t_{\mathrm{s}}, t_{\mathrm{e}}\right]$\end{document}按照间隔 \begin{document}$\Delta t$\end{document}对其离散化, 得到离散化的时刻 \begin{document}$\left\{t_{0}, t_{1}, \cdots, t_{j}, \cdots, t_{L}\right\}$\end{document}, 其中对任意 \begin{document}$k \in\{1, 2 \cdots, L\}$\end{document}都有 \begin{document}$t_{k}-t_{k-1}=\Delta t$\end{document}, 并且 \begin{document}$t_{0}=$\end{document} \begin{document}$t_{\mathrm{s}}, t_{L}=t_{\mathrm{e}}$\end{document}。

步骤3  对每个时刻, 通过三角网剖分法, 得到该时刻的三角网集合 \begin{document}$\left\{D_{k}\left(t_{j}\right)\right\}$\end{document}。

步骤4   通过算法4中的步骤, 得到该时刻下网格集合 \begin{document}$\boldsymbol{N}$\end{document}中的每个网格与星座的关系。

步骤5  遍历所有时刻, 得到网格集合 \begin{document}$\boldsymbol{N}$\end{document}中每个网格在每个时刻与星座的关系, 并以此判定网格在整个仿真时段与星座的关系。

步骤6  统计所有网格的覆盖状态, 得到星座对区域覆盖的累积性覆盖率或者连续性覆盖率。

3.3 算法性能分析

该算法对瞬时和时段性覆盖问题中的网格覆盖状态判定均分为2类。

第1类  若网格不与任何球面三角形的不确定经纬度框相交, 则可基于三角网剖分信息直接判定为覆盖状态, 称为“第1类网格”。

第2类  若网格与某不确定框相交, 则需通过网格法进行状态判定, 称为“第2类网格”。

由于网格覆盖判定是计算中最耗时的环节, 第1类网格的占比(κ)直接决定了算法的整体效率。设三角网剖分法与网格法的计算效率分别为β1与β2。则算法效率β近似满足(14)式。

由于网格法的计算效率显著低于三角网剖分法, (14)式中κ值成为算法效率的关键决定因素。当三角网中多数球面三角形处于未定覆盖状态时, κ趋近于0, 算法效率接近网格法, 丧失优势; 反之, 若多数三角形覆盖状态确定, κ趋近于1, 算法效率显著优于网格法。在精度方面, 网格法的精度随划分粒度增加而提高, 但计算成本急剧上升; 本文中提出的三角网剖分与多粒度分层网格划分混合计算方法同样受网格粒度影响精度与效率。具体粒度选择策略见文献[28]。

4 数值仿真分析

为验证算法有效性, 开展数值仿真实验。瞬时覆盖问题仿真周期设为[2022-01-01 00∶00∶00, 2022-01-01 00∶10∶00]。采用40/4/1构型Walker星座, 卫星高度1 300 km, 圆轨道倾角45°, 除中心引力外仅考虑J2摄动。所有卫星搭载同型简单圆锥体传感器(无侧摆)。针对累积覆盖与连续覆盖两类问题, 分别设置传感器参数以控制输出规模。验证区域包含2类目标:

覆盖目标1  全球。验证大范围区域性能。

覆盖目标2  美洲大陆。由3 369个球面点构成的球面不规则凹多边形, 验证复杂多边形区域性能。

4.1 瞬时覆盖问题

瞬时覆盖问题中传感器半视场角设为52°。

图 1显示星座对目标1瞬时覆盖下球面三角形的状态。红色为完全覆盖, 无色为部分覆盖, 蓝线标示三角剖分边界。

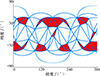thumbnail 图1

对目标1的瞬时覆盖下球面三角形的状态

图 2显示星座对目标2瞬时覆盖下球面三角形的状态。其中红色和绿色区域为部分包含于目标的三角形(红色为完全覆盖, 绿色为部分覆盖), 无色区域为无关三角形(不计入分析)。

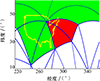thumbnail 图2

对目标2瞬时覆盖下球面三角形的状态

图 3目标1瞬时覆盖下球面三角形的不确定性经纬度框纬度框。图 4显示星座对目标2瞬时覆盖下, 通过算法3生成对所有未定状态的球面三角形的不确定性经纬度框。其中绿色区域标示未定状态三角形的不确定框, 无色区域为已判定完全覆盖区域。

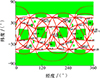thumbnail 图3

显示星座对目标1瞬时覆盖下, 通过算法3生成对所有未定状态的球面三角形的不确定性经

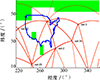thumbnail 图4

目标2瞬时覆盖下球面三角形的不确定性经纬度框

采用本文算法(网格划分精度2°×2°)求解, 图 5显示星座对目标1瞬时覆盖下的网格状态, 蓝色网格为第1类网格(三角网法直接判定完全覆盖), 其余为第2类网格(绿色为网格法判定完全覆盖, 红色为部分覆盖, 黄色为无覆盖)。图 6为星座对目标2瞬时覆盖下的网格状态, 其着色规则同图 5, 无色区域为无关网格。

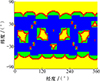thumbnail 图5

对目标1瞬时覆盖下的网格状态

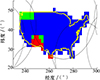thumbnail 图6

对目标2瞬时覆盖下的网格状态

(14) 式表明算法性能核心取决于κ值(第1类网格占比), κ值增大将直接提升算法效率。κ值主要受传感器覆盖圆半径调控, 其随半径的变化规律如图 7所示: 随着覆盖圆半径增加, κ值呈现单调递增趋势, 算法效率同步提升。每条κ值变化曲线均存在2个特征突变点——κ值从零跃升至非零的零突变点(约5°), 以及κ值趋于稳定收敛点。当覆盖半径小于零突变点时, 算法效率等同于传统网格法; 当覆盖半径超过收敛点, 效率增长趋于平稳。

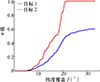thumbnail 图7

瞬时覆盖下κ值随着传感器覆盖圆半径的变化曲线

4.2 累积覆盖问题

针对累积覆盖问题, 设置星座传感器张角为45°。目标1与目标2的累积覆盖范围分布分别如图 8~9所示, 图中颜色语义与前述瞬时覆盖分析保持一致。图 8与图 9中蓝色区域的占比直接反映算法效率κ值。与瞬时覆盖问题一致, 累积覆盖问题的κ值随传感器张角增大而单调递增。图 10展示了目标1与目标2的κ值随覆盖圆半径变化曲线, 较之瞬时覆盖, 累积覆盖的0突变点与收敛点均显著左移。

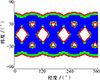thumbnail 图8

对目标1的累积覆盖范围

thumbnail 图9

对目标2的累积覆盖范围

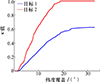thumbnail 图10

累积覆盖下κ值随着覆盖圆半径变化的曲线

4.3 连续覆盖问题

针对连续覆盖问题, 设置传感器半视场角为52°。星座在仿真时段内对目标1与目标2的连续覆盖范围分布分别如图 11~12所示, 图中颜色语义沿用前述规范。

thumbnail 图11

对目标1的连续覆盖范围结果

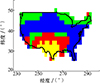thumbnail 图12

对目标2的连续覆盖范围结果

图 13展示2类目标的κ值随覆盖圆半径变化曲线，相较于瞬时覆盖, 连续覆盖的0突变点与收敛点均显著右移。

thumbnail 图13

连续覆盖下κ值随着覆盖圆半径变化的曲线

5 结论

本文提出一种基于Delaunay三角网和多粒度分层网格划分混合的多星对地覆盖计算方法, 通过球面三角剖分与精确网格评估策略, 构建了面向瞬时、连续及累积覆盖率的完整计算框架, 可高效处理不规则地面目标。实验表明, 当覆盖圆半径较小时, 算法效率接近纯网格法; 随半径增大效率显著提升。规则区域场景下κ值收敛于1, 此时算法在保持网格法求解能力的同时, 效率逼近三角网剖分法, 实现复杂覆盖问题的效率突破。

然而, 不规则区域受限于多粒度网格固有缺陷, κ收敛值小于1, 导致效率提升幅度受限。总体而言, 相较于传统三角网法或网格法, 本算法在各类覆盖场景中均展现出更优的求解速度与适应性, 尤其擅长处理复杂覆盖约束条件。

References

  1. SHEN Lirong, MAO Jia, LIU Zhiwei, et al. Coverage and visibility analysis of iridium and starlink constellations for autonomous navigation of aircraft[J]. Astronautical Systems Engineering Technology, 2024, 8(1): 48–57 (in Chinese) [Google Scholar]
  2. ORTORE E, CINELLI M, CIRCI C. A ground track-based approach to design satellite constellations[J]. Aerospace Science and Technology, 2017, 69: 458–464 [Google Scholar]
  3. DAI G, CHEN X, WANG M, et al. Analysis of satellite constellations for the continuous coverage of ground regions[J]. Journal of Spacecraft and Rockets, 2017, 54(6): 1294–1303 [NASA ADS] [CrossRef] [Google Scholar]
  4. WANG H, BAI S. A versatile method for target area coverage analysis with arbitrary satellite attitude maneuver paths[J]. Acta Astronautica, 2022, 194: 242–254 [Google Scholar]
  5. YAN Ye, REN Xuan, CHEN Lei. Criterion and algorithm of satellites coverage situation[J]. Journal of Astronautics, 1999, 20(2): 55–60 (in Chinese) [Google Scholar]
  6. ULYBYSHEV Y. General analysis method for discontinuous coverage satellite constellations[J]. Journal of Guidance, Control, and Dynamics, 2015, 12(38): 2475–2482 [Google Scholar]
  7. GONG Y, ZHANG S, PENG X. Quick coverage analysis of mega walker constellation based on 2D map[J]. Acta Astronautica, 2021, 188: 99–109 [Google Scholar]
  8. ZHANG Y, BAI S, HAN C. Geometric analysis of a constellation with a ground target[J]. Acta Astronautica, 2022, 191: 510–521 [Google Scholar]
  9. XU M, HUANG L. An analytic algorithm for global coverage of the revisiting orbit and its application to the CFOSAT satellite[J]. Astrophysics and Space Science, 2014, 352(2): 497–502 [Google Scholar]
  10. LYU Linli, XIAO Xinxin, FENG Guanhua, et al. Efficient algorithm for calculating coverage of mega-constellation[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(3): 426–436 (in Chinese) [Google Scholar]
  11. CHEN X, SONG Z, DAI G, et al. A general formal method for manifold coverage analysis of satellite constellations[J]. IEEE Trans on Aerospace and Electronic Systems, 2022, 58(2): 1462–1479 [Google Scholar]
  12. ZHOU M, SONG Z, DAI G, et al. Characteristic area-based method for continuous coverage analysis of satellites constellation[J]. IEEE Trans on Aerospace and Electronic Systems, 2023, 59(5): 7128–7139 [Google Scholar]
  13. CHEN Xiaoyu, DAI Guangming, CHEN Liang, et al. A method for constellation performance analysis based on spherical subdivision[J]. Journal of Astronautics, 2016, 37(10): 1246–1254 (in Chinese) [Google Scholar]
  14. WU Huanqin, WANG Maocai, SONG Zhiming, et al. A random error estimation method for satellites being launched into orbit based on ellipsoid theory[J]. Journal of Northwestern Polytechnical University, 2023, 41(4): 802–811. [Article] (in Chinese) [Google Scholar]
  15. JIAN Ping, ZOU Peng, XIONG Wei, et al. Improved grid method for analysis on coverage performance of staring sensors based LEO[J]. Journal of Air Force Engineering University, 2012, 13(3): 35–39 (in Chinese) [Google Scholar]
  16. HANG W, SHIMIZU S, YOSHIKAWA S, et al. Satellite constellation pattern optimization for complex regional coverage[J]. Journal of Spacecraft and Rockets, 2020, 57: 1309–1327 [Google Scholar]
  17. CHEN X, GU W, DAI G, et al., Data-driven collaborative scheduling method for multi-satellite data-transmission[J]. Tsinghua Science and Technology, 2024, 29(5): 1463–1480 [Google Scholar]
  18. RUAN Qiming, TAN Yuejin, LI Yongtai, et al. Using constraint satisfaction to cooperate satellites' activities for the mission of area target observation[J]. Journal of Astronautics, 2007, 28(1): 238–242 (in Chinese) [Google Scholar]
  19. SHAO X, ZHANG Z, WANG J, et al. NSGA-Ⅱ-based multi-objective mission planning method for satellite formation system[J]. Journal of Aerospace Technology and Management, 2016, 8(4): 451–458 [Google Scholar]
  20. LIU Huajun, CAI Bo, ZHU Qing. Self-adaptive planning method of imaging reconnaissance satellites area coverage[J]. Geomatics and Information Science of Wuhan University, 2017, 42(12): 1719–1725 (in Chinese) [Google Scholar]
  21. SONG Zhiming, LIU Haidong, CHEN Xiaoyu, et al. An efficient algorithm for solving the constellation-to-ground region coverage problem based on longitude strip division[J]. Journal of Northwestern Polytechnical University, 2021, 39(4): 919–929. [Article] (in Chinese) [Google Scholar]
  22. XU Yudong, ZHOU Jingbo, YIN Jiazhao, et al. Review of mission planning strategies and applications of earth observation satellites[J]. Radio Engineering, 2021, 51(8): 681–690 (in Chinese) [Google Scholar]
  23. ZHU W, HU X, XIA W, et al. A three-phase solution method for the scheduling problem of using earth observation satellites to observe polygon requests[J]. Computers Industrial Engineering, 2019, 130: 97–107 [Google Scholar]
  24. YANG Jiwei, FU Wei, HAN Li, et al. Regional target planning algorithm of satellite imaging based on global grid[J]. Spacecraft Engineering, 2021, 30(1): 31–38 (in Chinese) [Google Scholar]
  25. LI X. Two-archive2 algorithm for large-scale polygon targets observation scheduling problem[C]//Proceedings of the 2nd International Conference on Information Technology and Management Engineering, Shanghai, 2017: 23–24 [Google Scholar]
  26. XU Y, LIU X, HE R, et al. Multi-satellite scheduling framework and algorithm for very large area observation[J]. Acta Astronautica, 2020, 167: 93–107 [Google Scholar]
  27. ZHENG Minghui. Multi-star observation area coverage algorithm based on triangulation[D]. Changchun: Jilin University, 2023 (in Chinese) [Google Scholar]
  28. SONG Z, LIU H, DAI G, et al. Cell area-based method for analyzing the coverage capacity of satellite constellations[J]. International Journal of Aerospace Engineering, 2021(1): 6679107 [Google Scholar]

All Tables

表1

Dk所处状态的情况组合

In the text

All Figures

thumbnail 图1

对目标1的瞬时覆盖下球面三角形的状态
In the text
thumbnail 图2

对目标2瞬时覆盖下球面三角形的状态
In the text
thumbnail 图3

显示星座对目标1瞬时覆盖下, 通过算法3生成对所有未定状态的球面三角形的不确定性经
In the text
thumbnail 图4

目标2瞬时覆盖下球面三角形的不确定性经纬度框
In the text
thumbnail 图5

对目标1瞬时覆盖下的网格状态
In the text
thumbnail 图6

对目标2瞬时覆盖下的网格状态
In the text
thumbnail 图7

瞬时覆盖下κ值随着传感器覆盖圆半径的变化曲线
In the text
thumbnail 图8

对目标1的累积覆盖范围
In the text
thumbnail 图9

对目标2的累积覆盖范围
In the text
thumbnail 图10

累积覆盖下κ值随着覆盖圆半径变化的曲线
In the text
thumbnail 图11

对目标1的连续覆盖范围结果
In the text
thumbnail 图12

对目标2的连续覆盖范围结果
In the text
thumbnail 图13

连续覆盖下κ值随着覆盖圆半径变化的曲线
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.