EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 2 (April 2025) JNWPU, 43 2 (2025) 295-304 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 2, April 2025
Page(s) 295 - 304
DOI https://doi.org/10.1051/jnwpu/20254320295
Published online 04 June 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

四旋翼无人机(Quadrotor UAV)是一种通过电动马达驱动4个螺旋桨旋转产生的上升动力来实现垂直起降和稳定飞行的无人驾驶飞行器[1], 具备垂直起降、悬停等多种运动能力[1]。但也存在一些缺点, 作为六输出、四输入的强欠驱动系统[1–2]，抗扰性差，控制复杂。

针对Quadrotor UAV多输入、多输出、欠驱动、强耦合和高度非线性等特点[1–3], 学者们已提出许多先进控制算法对其进行控制, 如: PID控制[4]、滑模控制[5–6]、ADRC[7]、反步法[8]、自适应控制[9]、H∞控制[10]、神经网络控制[11]以及模糊控制[12]等。然而上述控制方法在处理多因素问题时均存在局限性。在实际系统算法设计过程中, 应综合考虑各种算法的优缺点，进行组合设计来实现控制。

在实际系统中, 广泛存在的外部扰动严重危及系统性能, 因此亟需有效的抗扰方法。文献[13–15]针对存在外部干扰的Quadrotor UAV非线性系统进行研究。文献[16–19]在上述研究外部干扰的基础上, 加入不确定性进行研究, 其中：文献[16]提出了一种有限时间扩张观测器的非奇异积分滑模姿态控制策略, 实现了对Quadrotor UAV姿态在有限时间内的跟踪控制; 文献[17]采用分层控制策略, 基于干扰观测器设计自适应非奇异终端滑模控制器，处理干扰以及参数不确定性, 实现对Quadrotor UAV系统的稳定控制; 文献[18]采用神经网络与滑模控制相结合设计自适应鲁棒控制器, 实现了在综合扰动下对Quadrotor UAV系统的轨迹跟踪控制; 文献[19]针对存在输入饱和、模型不确定性和外部扰动的Quadrotor UAV系统, 采用带有参数调整机制的双曲切线函数构造非对称饱和非线性逼近器, 结合神经网络、反步法, 设计了抗饱和有限时间控制器, 实现对Quadrotor UAV系统的鲁棒稳定控制。

系统的输入饱和、外部干扰、模型不确定性以及有限时间控制是设计Quadrotor UAV控制器时需要考虑的常见因素。对于输入饱和, 由于物理条件的限制, 执行机构的输出幅值是有限的, 若不加以处理可能导致整个控制系统失控。文献[20–21]均是针对Quadrotor UAV存在外部干扰和输入饱和的跟踪控制问题进行研究的。文献[22]针对Quadrotor UAV系统惯性参数不确定的轨迹跟踪问题, 采用分层控制、饱和命令控制以及投影算法相结合的策略, 设计了一种新的浸入式不变性自适应控制器, 实现Quadrotor UAV系统的质量估计渐近收敛于其真实值以及系统输出渐近地跟踪参考轨迹。文献[23]是在文献[22]研究参数不确定性的基础上加入位置约束进行研究, 同时结合动态面技术设计鲁棒控制器实现对Quadrotor UAV的稳定控制。然而目前关于Quadrotor UAV文献研究多集中于单一或两个因素(如干扰、输入饱和、不确定性、有限时间控制), 全面考虑多种因素的研究更有意义尚需深入。

基于此, 考虑Quadrotor UAV在飞行过程中同时存在输入饱和、外部干扰、系统不确定性以及有限时间多因素控制问题, 本文提出了一种同时抗扰、抗饱和、补偿系统不确定性的有限时间鲁棒控制方法。本文的创新点在于: 在Quadrotor UAV系统引入输入饱和和系统不确定性以及外部干扰, 针对系统输入饱和采用辅助系统去处理, 针对系统外部扰动采用非线性干扰观测器对其进行估计, 针对系统不确定性采用神经网络去逼近。最终, 基于Lyapunov有限时间稳定性理论在反步法框架下设计了系统的有限时间控制器, 并证明整个闭环系统的误差信号有界且收敛, 整个闭环系统在有限时间稳定。

1 系统描述和问题说明

1.1 四旋翼无人机系统建模

四旋翼无人机的坐标系结构示意图如图 1, 其中EI={OI, XI, YI, ZI}为地面惯性坐标系, 坐标系原点OI, Eb={Ob, Xb, Yb, Zb}为机体坐标系, 坐标系原点Ob位于Quadrotor UAV的机体重心处。根据牛顿欧拉动力学可得Quadrotor UAV的动力学模型[21]如(1)式所示。

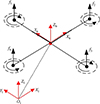thumbnail 图1

四旋翼无人机的坐标系示意图

式中：ξ=[x, y, z]T和β=[u v w]T分别为Quadrotor UAV系统在惯性坐标系下的位置向量和速度向量。η=[φ, θ, ψ]T和Ω=[p, q, r]T分别为Quadrotor UAV系统在机体坐标系下的姿态角向量和姿态角速度向量。ε=[0,0,1]T, g为重力加速度, ut为旋翼的总升力。Rbeε/m=R=[Rx Ry Rz]T, Reb表示从机体坐标系到惯性坐标系的转换矩阵, Σ=[u2, u3, u4]T, Σ表示Quadrotor UAV的力矩控制输入, Rbeεut/m=[u1x u1y u1z]T=Ut, u1=ut, L=diag(l, l, 1), J=diag(Jx, Jy, Jz)为x, y, z轴转动惯量构成的矩阵, l为旋翼中心与机身重心间的有效距离, Δ(ξ)和Δ(η)分别为系统位置环和姿态环的未建模动态以及不确定性, Dt和Dτ分别为位置环和姿态环的外力干扰和外部力矩干扰。

1.2 控制目标

本文控制目标是设计抗饱和且抗干扰的有限时间控制器，保证Quadrotor UAV在系统建模不确定情况下实现稳定地跟踪期望参考信号。在后续控制器设计过程中, 以下假设和引理将作为重要基础。

假设1 [19]   系统外部干扰Dt和Dτ是有界的, 且满足‖Di‖≤σi, (i=t, τ), σi为正常数。

假设2 [19]   参考轨迹xd=[ξd, ηd]及其一阶导数 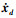和二阶导数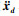均为连续且有界, 即存在已知正数 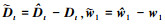成立, 其中Ea为一紧集, rr>0。

假设3    Δ(ξ)和Δ(η)是未知有界光滑函数, 并且其一阶导数和二阶导数均为有界的。

假设4    在飞行过程中, Quadrotor UAV的滚转角和俯仰角均在-90°~90°之间合理变化。

引理1 [18–19]   作为一种通用逼近器, 径向基神经网络经常被用来逼近任意未知连续函数, 其具体形式为

式中：H(Za)为未知连续函数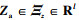；为神经网络的输入向量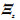；为状态向量允许的紧集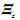；和 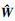分别为最优权值矩阵W*和未知函数H(Za)的估计值。

其中S(Za)=[S1(Za), S2(Za), …, Sj(Za)]∈Rj为基函数向量, 其元素一般具有如下结构

式中：i=1, 2, …j。hi∈Rl和λai∈R分别为基函数的中心和宽度, 可以看出, 如果选取足够多的节点数, 定义在紧集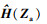上的任意连续函数H(Za)均能被逼近出来。H(Za)的形式为

式中, ‖ε*‖≤εN为逼近误差, εN>0为正常数。

引理2 [24]   考虑Quadrotor UAV系统模型(1)式, 如存在光滑正定函数 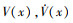≤-haVκ(x)+ hb成立, 其中, ha>0, 0 < κ < 1, 0 < hb < ∞为实数, 则Quadrotor UAV的轨迹是有限时间稳定的, 稳定时间Tst可由下式求出。

式中，0 < da < 1为常数。

引理3 [22]   对任意实数 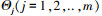, 下面的不等式成立

式中，0.5 < Va < 1, 0 < la < 2。

引理4 [22]   对于任意的正常数sa1, sa2和sa3, 如下的不等式成立

式中，τa1和τa2为实变量。

2 控制器设计和稳定性分析

2.1 位置环控制器设计

模型(1)中定义位置环的跟踪误差为

式中: α1为虚拟控制量; λ1和λ2为辅助系统的状态变量; ξd为期望的位置。

辅助系统设计为

式中: c1=c1T和c2=c2T是需要构造的正定对角矩阵, 以下等式中sat(·)为饱和函数, utmax为ut的最大值。

位置环的虚拟控制律

式中，k1=k1T>0为需要构造的正定对角矩阵; 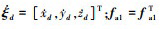为需要构造的正定对角矩阵, fa1=diag[fa11, fa12, fa13], fa1i>0, i=1, 2, 3;Va是一个实常数, 满足0.5 < Va < 1。

根据引理1, 系统位置环的不确定性L1Δ(ξ)=w1Th1+ε1, 估计值 。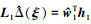

为了处理系统位置环的外部干扰, 设计以下非线性干扰观测器

式中: L1=L1T为需要构造的正定对角矩阵; 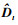为Dt的估计。

位置环控制输入Ua及神经网络权重更新律分别设计如下

式中：Λ为需要构造的正定对角矩阵；c2= c2T>0为需要构造的正定对角矩阵；ρ1>0为常数。fb1=diag[fb11, fb12, fb13]为需要构造的正定对角矩阵, fb1i>0, i=1, 2, 3。

2.2 姿态环控制器设计

模型(1)中定义姿态环的跟踪误差为

式中: α2为虚拟控制量；λ3和λ4为辅助系统的状态变量；ηd为期望的姿态角向量。

辅助系统设计为

式中: p1=p1T和p2=p2T是需要构造的正定对角矩阵。以下等式中sat(·)为饱和函数。uτmax为uτ的最大值。

姿态环的虚拟控制律

式中：m1=m1T>0为需要构造正定对角矩阵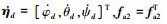；为需要构造的正定对角矩阵, fa2=diag[fa21, fa22, fa23]，fa2i>0, i=1, 2, 3。

根据引理1, 系统姿态环的不确定性L2Δ(η)=w2Th2+ε2, 估计值 。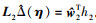

为了处理系统姿态环的外部干扰, 设计以下非线性干扰观测器

式中：L2=L2T为需要构造的正定对角矩阵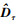；为Dτ的估计。

姿态环控制输入Ub及神经网络权重更新律分别设计如下

式中: 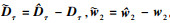为需要构造的正定阵; m2=m2T>0为需要构造的正定对角矩阵; ρ2>0为常数。fb2=diag[fb21, fb22, fb23]为需要构造的正定对角矩阵, fb2i>0, i=1, 2, 3。

2.3 稳定性分析

定理1   对于Quadrotor UAV飞行系统(1)以及假设1, 2, 3, 4, 选择辅助系统(4)和(10), 虚拟控制信号(5)和(11), 控制输入信号(7)和(13), 以及神经网络权重更新律(8)和(14), 则闭环系统的所有误差信号在有限时间有界且稳定。

首先对位置环的稳定性进行分析证明。

定义如下Lyapunov函数

式中，。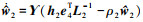

对(15)式V1求导并代入(3)~(6)式得

根据Young不等式

将参数更新律(8)式代入上式, 其中

根据Young不等式得

整理得

下面对姿态环的稳定性进行分析。

定义如下Lyapunov函数

式中，。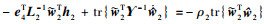

对(17)式V2求导并代入(9)~(12)式得

根据Young不等式

整理得:

将更新律 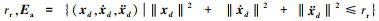代入上式, 其中 。

根据Young不等式得

整理得

最后对闭环系统进行稳定性分析证明。

选取包含位置环和姿态环的Quadrotor UAV整体系统备选Lyapunov函数如下

对(19)式求导并代入(16)式和(18)式得

根据引理3得到

式中，fa1m=min{fa1i}, fa2m=min{fa2i}, fb1m=min{fb1i}, fb2m=min{fb2i}。

将(23)~(26)代入(20)式得

根据引理4, 令τa1=V3, τa2=1, sa1=Va, sa2=1-Va, sa3= 1 Va, 可得

结合(28)式、(27)式可进一步写为

式中：κ3=min{κ1, 2Vafa1m, 2Vafb1m, 2Vafa2m, 2Vafb2m}, 。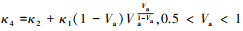

定义稳定时间

将(30)式在[0, t]积分可得

根据V3的定义可知

跟踪误差e1最终一致有界, 同理, 闭环系统中的其他误差信号也均最终一致有界。由(3)式知ξ-ξd=e1+ λ1有界, 同理由(9)式知η-ηd=e3+ λ3有界, 即闭环系统的跟踪误差均收敛至原点附近的一个较小邻域内。

为保障闭环系统的稳定性, 选择的设计参数应满足以下条件

闭环系统有限时间稳定性分析证明完毕。

由(7)式所示位置环的控制输入Ua可得: Ua=[u1x, u1y, u1z]T, 通过(32)~(34)式可得系统期望的俯仰角θd和横滚角φd和总升力u1。

3 仿真与分析

3.1 仿真参数设置

本节利用simulink仿真技术对所设计的控制器性能进行验证。

参考位置信号为ξd=[sint, cost, -0.3t]T, 偏航角ψd=60°Quadrotor UAV的初始位置和初始姿态角分别设置为ξ0=[2,1,0]T, η0=[0,0,0]T, Quadrotor UAV系统参数为m=0.8 kg, g=9.8 m2/s, Jx=0.015 67 kg·m2, Jy=0.015 67 kg·m2, Jz=0.015 67 kg·m2, 转动惯量所构成矩阵为J=diag{Jx, Jy, Jz}。

控制器参数设计为: c1=diag{5, 5, 5}, c2=diag{5, 5, 5}, k1=diag{2, 3, 1.3}, k2=diag{4, 3, 4}, p1=diag{5, 5, 5}, Va=0.9, p2=diag{5, 5, 5}, m1=diag{20, 20, 20}, m2=diag{30, 30, 30}, Λ= I3×3, γ = I3×3。L1={5, 5, 5}, L2={30, 30, 30}, ρ1=0.5, ρ2=0.5, fa1= I3×3, fa2= I3×3, fb1= I3×3, fb2= I3×3。

位置环与姿态环干扰值

位置环与姿态环不确定性为

3.2 仿真结果

分析1   图 2~7表示文献[4]所提出PID控制、文献[25]所提出的滑模控制以及本文所设计的控制器对Quadrotor UAV系统控制的轨迹跟踪结果对比图。从图 2~7可见, 在轨迹跟踪过程中, PID控制在控制系统稳定前是超调量最大或调节稳定时间最长的, 在z轴方向轨迹和偏航角跟踪过程中存在稳态误差, 滑模控制跟踪效果比PID效果好, 但存在明显的震荡现象, 在z轴方向轨迹和偏航角跟踪过程中也存在稳态误差。以上3种控制方法均能在有外部干扰、输入饱和、系统不确定性存在的情况下跟踪上期望的参考信号, 但是本文所设计的控制器在系统中的控制效果是最好的, 跟踪误差最小、跟踪速度快且超调量较小。

thumbnail 图2

x轴方向跟踪结果对比

thumbnail 图3

y轴方向跟踪结果对比

thumbnail 图4

z轴方向跟踪结果对比

thumbnail 图5

滚转角跟踪结果对比

thumbnail 图6

俯仰角跟踪结果对比

thumbnail 图7

偏航角跟踪结果对比

分析2   图 8~11为控制器输入曲线。图 12~13为位置环和姿态环外部干扰跟踪结果图。由图 8可以看出, 位置环总升力曲线在大于9 N之后被滤平, 保持在9 N, 图 9~11可以看出姿态环的输入力矩在大于8 N·m时, 保持在8 N·m, 系统的4个控制输入均是有界的。从图 12和图 13显见, 所设计的非线性干扰观测器具有较好的跟踪外部干扰的性能。从系统整体的控制效果看, 所设计的控制器能够提高Quadrotor UAV的控制性能, 可以保证其安全飞行, 并且能在有效时间Tst内保障系统稳定。

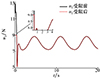thumbnail 图8

控制输入曲线u1

thumbnail 图9

控制输入曲线u2

thumbnail 图10

控制输入曲线u3

thumbnail 图11

控制输入曲线u4

thumbnail 图12

位置环干扰跟踪结果

thumbnail 图13

姿态环干扰跟踪结果

3.3 仿真结果总结

通过仿真结果可知: PID控制算法可以控制存在外部干扰、系统不确定性以及输入饱和情况下的Quadrotor UAV系统, 但是超调量较大以及稳定时间较长, 在控制器设计中, 控制设计参数较大并且控制结果存在一定的稳态误差。滑模控制方法在处理系统存在不确定性以及外部干扰时, 需要设计较大的切换增益, 控制效果才能够优良, 但会导致较大的振颤现象。从以上的仿真图中可以看出，滑模控制不管是在位置环或者姿态环控制过程中, 均存在明显的震颤且有一定的超调量。而本文所设计的有限时间控制器不管是在稳态性能还是在瞬态性能方面控制效果最好, 跟踪快、稳态误差小, 具有较强的抗输入饱和能力和鲁棒性, 能够保证Quadrotor UAV的飞行性能要求。

4 结论

针对Quadrotor UAV存在外部干扰、系统不确定性、输入饱和的情况, 本文采用神经网络逼近系统的不确定性, 采用辅助系统处理系统的输入饱和, 采用非线性干扰观测器估计系统的外部干扰, 最终在反步法的框架下, 设计了基于有限时间的鲁棒控制器。仿真实验结果显示依据所设计的控制器可以在有限时间Tst内有效处理系统模型的不确定性和外部干扰以及输入饱和, 有较强的处理饱和能力和鲁棒性, 总结如下:

1) 本文提出的控制方法性能优于传统的PID控制和滑模控制方法, 有效地提高了系统的抗扰和抗饱和性能。

2) 所设计的神经网络能够实时地逼近系统的不确定性; 非线性干扰观测器能够实时地估计出系统的外部干扰值; 结合逼近值、估计值和辅助系统设计有限时间的控制器, 可有效增强Quadrotor UAV飞行抗饱和能力以及鲁棒性。

3) Quadrotor UAV系统在控制器的作用下可实现有限时间Tst内所有误差信号有界稳定。

考虑Quadrotor UAV在实际空中飞行环境的复杂性, 不仅可能发生输入饱和, 还可能发生输出受限以及状态约束等问题, 这将是下一步工作研究的方向。

References

  1. ZHOU Laihong. Research on robust and fault-tolerant control of quadrotor[D]. Shenyang: Northeast University, 2019 (in Chinese) [Google Scholar]
  2. LU Hongzhi, DUAN Fuhai. Research on fault-tolerant control of altitude and attitude for quadcopter drones[J]. Electronics Optics & Control, 2023, 30(12): 73–79 (in Chinese) [Google Scholar]
  3. SUN Guhao, ZENG Qingshuang. Secure trajectory tracking control of quadcopter unmanned aerial vehicles[J]. Control Theory & Applications, 2023, 40(7): 1261–1269 (in Chinese) [Google Scholar]
  4. PENG Cheng, BAI Yue, QIAO Guanyu, et al. Yaw anti-saturation and multi-mode PID control of quadrotor unmanned aerial vehicle(UAV)[J]. Robot, 2015, 37(4): 415–423 (in Chinese) [Google Scholar]
  5. LI Yonggang, LI Xingye. Adaptive sliding mode control for nonlinear systems subject to saturated input constraints[J]. Computer Engineering and Applications, 2010, 46(31): 235–238 (in Chinese) [Google Scholar]
  6. FU Mingyu, WANG Shasha, WANG Yuanhui, et al. Adaptive sliding mode control of underactuated surface ship parameters with input saturation[J]. Journal of Harbin Engineering University, 2019, 40(1): 202–209 (in Chinese) [Google Scholar]
  7. YANG Liben, ZHANG Weiguo, HUANG Degang. Robust trajectory tracking of a quadrotor based on ADRC attitude decoupling[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(6): 1026–1032 (in Chinese) [Google Scholar]
  8. ZHANG Juqian, REN Chaohui, ZHOU Laihong. Robust and adaptive flight control of quadrotor based on exponential convergence[J]. Journal of Chinese Inertial Technology, 2016, 24(4): 548–553 (in Chinese) [Google Scholar]
  9. MOU C. Adaptive neural control of uncertain nonlinear systems using disturbance observer[J]. IEEE Trans on Cybernetics, 2017, 47(10): 3110–3123 [Article] [Google Scholar]
  10. LI Meng, SHI Yong. Design and Implementation of robust H∞ UAV flight control system[J]. The Journal of Beijing Institute of Technology, 2016, 36(8): 807–812 (in Chinese) [Google Scholar]
  11. MA J, XU S Y, ZHUANG G M, et al. Adaptive neural network tracking control for uncertain nonlinear systems with input delay and saturation[J]. International Journal of Robust and Nonlinear Control, 2020, 30(7): 2593–2610 [Article] [Google Scholar]
  12. WU C, LIU J, JING X. Adaptive fuzzy control for nonlinear networked control systems[J]. IEEE Transa on Systems, Man, and Cybernetics, 2017, 47(8): 2420–2430 [Article] [Google Scholar]
  13. CHEN Yanmin, HE Yongling. Distributed PID neural network control for quadcopter[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 185–190 (in Chinese) [Google Scholar]
  14. HERIBERTO R. Robust backstepping control based on integral sliding modes for tracking of quadrotors[J]. Journal of Intelligent & Robotic Systems, 2014, 73(1/2/3/4): 51–56 [Google Scholar]
  15. ZHENG E. Sencond order sliding mode control for a quadrotor UAV[J]. Original Research Article ISA Transactions, 2014, 53(4): 1350–1356 [Google Scholar]
  16. ZHU Wenxing, WANG Lihui, TIAN Bailing. Integral sliding mode control method for quadrotor unmanned aerial vehicles based on finite-time observe[J]. Journal of Chinese Inertial Technology, 2023, 31(12): 1244–1253 (in Chinese) [Google Scholar]
  17. LI Z, MA X, LI Y B. Robust trajectory tracking control for a quadrotor subject to disturbances and model uncertainties[J]. International Journal of Systems Science, 2020, 51(5): 839–851 [Google Scholar]
  18. HADI R, SIMA A. Neural network-based adaptive sliding mode control design for position and attitude control of a quadrotor UAV[J]. Aerospace Science and Technology, 2019, 91: 12–27 [Google Scholar]
  19. XU Q Z, WANG Z S, ZHEN Z Y. Adaptive neural network finite time control for quadrotor UAV with unknown input saturation[J]. Nonlinear Dynamics, 2019, 98(3): 1973–1998 [Google Scholar]
  20. LIU K, WANG X X, WANG R J., et al. Antisaturation finite-time attitude tracking control based observer for a quadrotor[J]. IEEE Trans on Circuits and Systems, 2021, 68(6): 2047–2051 [Google Scholar]
  21. LIU K F, WANG R. Antisaturation command filtered backstepping control based disturbance rejection for a quadrotor UAV[J]. IEEE Trans on Circuits and SystemsⅡ: Express Briefs, 2021, 68(12): 3577–3581 [Google Scholar]
  22. ZHOU Y, ZHU B. Adaptive trajectory tracking controller for quadrotor systems subject to parametric uncertainties[J]. Journal of the Franklin Institute, 2017, 354(15): 6724–6746 [Google Scholar]
  23. SHAO X L, WANG L W, LI J. High-order ESO based output feedback dynamic surface control for quadrotors under position constraints and uncertainties[J]. Aerospace Science and Technology, 2019, 89288–298 [Google Scholar]
  24. WANG F, ZHANG X. Adaptive finite time control of nonlinear systems under time-varying actuator failures[J]. IEEE Trans on Systems, Man and Cybernetics: Systems, 2019, 49(9): 1845–1852 [Google Scholar]
  25. WANG L, LI G C, WANG Z L, et al. Sliding mode control of an underactuated quadrotor UAV[J]. Journal of Harbin Engineering University, 2012, 33(10): 1248–1253 [Google Scholar]

All Figures

thumbnail 图1

四旋翼无人机的坐标系示意图
In the text
thumbnail 图2

x轴方向跟踪结果对比
In the text
thumbnail 图3

y轴方向跟踪结果对比
In the text
thumbnail 图4

z轴方向跟踪结果对比
In the text
thumbnail 图5

滚转角跟踪结果对比
In the text
thumbnail 图6

俯仰角跟踪结果对比
In the text
thumbnail 图7

偏航角跟踪结果对比
In the text
thumbnail 图8

控制输入曲线u1
In the text
thumbnail 图9

控制输入曲线u2
In the text
thumbnail 图10

控制输入曲线u3
In the text
thumbnail 图11

控制输入曲线u4
In the text
thumbnail 图12

位置环干扰跟踪结果
In the text
thumbnail 图13

姿态环干扰跟踪结果
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.