EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 2 (April 2025) JNWPU, 43 2 (2025) 398-409 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 2, April 2025
Page(s) 398 - 409
DOI https://doi.org/10.1051/jnwpu/20254320398
Published online 04 June 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

外辐射源雷达是一种新体制雷达, 通过接收目标反射的第三方辐射源的电磁波对目标进行定位, 具有覆盖范围广、全天时全天候等优势。随着北斗卫星导航系统的不断完善，出于战时安全性考虑, 基于北斗卫星外辐射源的雷达系统近年来备受关注。外辐射源信号经过目标散射后能量微弱, 需要通过较长时间的积累来完成对高速目标的有效检测。在以北斗卫星为辐射源的探测场景中, 高机动微弱目标的复杂运动状态会导致其回波跨越多个距离-多普勒分辨单元, 造成能量分散, 难以进行有效积累[1]。同时, 由于目标本身的散射能量微弱, 加之电磁环境的复杂多变, 目标散射特性易发生显著变化, 在这些因素共同作用下, 难以保证长时间积累过程中目标回波信号的相干性, 进而降低了对这类目标的检测性能[2]。

长时间积累技术可以分为非相参积累、相参积累和混合积累三类。在相同的积累时间内相参积累在积累效率上最优, 但运算复杂度较高。非相参积累在运算量和实施方面优势较大, 但积累性能较差[3]。为平衡运算量和检测性能, 混合积累方法被提出。文献[4]针对高速弱目标提出了一种高速弱目标检测的帧内和帧间联合积累方法, 对高速匀速目标的多帧信号进行处理, 利用Radon-Fourier变换(RFT)对每帧内的目标信号进行积累, 并通过动态规划算法(DP)对多帧RFT积累结果进行处理, 有效地实现了帧间RFT峰值能量的积累。但该算法仅适用于匀速运动目标, 且运算复杂度较高。文献[5]采用分段处理的思想, 提出了一种基于马尔可夫运动模型的高机动雷达目标检测混合积累方法。采用RFT、DP和二元积累(BI)进行混合积累, 具有良好的检测和积累性能, 但同样只适用于匀速运动目标, 对复杂高机动运动目标的检测效果不理想。文献[6]提出了基于小波去噪的一阶线性补偿与DP相结合的目标回波长时间混合积累算法。根据机动目标的运动参数划定子段长度, 满足子段内不发生跨距离单元徙动和最大加加速度带来的跨多普勒单元徙动不超过多普勒分辨率一半的条件。这种分段方法受目标运动参数最大值的限制, 存在局限性。文献[7]提出了一种天基无源雷达系统的运动目标检测技术, 将Keystone变换和分数阶傅里叶变换(FrFT)应用在连续的短时间间隔内, 然后在多个帧FrFT变换结果的质心执行非相干积累, 实现运动目标的检测。

以卫星为外辐射源, 针对复杂高机动弱小目标的运动状态不稳定, 长时间积累相干性无法保证的问题, 本文提出了一种基于非均匀子孔径划分的外辐射源雷达高机动弱小目标混合积累算法。本文所提方法结合广义二分法(generalized bisection method, GBM)对整个积累时间内的目标回波信号进行非均匀有效划分, 确保目标信号能够在单个子孔径内聚集到同一距离单元。采用FrFT算法估计目标在子孔径内的运动参数, 对目标信号进行跨多普勒单元徙动补偿, 实现子孔径内目标回波信号的有效相参积累。最后, 采用DP算法对多个子孔径的相参积累结果进行非相参积累, 完成对目标能量的有效积累。所提GBM-FrFT-DP算法可以有效解决长时间积累情况下受到系统自身误差、环境影响、目标反转运动、空间传输等因素的影响, 高机动目标信号相参性会大大下降的问题, 实现对高机动微弱目标的有效探测, 降低运算复杂度。

此外, 本文对所提算法进行了仿真实验, 验证了方法的可行性。所提算法能够实现高机动微弱目标能量的有效积累。

1 信号模型

外辐射源雷达一般包含参考天线和回波天线2套天线系统, 参考天线用来接收辐射源的直达波信号, 回波天线用来接收目标的反射波信号。假设参考通道中除噪声外, 无其余干扰信号。

不失一般性, 本文假设卫星外辐射源发射的信号时域表达式为

式中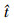：为时间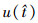；为信号的复包络；fc为载频。

对直达波进行录取, 可得参考通道中的直达波信号为

式中：t为快时间；tm为慢时间；Ar为参考通道中直达波的复幅度；c是光速；Rb(tm) 表示外辐射源与地面接收站的直达距离。

对反射波进行录取, 可得回波通道中的反射波信号为

式中：Ae为回波通道中反射波的复幅度；Rt(tm)表示目标在观测时间内与外辐射源的距离；Rr(tm) 表示目标在观测时间内与地面接收站的距离。

对参考通道信号和回波通道信号进行去载波和相关处理, 经直达波抑制[8–10]与多径抑制[11–12]处理后, 可得信号为

式中：A1为脉压后的回波复幅度；B为带宽；R(tm)表示雷达在观测时间内与目标之间的等效径向距离, 它是慢时间tm的函数, 可表示为

式中：R0=Rt(0)+Rr(0)-Rb(0)表示目标等效初始距离；v为目标的等效径向速度；a为目标的等效径向加速度, 可表示为

式中：a0为起始等效加速度；Δa∈[-Δam, Δam]为多种影响因素造成的加速度随机量；a′max为段内等效最大加加速度；Tseg=Tmin+ΔT为非均匀时间段。

将等效径向距离R(tm) 代入信号表达式可得

从(8)式中看出, 高机动目标由于速度v和加速度a的存在, 长时间积累会导致目标回波信号能量产生跨距离单元徙动和跨多普勒单元徙动的问题, 降低微弱目标的积累性能。

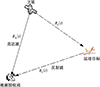thumbnail 图1

外辐射源雷达系统模型

2 基于非均匀子孔径划分的外辐射源雷达高机动微弱目标混合积累算法

针对长积累时间内高机动微弱目标无法保证相参性及运算复杂度大幅提升的问题, 基于非均匀子孔径划分的外辐射源雷达高机动微弱目标混合积累算法相比于现有的均匀子孔径划分混合积累算法更符合复杂高机动微弱目标的运动状态。通过非均匀子孔径有效划分保证了子孔径内目标回波信号不发生跨距离单元徙动, 对子孔径内目标信号进行相参处理, 子孔径之间对目标信号进行非相参处理。

2.1 非均匀子孔径划分

2.1.1 广义二分法划分原理

二分法, 也称为折半搜索, 是在有序数组中寻找某个特定元素最常用的算法之一。本文中, 采用广义二分法对整个积累时间进行划分。将整个积累时间看成一个完整的区间, 将其一分为二, 经过信号预处理后判断左右区间目标可能所在的距离单元是否一致。若不一致, 则继续将左右区间一分为二进行判断, 直到查找到目标可能所在距离单元一致的左右区间或者划分到最小区间数, 区间划分停止。划分处理示意图如图 2所示。

信号经过二分法划分之后被分为左右两部分, 区间内信号表达式为

式中：m∈[ml, mr], ml为区间起始脉冲序号；mr为区间结束脉冲序号。

假设总脉冲区间为[1, M], 则第一次划分结束后, 左脉冲区间为[1, round(1+(M-1)/2)], 右脉冲区间为[1+round(1+(M-1)/2), M], round表示将数值四舍五入到最接近的整数。对左右脉冲区间内的目标回波信号继续进行划分, 直到满足区间划分截止条件为止。记录满足条件的区间位置和区间大小。

thumbnail 图2

二分法处理示意图

2.1.2 区间划分截止条件

区间划分截止条件: 左右两区间内目标可能存在的距离单元唯一且位置相同或区间长度达到最小, 即认为目标在区间内不发生跨距离单元徙动现象, 停止划分。

最小区间长度: 对外辐射源雷达接收系统进行分析, 根据可探测范围内各部分信号处理的积累增益, 可得到理想状态下子孔径内的最短相参积累脉冲个数, 进而计算出满足非相参积累最小信噪比条件的最小区间长度。

信噪比是目标探测性能评价指标中的一个最重要的概念, 用信噪比的增强程度来衡量信号处理各部分的积累性能。

信噪比定义表达式为

式中：Ps为回波信号功率；Pn为噪声功率。

根据雷达方程可得, 回波信号可检测目标信号所需的最小输出信噪比为

式中：Pt为雷达发射功率；Gt为外辐射源雷达发射天线增益；PtGt为卫星外辐射源的有效发射功率；σ为目标雷达散射截面积；Gr为接收机天线增益；λ为发射信号波长；Rt为目标到卫星外辐射源的距离；Rr为目标到地面接收天线的距离；k为波尔兹曼常数；Ts为系统等效噪声温度；B为接收机带宽；L为雷达各部分的损耗。

假设脉冲压缩前目标回波信号的输入信噪比为RSN, in, 经过处理后目标回波信号的输出信噪比为RSN, out。

式中：GCIT为长时间相参积累的信噪比增益；GPC为脉冲压缩的信噪比增益；GDBF为数字波束形成增益；D为时宽带宽积[13]。

理想情况下, 均匀线阵数字波束形成处理信噪比增益与阵元数呈正比，如(14)式所示。

式中, N1为阵元个数。

理想情况下, N个脉冲相参积累的信噪比增益为

要求子孔径内相参积累结果输出目标信噪比最低门限为0 dB, 可以根据雷达系统参数计算各部分增益, 再结合(15)式计算出理想状态下子孔径内的最短相参积累脉冲个数N。

在机动弱目标不发生跨波束单元徙动的前提下, 长时间积累过程中目标仍会产生跨距离单元徙动和跨多普勒单元徙动现象, 子孔径划分也需要考虑机动目标径向运动带来的影响。

经过划分后左右区间内目标可能存在的距离单元唯一且位置相同, 可表示为

式中：vl/r为左/右区间内目标等效速度；al/r为左/右区间内目标等效加速度；tml=mlTr为区间起始时间；tmr=mrTr为区间结束时间。R0kiL为左区间内目标所在距离位置, R0kiR为右区间内目标所在距离位置。

区间长度达到最小, 可表示为

式中, Mmin为区间最小脉冲长度, 且Mmin≥N。

2.1.3 子孔径划分

对目标所在距离单元位置相同的相邻区间进行合并, 完成非均匀子孔径的划分。非均匀子孔径划分处理流程图如图 3所示。

由于弱小目标回波信号能量微弱, 回波信号中包含很多噪声, 为了更好地判断区间内目标信号所在距离单元位置, 对左右区间内的回波信号进行回波信号预处理与门限判决。

首先, 对两区间的回波信号做慢时间维FFT，完成区间内回波信号的相参积累, 提高目标信号的能量。对得到的相参积累结果进行“幅值和”分析与门限判决。得到左右区间内目标可能存在的距离单元位置, 处理流程如图 4所示。

1) 区间内信号处理

首先, 对区间内的回波信号进行慢时间维FFT, 完成区间内回波信号的相参积累, 得到

式中：Aki为区间内相参积累后的回波信号复幅度；R0ki表示区间内目标回波信号的等效距离；vki表示区间内目标回波信号的等效径向速度。

经过相参处理后, 目标能量得到了有效积累。但由于微弱目标的高机动性, 信号能量会随着速度vki和加速度aki的变化而发生扩散, 降低积累性能。对区间内回波信号的相参积累结果进行幅值和分析, 提取出每个距离单元回波信号对应的多普勒能量, 并进行非相参积累。积累能量值作为该距离单元的幅值和, 可得表达式为

对得到的幅值和进行门限检测, 选择出区间内目标可能存在的距离单元。

式中：ST=w·max|ski-sum(t)|为检测门限; w为门限选择对应权值。选出满足条件的距离单元R0ki为区间内目标可能存在的距离单元。

2) 区间合并

对完成非均匀划分的区间信号进行合并处理, 如图 5所示。将目标可能所在距离单元相同的区间信号进行合并, 在短时间内目标所处位置为同一距离单元, 可认为短时间内回波信号运动状态稳定, 能够保证目标回波信号相参性, 可以进行相参积累。

经过区间内回波信号预处理后, 若R0kiL=R0kiR, 认为相邻区间信号运动状态一致, 合并区间信号为子孔径信号, 保证子孔径内目标信号不发生跨距离单元徙动。将多个区间信号进行合并, 增加子孔径长度, 延长了子孔径内相参处理时间, 提高子孔径内目标相参积累性能, 提高弱目标检测性能。

经过区间合并处理后, 将整个回波信号非均匀地划分成K个子孔径, 目标回波信号可表示为

第k个子孔径内的回波信号表达式为

式中：tmk=mkTr, 每个子孔径的脉冲总数为Mk=mrk-mlk+1, mk∈[mlk, mrk]为每个子孔径内的脉冲序号。A1k为第k个子孔径内的目标回波信号复幅度, R0k为第k个子孔径信号所在的距离位置, vk为第k个子孔径信号的等效径向速度, ak为第k个子孔径信号的等效径向加速度。

分段后第k(k∈[1, 2, …, K]) 个子孔径的瞬时径向距离、瞬时径向速度以及瞬时径向加速度可以分别表示为

式中, R0k, vk, ak分别为每个孔径内回波信号的等效距离, 等效初始速度和等效中心加速度。

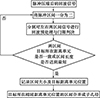thumbnail 图3

子孔径划分流程图
thumbnail 图4

区间内信号处理流程图
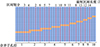thumbnail 图5

区间划分示意图

2.2 子孔径内信号跨多普勒单元徙动补偿校正

在2.1节中对回波信号进行了有效非均匀划分, 子孔径内的目标回波信号集中在同一距离单元。取每个子孔径内目标所在距离单元信号进行FrFT[14], 可得

当cotα=ak/λ并且ucscα=-vk/λ时, 信号在u-vk二维平面上出现峰值, 同时可以估计出目标的径向速度 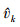和径向加速度 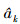。根据估计的目标运动参数构造补偿函数。

对子孔径内目标回波信号进行校正补偿。

当 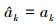时, 多普勒频率 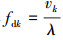, 目标信号能量聚集到此多普勒通道, 完成子孔径内目标信号跨多普勒单元徙动的补偿。

对完成跨多普勒单元徙动补偿的目标回波信号进行慢时间维指定点数的FFT, 进行子孔径内目标回波信号的相参积累。

式中：A2k为子孔径内目标信号相参积累后的复幅度；fdk为第k个子孔径目标信号的多普勒频率；δ(·)表示冲击函数。慢时间维FFT的点数为最大非均匀子孔径长度Mmax, 保证多个子孔径内的相参积累结果维度统一。

由于目标回波信号微弱, 必须采用长时间积累, 但目标运动状态复杂以及存在随机相位噪声等环境影响因素[2], 回波数据并不满足长时间相参积累条件, 故在子孔径间采用非相参积累算法。

2.3 子孔径间非相参积累

获得每个子孔径的相参处理结果sk=skhf(t, fdk)之后, 在积累时间内对所有子孔径处理结果进行非相参积累。

采用DP算法[15]对运动目标在K个子孔径内的相参积累结果进行非相参积累处理。将K个子孔径内运动目标的状态序列定义为: X1:K={x1, x2, …, xK}, 观测数据平面为t-fm二维平面, 每个平面内为N×M个分辨单元。S1:K={s1, s2, …, sK}为信号在K个子孔径的量测数据序列, sk={sij(k)}为第k个子孔径的量测值, 可表示为N×M的矩阵, sij(k)为第k个子孔径内的分辨单元(i, j) 的量测值, 可表示为

根据给定的量测数据序列, 通过DP算法最优化状态转移找到最符合真实目标的状态序列X1:K, 得到K个子孔径的非相参积累结果IK。

DP算法具体步骤为:

步骤1  初始化。对于第一个子孔径k=1, 对于状态X1有

式中：IX1为初始状态的值函数；ψXk(·)为在子孔径之间的动态规划DP回溯的索引函数。

步骤2  递归。当2≤k≤K(总时间为K)时, 对于k时刻的所有状态Xk

式中，τk(i, j)表示目标的状态转移范围。Xk-1是可以转移到Xk的可能状态。

步骤3  门限检测。当迭代结束时, 得到K个子孔径全部积累得到的值函数IXK, 找到值函数超过门限的状态。

式中：VT=w·max|IXK|为设定的检测门限; w为门限权值。若最后一个子孔径的积累结果能正常超过检测门限, 则最终得到了目标的积累结果IXK。

步骤4   回溯轨迹。当积累结果超过目标检测门限VT时, 对目标状态轨迹进行回溯, 可表示为

根据回溯结果, 可以得到目标在多个子孔径内的状态估计序列 。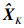

在进行目标检测性能分析前, 给出GBM-FrFT-DP混合积累算法中目标的检测概率与虚警概率。

目标检测概率(Pd)是指经过动态规划非相参积累处理后, 估计出的目标状态位置与真实状态位置的差不超过2个分辨单元, 同时, 积累值函数超过门限VT的概率。检测概率公式为

式中：xK为目标状态。

虚警概率(Pfa) 是指经过经过动态规划非相参积累处理、门限检测后, 存在不与目标相关联的噪声状态的概率。虚警概率的计算公式为

式中, yK为噪声状态。

2.4 GBM-FrFT-DP算法的处理流程

GBM-FrFT-DP算法的处理流程如图 6所示。

具体实现步骤为:

步骤1  对接收到的目标回波信号和直达波信号进行预处理, 得到脉冲压缩后的信号s(t, tm)。

步骤2  计算区间内最小脉冲数Mmin。

步骤3   进行有效非均匀区间划分。保证区间内运动目标不发生距离徙动现象。

步骤4   区间合并。将目标所在一个距离单元的区间进行合并, 完成子孔径的划分。

步骤5   子孔径内跨多普勒单元补偿。对子孔径内的回波信号, 进行FrFT操作, 估计出子孔径内目标回波信号的运动参数, 构造补偿函数H(tm), 完成目标回波信号跨多普勒单元徙动的补偿。

步骤6   对补偿之后的回波信号进行统一尺度的慢时间维傅里叶变换, 完成子孔径内信号的相参积累, 处理结果为skhf(t, fdk)。

步骤7   对多个子孔径回波信号处理之后的结果S1:K进行DP操作, 获得每个子孔径的动态规划处理结果IXk。

步骤8   根据检测到的目标状态进行过滤, 最终确定目标位置, 完成目标能量的积累。

thumbnail 图6

算法处理流程图

3 仿真实验及性能分析

本节通过仿真实验验证了GBM-FrFT-DP算法的有效性。

仿真参数如表 1所示。

对接收到的回波信号进行脉冲压缩，结果如图 7所示。

由图 7可以看出, 经过脉冲压缩之后的回波信号发生跨距离单元徙动且能量微弱, 无法有效观测出目标。在外辐射源雷达系统下, 根据雷达系统参数计算各部分增益, 结合公式(18)可以得到最小区间的脉冲个数为Mmin=32。

根据广义二分法对回波信号进行预处理, 完成广义二分法非均匀子孔径划分操作, 将信号有效划分为K个子孔径。区间划分结果如表 2所示, 子孔径合并结果如表 3所示。

由表 2区间划分结果可以看出区间划分长度是变化的, 可以推断出机动目标的速度随着加速度变化, 且由区间长度不一致反映出机动目标的速度变化存在随机性, 是由加速度的非均匀随机量导致的。由表 3可见, 通过对整个积累时间的有效非均匀划分, 已经将回波信号有效划分为7个长度不一致的子孔径信号。分别对子孔径内的信号进行多普勒补偿, 进行子孔径内目标回波信号的相参积累, 结果如图 8所示。

由图 8可见, 7个子孔径内的目标信号均被有效校正了跨多普勒单元徙动, 目标能量均集中在一个峰值单元内, 完成了7个子孔径内的目标回波信号的有效积累。从7个子孔径信号的相参积累结果峰值位置可以看出, 由于目标的机动性, 目标峰值位置在7个子孔径间存在偏移, 且不是线性变化。

依次对K个子孔径的相参积累结果进行DP非相参积累, 结果如图 9所示。由图 9及表 4可以看出, GBM-FrFT-DP算法可以在长积累时间内目标信号相参性无法保证的条件下对复杂高机动微弱目标能量进行有效积累。目标位置在第74个距离单元, 多普勒频率为-240Hz, 与最后一个子孔径目标运动状态匹配, 与目标真实状态更接近。目标积累能量值大致为7个子孔径内目标相参积累能量幅值之和。DP算法对7个子孔径内的目标信号相参积累结果进行最优化搜索, 得到目标在7个子孔径间的状态转移轨迹, 如图 10所示。DP算法能够在子孔径间对目标能量进行有效非相参积累。

在无法保证长时间积累相参性的条件下, 针对复杂机动微弱目标, 均匀分段KT-FrFT质心对齐混合积累算法对目标的积累效果不明显, 目标能量仍然有明显扩散, 处理结果如图 11所示。而传统相参积累算法在保证长时间积累相参性的条件下目标能量发生大面积扩散, 无法对目标进行有效积累, 处理结果如图 12所示。

下面对本文所提算法的复杂度进行分析。

首先, 需要对接收回波信号进行非均匀子孔径划分, 总脉冲数为Mtotal, 广义二分法非均匀划分的运算复杂度为O(log2Mtotal), 非均匀区间内信号预处理算法的运算复杂度为O(Mtotallog2Mtotal)。

假设距离门个数为N, 动态规划状态转移大小为Nx×Ny, GBM-FrFT-DP非均匀划分子孔径区间大小最大为M, 子孔径个数为K, Chirp Z实现Keystone的点数为Lk, FRFT搜索分数变换阶数为NP, KT-FrFT-质心法均匀分段数为Nk, 段内脉冲数为Mk。具体算法复杂度如表 5所示。本文所提算法的运算复杂度相比均匀分段KT-FrFT质心对齐混合积累算法和传统长时间补偿相参积累算法均有较大程度改善。

设对接收回波信号进行波束形成、脉冲压缩处理后的输入信噪比范围为[-25, 35] dB, 间隔为1 dB, 进行100次蒙特卡洛实验, 得到本文所提算法的位置均方误差结果, 如图 13所示, 得到3种算法的检测性能对比情况，由图 14所示。

位置均方根误差[15]越小, 检测到的目标位置与目标真实位置误差越小, 检测性能越好。经过波束形成、脉冲压缩等处理后，目标输入信噪比达到0 dB以上时, 本文所提算法对目标位置的检测性能达到稳定, 能够对目标位置进行稳定识别。

在本文所提算法生效的信噪比范围内, GBM-FrFT-DP的积累性能要优于均匀分段KT-FrFT质心对齐混合积累算法和传统不分段KT-FrFT相参积累算法。由图 14可见, 当检测概率为0.8时, 所提算法所需的信噪比相比均匀分段KT-FrFT质心对齐混合积累算法低10 dB左右, 相比传统不分段KT-FrFT相参积累算法低20 dB左右。

表1

仿真参数

thumbnail 图7

脉冲压缩结果
表2

区间划分结果

表3

子孔径划分结果

thumbnail 图8

7个子孔径内目标回波信号相参积累结果
thumbnail 图9

GBM-FrFT-DP处理结果
表4

非均匀子孔径划分积累结果

thumbnail 图10

子孔径间目标状态估计结果
thumbnail 图11

KT-FrFT质心对齐处理结果
thumbnail 图12

KT-FrFT长时间相参处理结果
表5

算法复杂度比较

thumbnail 图13

位置均方误差结果图
thumbnail 图14

检测性能对比

4 结论

本文所提GBM-FrFT-DP混合积累算法, 有效解决了长积累时间内难以保证回波信号相干性从而无法对回波信号能量有效积累的问题。首先, 对接收回波信号进行脉冲压缩等预处理, 之后, 结合广义二分法对回波信号进行处理, 完成非均匀区间划分。将目标在同一个距离单元的多个区间信号合并为非均匀子孔径信号。通过对子孔径内的信号进行FrFT, 完成子孔径内目标回波信号跨多普勒单元徙动的校正补偿, 实现子孔径内目标回波信号的相参积累。然后, 对多个子孔径的相参处理结果进行DP操作, 完成子孔径间目标信号的非相参积累。最后, 通过仿真实验验证了所提算法的可行性。

References

  1. GUO Dandan. Target detection method in passive bistatic radar based on beidou Ⅱ satellite signals[D]. Xi'an: Xidian University, 2019 (in Chinese) [Google Scholar]
  2. WANG Di. Research on coherence of passive radar base on space-based signal[D]. Xi'an: Xidian University, 2021 (in Chinese) [Google Scholar]
  3. JI Wenshuai. Radar maneuvering target signal integration algorithm based on segmentation processing[D]. Chengdu: University of Electronic Science and Technology of China, 2021 (in Chinese) [Google Scholar]
  4. GAO L, LI X, WANG M, et al. Joint intra-frame and inter-frame integration method for high speed weak target detection[C]//7th International Conference on Signal and Image Processing, Suzhou, China, 2022: 290–294 [Google Scholar]
  5. ZHAO Y, CHEN Z, ZHANG Y, et al. Hybrid integration method for highly maneuvering radar target detection based on a Markov motion model[J]. Chinese Journal of Aeronautics, 2020, 33: 1717–1730. [Article] [Google Scholar]
  6. CHEN Jie. Reasearch on long-time integration and detection algorithm for maneuvering target based on holographic staring radar[D]. Changsha: National University of Defense Technology, 2019 (in Chinese) [Google Scholar]
  7. LI Z, SANTI F, PASTINA D, et al. Multi-frame fractional Fourier transform technique for moving target detection with space-based passive radar[J]. IET Radar, Sonar & Navigation, 2017, 11(5): 822–828 [Google Scholar]
  8. LI Tang, WANG Feng, YANG Xinyu, et al. Development and status of air target detection from GNSS-based passive radar[J]. Radio Engineering, 2023, 53(7): 1639–1651 (in Chinese) [Google Scholar]
  9. HUANG Lei. Key technology research for GPS based passive radar[D]. Chengdu: University of Electronic Science and Technology of China, 2013 (in Chinese) [Google Scholar]
  10. LIANG Jipeng. Signal enhancement method and measurement data analysis for external radiation source radar of GEO satellite[D]. Xi'an: Xidian University, 2023 (in Chinese) [Google Scholar]
  11. LI Kunhe. Research on technologies related to passive radar[D]. Nanjing: Nanjing University of Science and Technology, 2018 (in Chinese) [Google Scholar]
  12. CHEN Gang. Study on target detection and interference suppression for passive bistatic radar[D]. Xi'an: Xidian University, 2020 [Google Scholar]
  13. CHEN Jiangning. Research on dim target detection technology based on external transmitter of geostationary earth orbit satellite[D]. Chengdu: University of Electronic Science and Technology of China, 2021 (in Chinese) [Google Scholar]
  14. LIU Limin, LI Haoxin, LI Qi, et al. A fast signal parameter estimation algorithm for linear frequency modulation signal under low signal-to-noise ratio based on fractional fourier transform[J]. Journal of Electronics & Information Technology, 2021, 43(10): 2798–2804 (in Chinese) [Google Scholar]
  15. XING Hao. Research on rader weak target track-before-detect algorithm based on dynamic programming[D]. Dalian: Dalian Maritime University, 2020 (in Chinese) [Google Scholar]

All Tables

表1

仿真参数

In the text
表2

区间划分结果

In the text
表3

子孔径划分结果

In the text
表4

非均匀子孔径划分积累结果

In the text
表5

算法复杂度比较

In the text

All Figures

thumbnail 图1

外辐射源雷达系统模型
In the text
thumbnail 图2

二分法处理示意图
In the text
thumbnail 图3

子孔径划分流程图
In the text
thumbnail 图4

区间内信号处理流程图
In the text
thumbnail 图5

区间划分示意图
In the text
thumbnail 图6

算法处理流程图
In the text
thumbnail 图7

脉冲压缩结果
In the text
thumbnail 图8

7个子孔径内目标回波信号相参积累结果
In the text
thumbnail 图9

GBM-FrFT-DP处理结果
In the text
thumbnail 图10

子孔径间目标状态估计结果
In the text
thumbnail 图11

KT-FrFT质心对齐处理结果
In the text
thumbnail 图12

KT-FrFT长时间相参处理结果
In the text
thumbnail 图13

位置均方误差结果图
In the text
thumbnail 图14

检测性能对比
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.