| Issue |
JNWPU
Volume 37, Number 1, February 2019
|
|
|---|---|---|
| Page(s) | 114 - 121 | |
| DOI | https://doi.org/10.1051/jnwpu/20193710114 | |
| Published online | 03 April 2019 | |
Image Fusion Algorithm of Focal Region Detection and TAM-SCM Based on SHT Domain
基于SHT域TAM-SCM与焦聚区域检测的图像融合算法
School of Automation, Northwestern Polytechnical University, Xi’an 710129, China
Received:
6
March
2018
The selection of texture information and block ringing effect in multi-focus fusion process, a new multi-focus image fusion algorithm based on Three Activity Measures (TAM) excitation Spiking Cortical Model, (SCM) in shearlet (SHT) domain is proposed. Firstly, in SHT domain, using local spatial frequency (SF), local energy of gradient (EOG) and different measurements (SF, EOG, and local laplace energy sum (SML)) motivated SCM selected the texture information and construct the initial fusion image (P). Then, the focal region was extracted from the significant feature of the difference between the image P and the original image. Finally, the joint focus area produces fusion images. To verify the superiority of the proposed algorithm, compare the results of this paper with seven competing methods. Experimental results show that the algorithm can produce clear edges, good visual perception and less distortion.
摘要
针对聚焦图像融合过程中细节信息的选取和振铃效应问题,提出了一种基于剪切波(shearlet,SHT)域3种活跃量测(three activity measures,TAM)激发脉冲皮发神经元模型(spiking cortical model,SCM)的多聚焦图像融合新算法。首先,在SHT域,采用局部空间频率(space frequency,SF)和局部梯度能量(energy of gradient,EOG)及不同量测(SF,EOG和局部拉普拉斯能量和(sum-modified-Laplacian,SML))激励SCM模型选择纹理信息并构造初始融合图像P。然后,计算图像P与原图像之间差异的显著性特征提取焦距区域。最后,联合聚焦区域产生融合图像。为了验证提出算法的优越性,将文中结果与7种竞争的方法比较,实验结果表明新算法获得了清晰的边缘,产生了良好的视觉感知和较少的失真。
Key words: image fusion / shearlet transform / spatial frequency / gradient energy / Laplacian energy / focus arear detection / difference image
关键字 : 图像融合 / SHT变换 / 空间频率 / 梯度能量 / 拉普拉斯能量和 / 焦聚区域检测 / 差异图像
© 2019 Journal of Northwestern Polytechnical University
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
当一个场景通过镜头成像时, 在不同深度具有不同数量的模糊目标被捕获, 特别是对仅有有限景深的远距离成像。对于通过照相机捕获的头像, 只有在照相机视野范围内的物体才会被聚焦, 而不在该范围内的目标则非常模糊[1]。多聚焦图像(multi-focus image, MFI)融合的目标是将拍摄的多幅无意义的不同焦点的图像合并成一幅有意义的所有目标都清晰的输出图像。MFI融合被广泛用在遥感、目标识别、显微成像、军事作战及机器视觉等领域。
近年来, MFI融合主要集中于空域方法(spatial domain method, SDM)和转换域方法(transform domain method, TDM)的研究。SDM直接选取像素或区域并使用线性或非线性的方法融合图像[2]。权值平均法、主成分分析法(principal component analysis, PCA)等是一些基于SDM。在空域中, 最简单并且经常使用的融合方法为平均法。这种方法具有空间扭曲、图像模糊等缺点。SDM有优点也有缺点。例如, Brovey方法也是一种SDM, 这种方法具有实现简单、计算时间少等优点, 但也具有输出质量低、空间扭曲严重等缺点[3]。为了解决以上空域方法的不足, 基于转换域的方法被提出。
TDM的思想是将源图像从空间域分解为变换域, 并利用一定的融合规则合并分解系数。最后利用反变换合成已被融合的分解系数得到所需的融合图像。起初, 离散小波变换被应用于MFI图像融合中, 例如, 田静等人利用统计性的拉普拉斯混合模型估计小波系数的分布[4], 提出了基于这类模型的统计清晰量测, 并将其用于MFI融合中。该方法虽能提升融合图像的对比度和清晰度, 但是融合图像丢失信息非常严重。随着多尺度理论的不断发展, 李树涛等人提出了Wavelet与Curvelet变换相结合的MFI融合算法[5]。该算法虽能得到较高的清晰度, 但是所得融合图像的边缘区域确有明显的虚影现象。屈小波等人在非下采样的contourlet变换域采用脉冲耦合神经网络(pulse-coupled neural network, PCNN)链接模型实现了图像融合过程[6]。该方法虽能在一定程度上减少信息量的丢失, 但是该方法运算复杂度非常高, 并且融合图像中显著目标的边缘比较模糊。耿彭等人采用SHT作为分解工具完成了MFI融合[7]。该算法与前面提到的方法相比, 图像的亮度有所提升, 但所得融合图像的边缘区域吉布斯振铃效应非常明显。金鑫等人给出了一种拉普拉斯金字塔变换(Laplacian pyramid transform, LPT)联合局部SF激励PCNN的自适应MFI融合方法[8]。该算法不但能有效实现不同焦聚位置的MFI融合, 而且算法运行的时间比上述所介绍的几种方法都低。可是, 该算法所得图像的对比度比较低, 边缘虚影现象仍未消除。
针对上述问题, 本文提出了一种新的基于SHT域TAM-SCM与差异图像聚焦区域检测的融合算法。首先, 在SHT域中, 为了获得融合图像(P)更多的细节特征, 提出了一种改进SCM喂养输入和点火次数的融合规则选择低频(low frequency, LF)系数。为了更有效的选择中高频(middle high frequency, MHF)和最高频(the highest frequency, THF)中的纹理细节信息, 本文采用EOG[9]和SF[9]的最大值分别选择MHF和THF融合系数。其次, 在空域, 为了测量图像P与源图像间的差异图像的聚焦区域(focus area, FA), 提出了一种基于局部区域拉普拉斯能量和(energy of Laplacian, EOL)的像素检测方法获得FA。然后, 采用形态学技术去掉不合理的成份, 得到新的FA映射。最后, 根据修改后的映射区域合理选择融合图像。采用2组不同背景的MFI进行实验证明, 提出的方法完全利用了新设计的融合规则和EOL检测FA的优势获得了比其他主流的MFI融合更好的效果。
1 相关理论
1.1 SHT变换
在实际应用方面, SHT是一种多尺度框架, 它允许在典型的多变量问题中对二维图像的各向异性特征进行有效的编码。与小波变换类似, SHT变换起源于仿射群, 允许统一处理连续体和数字情况, 才能将其可靠实现。在参考文献[10]中, SHT表示为:
式中,  , a>0, 表示改变分辨率的二维各向异性的尺度矩阵,
, a>0, 表示改变分辨率的二维各向异性的尺度矩阵, 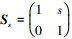 , s∈R为用于改变方向的二维可逆剪切矩阵。最后, SHT可以通过Ψa, s, t(x)函数来构造。
, s∈R为用于改变方向的二维可逆剪切矩阵。最后, SHT可以通过Ψa, s, t(x)函数来构造。
Ψ∈L2(R2)满足以下条件:对于任何ξ=(ξ1, ξ2)∈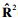 (ξ2≠0), 我们假设
(ξ2≠0), 我们假设 (ε1, ε2)=
(ε1, ε2)=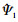 (ε1)
(ε1)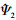 (ε2/ε1), 其中
(ε2/ε1), 其中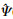 (ε)表示Ψ(ε)的傅里叶变换, Ψ1是连续小波。
(ε)表示Ψ(ε)的傅里叶变换, Ψ1是连续小波。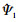 ∈C∞(R), suppΨ1⊂[-2, -1/2]∪[1/2, 2]。
∈C∞(R), suppΨ1⊂[-2, -1/2]∪[1/2, 2]。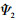 ∈C∞(R), suppΨ2⊂[-2, -1/2]∪[1/2, 2], 其中,
∈C∞(R), suppΨ2⊂[-2, -1/2]∪[1/2, 2], 其中, 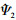 ≥0并且‖Ψ2‖=1。
≥0并且‖Ψ2‖=1。
我们假设:
对于任意:j≥0
利用 和
和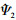 所支撑得条件, 函数Ψj, l, k所具有的频率支撑给出如下:
所支撑得条件, 函数Ψj, l, k所具有的频率支撑给出如下:
也就是说, 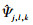 的每一个元素由一对梯形支撑, 它的尺寸大小近似为22j×2j并沿着l2-j的斜线方向, 如图 1a)所示。
的每一个元素由一对梯形支撑, 它的尺寸大小近似为22j×2j并沿着l2-j的斜线方向, 如图 1a)所示。
从方程式(2)和(3)可以看出, 对于任意(ξ1, ξ2)∈D0={(ξ1, ξ2)∈R2: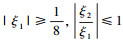 }, 有如下方程:
}, 有如下方程:
函数集合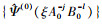 构成的D0部分如图 1b)所示。
构成的D0部分如图 1b)所示。
D0被支撑在区间[-1/2, 1/2]2内, 因此
形成函数L2(D0)∨={f∈L2(R2):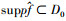 }的帕斯威尔框架。
}的帕斯威尔框架。
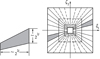 |
图1 SHT的频域支撑和频域平面剖分图 |
1.2 SCM的数学模型
作为基于人工神经网络(artificial neuron network, ANN)的新成员, SCM联合了PCNN和交叉皮层模型(intersecting cortical model, ICM)的优势[11]。SCM的神经元能够表示为Nij, 它由接收单元、调制机构和脉冲产生3个部分组成。SCM神经元的构成见图 2。
SCM模型的离散数学形式被描述如下:
如图 2所示, 在接收域, Nij通过其他神经和外部源2个通道接收收入信号。一个通道是喂养收入Sij, 另一个通道是连接收入Lij, 它分别对应于方程(7)和(8), Uij为内部活动行为, 它以二阶模型的形式联合以上两通道的信息形成总的内部活动行为, 如方程(9)所示。根据方程(10), Eij为动态阈值, 它与输出Yij相比影响神经的点火频率。方程(11)表示Uij与Eij相比决定输出值Yij。如果在方程(11)中需求得到满足, 神经元Nij将被激活并产脉冲, 它的特点是Yij=1, 否则Yij=0。结果是以自动波的形式从活跃区域扩展到整个区域。
除了以上讨论的参数, 这里仍然有6个其他参数包括:VL, Wijkl, f, g, h和γ需要解释。VL是幅度比例项; Wijkl是连接矩阵; f和g表示恒定常数; h阈值幅度系数; γ表示sigmoid函数的参数。显然, 在参数的总数量和操作机制方面, SCM的结构比传统的PCNN更加紧凑。
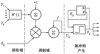 |
图2 SCM神经元的结构 |
2 提出的多聚焦图像融合算法
本小节所提出的基于SHT域TAM-SCM的MFI的算法描述如图 3所示。该方法主要通过SHT域和空域来实现, 其具体实现细节给出如下。
 |
图3 提出的MFI融合算法框图 |
2.1 SHT域的多聚焦图像融合
在本小节, 一种基于SHT域采用新设计的不同融合方案分别合成高低频系数的实现过程描述如下:
1) 给定测试源图像A和B。
2) 通过SHT剖分图像A和B得到其对应的低频子带系数集{LFSHTA, LFSHTB}, MHF和THF子带系数集{MHFSHTA, MHFSHTB}, {THFSHTA, THFSHTB}, 并且将SHT的分解级数定为3层。
3) LF系数应用最新设计的融合方案来得到新合成系数LFSHTF, 其实现的详细过程将在下一部分给出。
4) 对MHF和THF图像分别采用局部EOG和SF获得新高频系数MHFSHTF和THFSHTF。
5) 采用逆剪切波(inverse shearlet, ISHT)从融合的子带系数中重构出融合图像P。
2.1.1 低频系数融合
step 1 对于LF系数的融合, 3种不同活跃量测激励SCM的融合方案被提出, 这3种不同融合方案分别被命名为:融合方案-1(fusion scheme-1, FS-1), 融合方案-2(fusion scheme-2, FS-2), 和融合方案-3(fusion scheme-3, FS-3)。其中, FS-1, FS-2和FS-3所用到的外部激励分别为局部SF, 局部EOG, 和局部SML[9]。
对于FS-1:计算LF系数的局部SF:
式中, M和N表示局部区域窗口的大小, LFSHTX表示图像A和B的LF子带系数, X表示图像A和B。
对于FS-2:利用方程式(13)计算LF的局部EOG:
对于FS-3:按照公式(14)计算LF系数的局部SML值:
step 2 采用以上步骤计算的局部SF, 局部EOG和局部SML单独作为外部输入激励SCM并将数学关系建立的神经脉冲给出如下:
step 3 经n次迭代后计算点火时间。
式中, R分别表示外部激励SF, EOG和SML。
step 4 计算3种不同外部激励的点火次数
式中, Tij, TX[n], Tij, SFX[n], Tij, EOGX[n]和Tij, SMLX[n]分别表示总的点火次数(fire time, FT), 基于FS-1局部SF激励SCM的FT, 基于FS-2局部EOG激励SCM的FT, 基于FS-3局部SML激励SCM的FT。
step5 基于总FT和LF系数绝对值设计的混合融合规则为:
式中, LFSHTF为设定的阈值, LFSHTF为LF融合系数。
2.1.2 高频系数融合
在SHT剖分所得的高频系数中, MHF系数能够反映粗糙的细节信息, 而图像的局部EOG能够很好地反映MHF中的显著特征, 因此, 采用基于局部EOG最大值方案来选择MHF系数的最大活跃级。MHF系数的局部EOG被计算如下:
对于MHF系数的融合, 具有最大MEOG特征的系数被选择为融合系数, MHF系数的融合方案给出如下:
式中, MEOGijA和MEOGijB分别为图像A和B所对应的MHF系数的局部EOG值。MHFSHTF表示融合后的MHF系数。
THF系数中包含了精确的纹理细节信息, 图像的局部SF能够有效地描述精确信息的活跃程度, 因此, 对于THF系数的融合, 基于THF系数局部SF特征取大的融合方案被选用。THF系数的局部SF被定义如下
对于THF子带系数的融合, 具有最大TSF特征值的子带系数被选择为融合系数, THF的融合方案可通过如下方程式(23)获得:
式中, THFSHTF表示融合后的THF系数, TSFijA与TSFijB分别为图像A和B的THF系数所对应的局部SF值。
2.2 空域的焦聚区域检测
图像经过SHT域的融合之后, 能够看出一些重要的信息并不能通过SHT域所制定的融合方案提取出来。主要是因为SHT域内尺度的收缩, 以及在SHT域所提取的特征并不能成功用到每个系数上。为了解决此问题, 在空域, 提出了基于局部EOL检测焦聚区域的算法, 该算实现的细节描述如下。
2.2.1 图像差异
图像差异(image difference, ID)能够用于评价融合性能的有效性, 对于去焦图像, 可以看出不同的ID能够反映图像的不同。基于初始融合结果的不同ID可以给出如下:
式中,A(i, j), B(i, j)和P(i, j)分别表示源图像和图像P在(i, j)处的像素值。
2.2.2 焦聚区域检测
为了获得差异图像去模糊区域的显著性特征, 本文采用ID局部区域的EOL[9]作为量测, 检测ID的聚焦区域, ID的局部EOL特征可以给出如下:
利用方程(25)所得ID的局部EOL特征检测聚焦区域, 其检测结果如下所示
式中, EOLA和EOLB分别为差异图像A和B的EOL值, 1为输入图像A在位置(i, j)处的聚焦区域, 0为输入图像B在(i, j)处的聚焦区域。
在矩阵H(i, j)中,包含有黑洞,沟壑等现象,为了消除这些现象,本文采用文献[19]所提供的形态,滤波技术对矩阵H(i, j)进行滤波处理,得到新的决策矩阵HH(i, j)。根据HH(i, j)矩阵可确定出最终的融合图像F为:
3 实验结果与相关分析
3.1 实验建立
为了验证提出算法具有更好的性能, 本文选取“Clock(256×256)”、“Desk(320×240)”2组聚焦图像集与主流的图像融合算法进行对比。这些对比算法分别为基于比率金子塔的方法(RP)[12]、基于FDCT的方法[13]、Wang′s的方法[14]、基于NSCT-PCNN的方法[6]、基于RPCA的方法[15]、基于LW的方法[8]及NWGE的方法[16]。其中, 以上7种方法所需的参数设置与其对应的文章相同, 而本文方法SHT的分解层数设置为3层, 阈值δ设置为50, SCM模型所需参数为:n设为40;g, f, h, γ分别为0.7, 0.8, 20和1;连接域的权值矩阵W=[0.109 1, 0.140 9, 0.109 1;0.140 9, 0, 0.140 9;0.109 1, 0.140 9, 0.109 1]。
3.2 客观评价指标
为了更好地评价融合图像的感知质量, 我们采用视觉对比和定量估计联合的方法进行评估。因此, 能够评估融合结果感知质量的标准与人类视觉主观一致是非常必要。在本文中, 我们使用3种流行的质量指数确定提出方法的有效性和优越性, 命名为:基于信息量的标准MI[17], 相似性度量的标准SSIM[18], 边缘质量的标准QAB/F[17]。以上提到的3种标准所对应的指数值越大, 表明图像的质量越好。
3.3 实验结果分析
3.3.1 主观性能分析
图 4给出了多聚焦“Clock”图像集的融合结果。图 4a)~图 4b)分别对应左聚焦和右聚焦图像。图 4c)~4j)为7种竞争方法和提出方法所得融合结果。通过部分放大区域的视觉观察, 可以得出图 4g)融合图像的整体比较清晰, 但边缘振铃效应比较明显。
图 4c)~4f)、图 4h)分别与图 4g)相比, 融合图像中或多或少都存在边缘扭曲和振铃效应。其中, 图 4c)的边缘失真表现最为明显。主要原因是在变换域中设计不同的融合规则不能很好选取纹理信息所致。图 4i)与前面的几种竞争方法相比, 能得到较好的融合效果, 但仍存在信息冗余现象。相反, 提出的融合方法包含源图像所有有用的信息。而且, 从图 4j)可以看出提出方法产生最接近理想融合图像的结果。
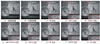 |
图4 “Clock”数据集的实验结果 |
3.3.2 客观性能分析
从表 1提供的3种测试数据和不同融合算法的MI, SSIM, 和QAB/F的值可以看出, 本文算法的3种质量指数值明显优于其他对比方法。图 4g)的3种指标值最低。图 4i)的MI, QAB/F值高于其他的对比方法, 低于本文的方法, 而它的SSIM值略低于LW的方法。然而, MI, QAB/F的值高于其他7种算法, 这表明提出的方法有更好的边缘保持能力, 并且在融合信息转换过程中丢失信息量最少。
一种数据8种方法的定量评价结果
4 结论
一种新颖的基于SHT域与空域的MFI融合算法被提出。首先, 在SHT域, 提出TAM-SCM模型融合技术获得初始融合图P。然后, 在空域, 计算P与输入图像差异的EOL特征检测输入图像的聚焦区域。最后, 采用形态学的后处理技术修改决策映射, 并选择聚焦区域的像素得到融合图像。客观性能评估标准和视觉观察证明提出的方法优于各种存在的基于空域和变换域的方法。
References
- Xiao J, Liu T, Zhang Y, et al. Multi-Focus Image Fusion Based on Depth Extraction with Inhomogeneous Diffusion Equation[J]. Signal Processing, 2016, 125(5): 171-186 [Article] [CrossRef] [Google Scholar]
- Aymaz S, KÖse C. A novel Image Decomposition-Based Hybrid Technique with Super-Resolution Method for Multi-Focus Image Fusion[J]. Information Fusion, 2019, 45(12): 113-127 [Article] [CrossRef] [Google Scholar]
- Brahmbhatt K N, Makwana R M. Comparative Study on Image Fusion Methods in Spatial Domain[J]. Int J Adv Res Eng Technol, 2013, 4(2): 161-166 [Google Scholar]
- Tian J, Chen L. Adaptive Multi-Focus Image Fusion Using a Wavelet-Based Statistical Sharpness Measure[J]. Signal Processing, 2012, 92(9): 2137-2146 [Article] [CrossRef] [Google Scholar]
- Li S T, Yang B. Multifocus Image Fusion by Combining Curvelet and Wavelet Transform[J]. Pattern Recognition Letters, 2008, 29(9): 1295-1301 [Article] [CrossRef] [Google Scholar]
- Qu Xiaobo, Yan Jingwen, Xiao Hongzhi, et al. Image Fusion Algorithm Based on Spatial Frequency-Motivated Pulse Coupled Neural Networks In Nonsubsampled Contourlet Transform Domain[J]. Acta Automatica Sinica, 2008, 34(12): 1508-1514 [Article] [CrossRef] [Google Scholar]
- Geng P, Wang Z, Zhang Z, et al. Image Fusion by Pulse Couple Neural Network with Shearlet[J]. Optical Engineering, 2012, 51(6): 067005 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Jin X, Hou J, Nie R, et al. A Lightweight Scheme for Multi-Focus Image Fusion[J]. Multimedia Tools and Applications, 2018, 30(5): 1-27 [Article] [Google Scholar]
- Huang W, Jing Z. Evaluation of Focus Measures in Multi-Focus Image Fusion[J]. Pattern Recognition Letters, 2007, 28(4): 493-500 [Article] [CrossRef] [Google Scholar]
- Easley G R, Labate D, Lim W Q. Optimally Sparse Image Representations Using Shearlets[C]//Fortieth Asilomar Conference on Signals, Systems and Computers, 2006: 974-978 [Google Scholar]
- Kong W, Lei Y, Zhao R. Fusion Technique for Multi-Focus Images Based on NSCT-ISCM[J]. International Journal for Light and Electron Optics, 2015, 126(21): 3185-3192 [Article] [CrossRef] [Google Scholar]
- Liu Y, Liu S, Wang Z. A General Framework for Image Fusion Based on Multi-Scale Transform and Sparse Representation[J]. Information Fusion, 2015, 24(3): 147-164 [Article] [CrossRef] [Google Scholar]
- Hang L H G. Research on Image Fusion Based on the Second Generation Curvelet Transform[J]. Acta Optica Sinica, 2006, 26(5): 657-622 [Article] [Google Scholar]
- Wang N, Ma Y, Wang W, et al. Multifocus Image Fusion Based on Nonsubsampled Contourlet Transform and Spiking Cortical Model[J]. Neural Network World, 2015, 25(6): 623 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Li H, Li L, Zhang J. Multi-Focus Image Fusion Based on Sparse Feature Matrix Decomposition and Morphological Filtering[J]. Optics Communications, 2015, 342(56): 1-11 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Zhou Z, Li S, Wang B. Multi-Scale Weighted Gradient-Based Fusion for Multi-Focus Images[J]. Information Fusion, 2014, 20(5): 60-72 [Article] [CrossRef] [Google Scholar]
- Hossny M, Nahavandi S, Creighton D. Comments on Information Measure for Performance of Image Fusion[J]. Electronics letters, 2008, 44(18): 1066-1067 [Article] [CrossRef] [Google Scholar]
- Xydeas C S, Petrovic V. Objective Image Fusion Performance Measure[J]. Electronics Letters, 2000, 36(4): 308-309 [Article] [CrossRef] [Google Scholar]
- Du C, Gao S. Multi-Focus Image Fusion Algorithm Based on Pulse Coupled Neural Networks and Modified Decision Map[J]. International Journal for Lignt and Electorn Optics, 2018, 157(5): 1003-1015 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图1 SHT的频域支撑和频域平面剖分图 |
| In the text | |
 |
图2 SCM神经元的结构 |
| In the text | |
 |
图3 提出的MFI融合算法框图 |
| In the text | |
 |
图4 “Clock”数据集的实验结果 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


