| Issue |
JNWPU
Volume 37, Number 6, December 2019
|
|
|---|---|---|
| Page(s) | 1257 - 1263 | |
| DOI | https://doi.org/10.1051/jnwpu/20193761257 | |
| Published online | 11 February 2020 | |
Universal Filtered Multi-Carrier System Based on Selective Mapping
基于选择映射的通用滤波多载波系统
1
School of Electronics and Information, Northwestern Polytechnical University, Xi'an 710072, China
2
School of Physics and Telecommunication Engineering, Zhoukou Normal University, Zhoukou 466000, China
Received:
15
November
2018
Internet of things (IoT) and machine-to-machine (M2M) communication are characterized by short periods and bursts. Traditional orthogonal frequency division multiplexing (OFDM) has not meet the demand for such traffic, while IoT and M2M communication will play an important role in the next fifth generation (5G) communication, so it is particularly urgent to study the small packet and low-latency wireless transmission technologies that satisfy IoT and M2M communication. Universal filter multi-carrier (UFMC) is a new kind of filtered wireless transmission mechanism that meets this requirement, but it faces a higher peak-to-average power ratio (PAPR) than OFDM, which affects the energy efficiency of UFMC. Based on the PAPR performance evaluation of several multi-carrier transmission technologies, a universal filtered multi-carrier based on selective mapping (SLM-UFMC) system is proposed, and the relationship between the number of candidate sub-bands and the performance or between the number of carriers and the performance is carried out. The simulation results show that SLM-UFMC can effectively reduce the PAPR of UFMC system, and the PAPR performance is improved by 1.8 dB comparing with the traditional UFMC. It also further indicates that SLM-UFMC is more suitable for IoT and M2M communication in 5G communication.
摘要
物联网(internet of things, IoT)和机器对机器(machine-to-machine, M2M)通信的特点是周期短且突发,传统的正交频分复用技术(orthogonal frequency division multiplexing, OFDM)已经不能适应这种流量的需求,而IoT和M2M通信在未来第五代(fifth generation, 5G)通信中又将占据重要的地位,因此研究满足IoT和M2M通信的小包低时延无线传输技术显得尤为迫切。通用滤波多载波技术(universal filtered multi-carrier, UFMC)正是满足这种需求的一种新型滤波无线传输机制,但是它面临着比OFDM更高峰均功率比(peak-to-average power ratio, PAPR)的问题,这影响了UFMC的能效效率。在对几种多载波传输技术PAPR性能评估的基础上,提出了一种基于选择映射的通用滤波多载波系统(universal filtered multi-carrier based on selective mapping, SLM-UFMC),并对候选子带个数和载波数与性能之间的关系进行了探究。仿真结果表明:SLM-UFMC能够有效地降低UFMC系统的PAPR,相对于传统UFMC,PAPR性能提高多达1.8 dB。这也进一步表明SLM-UFMC更加适合于5G通信中的IoT和M2M通信。
Key words: SLM / UFMC / OFDM / PAPR / SLM-UFMC
关键字 : SLM / UFMC / OFDM / PAPR / SLM-UFMC
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
过去几年, 长期演进技术升级版(long-term-evolution-advanced, LTE-Advanced)的商用化基本满足了人们对于语音、视频、网络等多元传输的需求。但是随着海量物联设备和全新应用场景不断出现, 例如:无人驾驶、人工智能、增强现实以及移动社交等。现有的第四代网络已经不能满足未来通信的需求, 在此背景下5G[1]应运而生。5G将主要解决多场景下面临的性能挑战问题, IoT和M2M通信将成为5G通信的主要驱动力。
第五代移动通信技术推进组发布的5G无线技术架构白皮书从使用场景和关键技术方面归纳了5G的3个主要应用场景[2], 分别是增强型的移动宽带场景(enhanced mobile broadband, eMBB), 超高可靠和低延迟的通信场景(ultra-reliable and low latency communications, uRLLC)和大规模的机器类通信场景(massive machine type communications, mMTC), 他们都必须是未来5G通信系统的一部分。这就要求5G综合考虑峰值速率、频谱效率、网络能效以及延迟等多项指标, 有效地支持多种类型业务, 并满足大容量、多接入、高移动性、高速率和低时延的特性。在此需求下, 亟待设计新的无线空口技术满足多场景和灵活部署的需求。特别是研究面向IoT和M2M通信的小包低时延无线传输技术显得尤为迫切。
OFDM[3]以其较低的复杂度以及可充分利用分集增益的优势广泛应用于通用移动通信技术的长期演进、全球微波互联接入、无线热点、无线局域网、数字视频广播、非对称数字用户线路等多种场合。但是较高的峰值功率和固定的符号时长、严格的时间同步限制了它在技术进化过程中的进一步发展, 而具有较低的峰均功率比的绿色节能的智能终端必将是未来无线网络的主要接入设备, 这就使得人们需要寻求更加多元的传输技术。在文献[4]中, 基于离散傅里叶变换扩展和同时移位多载波条件, 作者提出了一种基于滤波器组的低峰均功率比多载波(low PAPR filter bank multi-carrier, LFBMC)技术, 具有分数复杂度开销和较低的PAPR, 计算复杂性开销和边带信息开销都有所降低。但LFBMC是传统滤波器组多载波(filter bank multi-carrier, FBMC)技术的改进, 继承了FBMC固有的缺点。比如, 不能有效获得多天线技术所带来的系统增益。最近一段时间正在讨论的低复杂度广义频分复用技术(low complexity generalized frequency division multiplexing, LGFDM)[5]由于其吸引人的特性而被学者们广泛关注。块傅里叶变换矩阵使调制矩阵稀疏化,结合矩阵的特殊块循环特性大大降低了结构的复杂性, 而且不会导致性能的损失。但是, 当调制矩阵为奇异矩阵时, LGFDM技术受到限制。
UFMC[6]正是满足小包低时延无线传输特性的一种新型滤波传输机制。通过把整个频带划分为若干组子带, 对每组子带进行滤波处理, UFMC降低了滤波器的长度和带外功率。采用QAM的调制方式, 这保证它可以结合多天线技术获得足够的分集增益来提高性能, 非常适合短上行链路突发通信或低延迟通信。但是, 较高的PAPR影响了UFMC的能效效率, 也不符合5G绿色通信的要求。
多载波系统中PAPR问题的传统解决方案是降低非线性功率放大器的工作点, 这种方法通常导致显著的功率效率损失。为解决这个问题, 研究人员提出了各种方案[7]。比如:限幅法(amplitude clipping and filtering, ACF)、星座图扩展法(active constellation extension, ACE)、选择性映射法(selected mapping, SLM)和部分传输序列法(partial transmit sequence, PTS)。其中, SLM因较好的性能和没有干扰吸引了大量学者的关注。虽然OFDM的PAPR已被我们熟知, 但是UFMC的PAPR研究却没有得到足够重视。根据目前查阅文献的情况, RONG等在文献[8]中提出了一种低复杂度的PTS用来降低UFMC的PAPR, 但系统性能有所下降。文献[9]调查了5G中降低PAPR的一些技术, 包括SLM和子载波预留技术, 但有待深入研究。
在本文中, 一种结合SLM和UFMC的通用滤波多载波系统SLM-UFMC被提出来。通过子带映射的方法将SLM和UFMC结合, UFMC的高PAPR问题得到有效改善。仿真结果也表明, SLM-UFMC能够降低UFMC的PAPR多达1.8 dB在CPAPR=10-4, 并且随着候选子带的增加, SLM-UFMC的性能也进一步提高。这也使得SLM-UFMC更加符合5G绿色通信的需求, 而且本文方法很容易和非正交多址技术结合进一步提高系统的容量。
1 通用滤波多载波系统
通用滤波多载波系统的典型结构[10]如图 1所示, 为方便分析, 这里只考虑单用户情况, 多用户场景可依次类推。在图 1中, 总数为N的子载波被划分为B个子带, 即每个子带具有n=N/B个子载波, 第i个子带具有的子载波数为ni(i=1, 2, …, B)。实际操作中, 可以让每个子带具有不相等数目的子载波, 也可以让其具有相同数目的子载波, 为了简单起见, 一般情况下默认每个子带采用等数目分割的方法, 此时ni=n。如果不采用等数目分割的方法, ni≠n, 有∑ni=N(i=1, 2, …, B)。在发射端, 特定数量的比特信息通过格雷码M进制正交幅度调制(M-ary quadrature amplitude modulation, M-QAM)映射到符号S上。然后这些符号通过载波划分的方式被分配到每一个子带上, 其中第i个子带分到的频域符号是Si(i=1, 2, …, B), 长度是ni。然后这些符号Si通过N点快速逆傅里叶变换(IFFT)转换到时域信号si。对于第i个子带, 时域信号si可以被表示为
式中, Oi是第i个子带中的子载波索引集[11]。然后, UFMC在每一个子带上执行滤波处理, 不同于FBMC对每一个子载波进行滤波处理, 滤波后的信号xi可以看做是有限长单位冲激响应(finite impulse response, FIR)滤波器脉冲响应fi与时域信号si的线性卷积的结果。通过子带滤波的方式, UFMC放松了对于定时同步的要求, 增强了频率和时间失准的鲁棒性。由于没有引入循环前缀的操作, 提高了系统的频谱效率。因此, 对所有的子带进行叠加求和, 时域叠加后的信号x, 也就是发射端送出的信号, 可以表示为
式中, *表示线性卷积操作, L是FIR滤波器长度。
对时域叠加的信号x进行上变频和RF处理, 接收端检测器接收到噪声叠加的信号, 通过把带通信号转换到基带信号, 在时域中对接收到的信号进行处理。一般情况下认为正交频分复用多载波系统是UFMC的一种特殊情况(滤波器L=1)。
对于接收到的信号y, 常规做法是对其进行零填充操作, 也就是在接收信号的后面补上一定数目的零, 使接收信号的长度达到发送信号的2倍即2N。然后对这2N点接收信号进行快速傅里叶变换, 将时域的信号转化到频域信号Y, 可以通过线性均衡的方法(比如:迫零均衡或最小均方误差均衡。)从接收信号中恢复出发送信号Yi(i=1, 2, …, B)。
 |
图1 通用滤波多载波系统典型结构图 |
2 基于选择映射的通用滤波多载波系统
在SLM-UFMC中, 总数为N的子载波首先被划分为B个子带, 然后将每一个子带扩展为U个不同的候选子带, 这样, 发送端共产生了BU个不相同的候选子带, 这些候选子带都包含了原始传送的数据信息, 经过IFFT和滤波处理后从这BU个候选子带选出B个具有最小PAPR的子带进行叠加传输。图 2给出了基于选择映射的通用滤波多载波系统的系统框图, 对于BU个候选子带, 每个候选子带都乘以一组旋转因子B(u)=[bu, 0, bu, 1, …, bu, N/B-1]T, 这里u=1, 2, …, U。不同的旋转因子可能带来不相同的系统性能, 比如循环移位序列, 哈达玛序列或黎曼序列等。旋转后的信号可以表示为
式中, i=1, 2, …, B, j=1, 2, …, U。
频域中的信号通过快速傅里叶逆变换转换到时域中, 这个过程可以表示为
式中, Si, j(k)是频域中的候选信号, Oi是第i个子带中的子载波索引集。通过对每一组子载波进行滤波处理fi(i=1, 2, …, B), 可以得到滤波后的信号xi, j(l)。为简化分析, 这里对U个候选子带采用相同的滤波处理。可以表示为
式中, *表示线性卷积操作, si, j(l)表示时域信号, i=1, 2, …, B, j=1, 2, …, U。发送端从这BU个候选子带中选出PAPR最小的B个子带xi进行发送, 这里i=1, 2, …, B。选择的子带索引以及旋转因子信息以边带信息的形式传送到接收端来重现接收到的信号信息。
式中,i, j同上, min{·}表示PAPR最小。选出的信号在时域进行叠加后形成新的发送信号可表示为
如果用矩阵的方式重写上式, 公式(7)可以改写为
式中, F=[F1, F2, …, FB], V=Λ[V1, V2, …, VB], 这里Λ表示diag矩阵, S=[S1, jT, S2, jT, …, SB, jT]T, j=1, 2, …, U, 表示经过最小PAPR选择后所要发送的频域信号, SB, j是和min{xB, 1, xB, 2, …, xB, U}相对应的发送信号。Vi(i=1, 2, …, B)是一个N×ni维的矩阵, 根据在整个可用频率范围内的相应子带位置它从逆傅里叶变换矩阵中抽取ni列向量构成, 所有子带的变换矩阵刚好组成一个完整的逆傅里叶变换矩阵。V是一个对角矩阵, 主对角线上的子矩阵分别是V1, V2, …, VB。Fi是一个(N+L-1)×N维的Toeplitz矩阵(L是线型滤波器的长度, 不同子带的滤波长度可以不同, 载波间隔也可以不相同), 其每一列都是由相应子带位置上的滤波器脉冲响应系数进行循环移位后得到的, Fi是可以根据系统的传播条件和时频偏移调节的, Si是一个ni×1维的矩阵, i=1, 2, …, B。
假设系统具有完美的同步措施, 经过信道后的接收信号y可看做信号x与信道h的卷积形式, 这个过程可以表示为
式中, h是长度为r的信道的时域冲击响应, *表示与信号x进行线性卷积, H是一个与信道冲击响应相关的Toeplitz矩阵, 它的第一列元素是[hT, 01×(N+L-2)]T, 它的第一行元素是[h(0), 01×(N+L-2)]T, n是一个(N+L+r-2)维的复高斯白噪声。公式(9)可以进一步改写为
式中, H是一个与信道冲击响应相关的Toeplitz矩阵, F是由Toeplitz矩阵构成的矩阵, V是一个由逆傅里叶变换矩阵构成的对角矩阵, S是经过选择后所要发送的频域信号构成的信号矩阵, n是一个(N+L+r-2)维的复高斯白噪声。
对于接收到的信号y, 传统的做法是对其进行补零操作, 也就是在接收信号的后面补上一定数目的零, 使其接收信号的长度为2N。然后对这2N点接收信号进行快速傅里叶变换, 将时域的信号转化到频域信号Y。这个过程可以表示为
式中, W是2N点FFT变换矩阵, P是一个扩展的单位阵, 它可以写成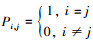 , 把P写成矩阵形式,
, 把P写成矩阵形式, 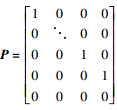 (P是一个2N×(N+L+r-2)的矩阵)。接收信号Y中处于偶数位的信号是需要解调的信号, 奇数位信号是干扰信号, 一般情况下需要舍去处于奇数位的信号, 而只解调偶数位的信号。这个操作过程可以用一个2N×N矩阵Pi去实现,
(P是一个2N×(N+L+r-2)的矩阵)。接收信号Y中处于偶数位的信号是需要解调的信号, 奇数位信号是干扰信号, 一般情况下需要舍去处于奇数位的信号, 而只解调偶数位的信号。这个操作过程可以用一个2N×N矩阵Pi去实现, 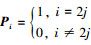 , 也就是
, 也就是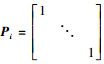 (Pi是一个2N×N的矩阵)。除去干扰信号后的解调信号Yi可以表示为
(Pi是一个2N×N的矩阵)。除去干扰信号后的解调信号Yi可以表示为
如果令Φ=PiTWPHFV, 文献[6]表明Φ是一个对角阵。因此, 信号Yi, i=1, …, B, 仅仅依赖于发送信号Si, j和对角矩阵Φ。线性均衡的方法可以用来从接收信号中直接恢复出发送信号, 不失一般性, 迫零均衡和最小均方误差均衡可以用来复原信号。
式中, S(k)表示均衡后的信号。假设接收端具有旋转因子的发送副本, 那么均衡后的信号进行旋转因子的反操作, 便可以重构原始的发送信号。
SLM-UFMC系统的峰均功率比可以定义为
式中, E[|x(l)|2]表示信号的平均功率, max[|x(l)|2]表示信号的最大功率, x(l)如公式(7)所示。因为单个信号的PAPR并不能反映信号的统计特性, 因此, 通常用互补积累分布函数(complementary cumulative distribution function, CCDF)描述系统的PAPR特性, 即LPAPR大于给定阀值LPAPR0的概率
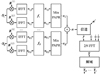 |
图2 基于选择映射的通用滤波多载波系统框图 |
3 仿真分析
在这一部分, 通过仿真来验证SLM-UFMC系统PAPR性能的优越性, 图 3和图 4展示了OFDM、UFMC、SLM-OFDM和SLM-UFMC系统在不同载波数下PAPR性能的对比情况。为了全面评估系统性能, 采用两组实验对照, CCDF被用来评估系统的PAPR性能。图 3采用512个子载波, 图 4采用128个子载波。同时采用16QAM调制方式, 道尔夫-切比雪夫滤波器的长度为43, 旁瓣衰减是40 dB。旋转因子采用从{+1, -1, +j, -j}随机选取的方法, 候选子带数是U=8。
从图 3中可以看到, 传统的UFMC相比于OFDM面临着更加严重的PAPR问题, 这可能是因为子带滤波器脉冲响应不等于1增加了符号长度进而影响了系统PAPR的统计特性。这也为UFMC在IoT和M2M通信中的应用提出了一个迫切需要解决的问题, 那就是如何解决UFMC高PAPR问题。同时也能够清楚地从图 3中看到UFMC的PAPR性能下降了0.3 dB,相对于传统OFDM来说, 在CPAPR=10-3。采用SLM的方法, 可以降低OFDM的PAPR, SLM-OFDM相比于OFDM来说, 在CPAPR=10-4, 性能提高了大约3 dB。而且, 相对于UFMC来说, SLM-UFMC性能也提高了0.5 dB在CPAPR=10-4。同时, 也应该注意到, 在同样的条件下, SLM-OFDM的性能要好于SLM-UFMC的性能。在CPAPR=10-4, 两者的性能相差2.8 dB。这和前面讨论的观点相一致, 也就是说在同样的条件下, UFMC比OFDM面临着更严重的PAPR问题。
图 4给出了128个子载波时, OFDM、UFMC、SLM-OFDM和SLM-UFMC系统PAPR性能对比。从图中可以看到, 当载波数变少的时候, SLM-UFMC仍然能够较好地提高UFMC的PAPR性能。比如, CPAPR=10-4, SLM-UFMC比UFMC的PAPR性能提高了1.8 dB。同时, UFMC相比于OFDM, 面临着更严重的PAPR问题。在CPAPR=10-4, 两者相差了大约0.2 dB。从图 3和图 4对比来看, 无论是OFDM还是UFMC, 128个子载波都比512个子载波具有更好的性能。举例来说, 在CPAPR=10-4, UFMC相差了大约0.2 dB。这可能是因为其载波数目较少, 使得步调一致的子载波数目较少进而导致系统叠加峰值功率较小的原因。从图 3和图 4的对比也可以得出结论:OFDM、UFMC、SLM-OFDM和SLM-UFMC的PAPR性能都和载波数有关, 载波数越多, 系统PAPR性能越差。
SLM-UFMC的PAPR性能与候选子带个数U之间的关系如图 5所示, 候选子带个数U的取值分别为4, 8, 16, 64。从图中可以得到, 随着候选子带个数的增加, 可以选择的候选信号副本数变多, 可选择发送信号的范围增大, 系统的性能随着U值的增大越来越好。在CPAPR=10-4, SLM-UFMC的PAPR在U=64相比于U=4来说可以提高将近1 dB。当然, 这里性能提升是以牺牲了部分复杂度为代价, 候选子带个数U越大, 需要的IFFT个数增多, 系统复杂度提高。但是随着硬件技术的发展, 复杂度可能不会是限制一项新技术应用的瓶颈。
因此, 在某些硬件不受限的情况下, 本文提出的SLM-UFMC也不失为一种解决UFMC高PAPR问题的有效方法。这就使得SLM-UFMC更加符合5G绿色通信的需求, 而且它很容易和非正交多址技术结合进一步提高系统的容量。同时, 这也为UFMC在未来5G以及IoT和M2M通信中的大规模应用奠定了基础。
 |
图3 N=512时, OFDM、UFMC、SLM-OFDM和SLM-UFMC系统PAPR性能对比 |
 |
图4 N=128时, OFDM、UFMC、SLM-OFDM和SLM-UFMC系统PAPR性能对比 |
 |
图5 不同候选子带个数下SLM-UFMC PAPR性能 |
4 结论
UFMC的高PAPR问题限制了它在未来5G以及IoT和M2M通信中的应用。在本文中, 通过子带映射的方法将SLM和UFMC有效结合, 一种基于选择映射的通用滤波多载波系统被提出。仿真结果表明SLM-UFMC可以有效地降低UFMC的PAPR, 而且增大候选子带个数U, 可以进一步提高系统性能。同时, SLM-UFMC的PAPR性能也和载波数密切相关。载波数越多, 系统性能越差。由于SLM-UFMC仅改变了信源的统计特性并不改变发送信号的幅值, 因此SLM-UFMC并没有提高UFMC的误码率。本文主要研究了SLM-UFMC的PAPR问题, 对于如何进一步提高其误码率性能也是一个值得深入探究的课题。
References
- You Xiaohu, Pan Zhiwen, Gao Xiqi, et al. The 5G Mobile Communication:the Development Trends and Its Emerging Key Techniques[J]. Science China Information Sciences, 2014, 44(5): 551–563 [Article] (in Chinese) [Google Scholar]
- Shafi M, Molisch A F, Smith P J, et al. 5G:A Tutorial Overview of Standards, Trials, Challenges, Deployment, and Practice[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(6): 1201–1221 [Article] [CrossRef] [Google Scholar]
- SCHAICH F, WILD T. Waveform Contenders for 5G-OFDM vs. FBMC vs. UFMC[C]//6th International Symposium on Communications, Control and Signal Processing, New York, 2014 [Google Scholar]
- Na D, Choi K. Low PAPR FBMC[J]. IEEE Trans on Wireless Communications, 2017, 17(1): 182–193 [Article] [CrossRef] [Google Scholar]
- Farhang A, Marchetti N, Doyle L E. Low-Complexity Modem Design for GFDM[J]. IEEE Trans on Signal Processing, 2015, 64(6): 1507–1518 [NASA ADS] [CrossRef] [Google Scholar]
- VAKILIAN V, WILD T, SCHAICH F, et al. Universal-Filtered Multi-Carrier Technique for Wireless Systems Beyond LTE[C]//IEEE Globecom Workshops, 2013: 223–228 [Google Scholar]
- Han S H, Lee J H. An Overview of Peak-to-Average Power Ratio Reduction Techniques for Multicarrier Transmission[J]. IEEE Wireless Communications, 2005, 12(2): 56–65 [Article] [CrossRef] [Google Scholar]
- Rong W, Cai J, Yu X. Low-Complexity PTS PAPR Reduction Scheme for UFMC Systems[J]. Cluster Computing, 2017, 20(4): 3427–3440 [Article] [CrossRef] [Google Scholar]
- Tani K, Medjahdi Y, Shaiek H, et al. PAPR Reduction of Post-OFDM Waveforms Contenders for 5G & Beyond Using SLM and TR Algorithms[C]//25th International Conference on Telecommunications, 2018 [Google Scholar]
- Wei S, Li H, Zhang W, et al. A Comprehensive Performance Evaluation of Universal Filtered Multi-Carrier Technique[J]. IEEE Access, 2019, 7: 81429–81440 [Article] [CrossRef] [Google Scholar]
- Wu M, Dang J, Zhang Z, et al. An Advanced Receiver for Universal Filtered Multicarrier[J]. IEEE Trans on Vehicular Technology, 2018, 67(8): 7779–7783 [Article] [CrossRef] [Google Scholar]
All Figures
 |
图1 通用滤波多载波系统典型结构图 |
| In the text | |
 |
图2 基于选择映射的通用滤波多载波系统框图 |
| In the text | |
 |
图3 N=512时, OFDM、UFMC、SLM-OFDM和SLM-UFMC系统PAPR性能对比 |
| In the text | |
 |
图4 N=128时, OFDM、UFMC、SLM-OFDM和SLM-UFMC系统PAPR性能对比 |
| In the text | |
 |
图5 不同候选子带个数下SLM-UFMC PAPR性能 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


