| Issue |
JNWPU
Volume 38, Number 1, February 2020
|
|
|---|---|---|
| Page(s) | 183 - 190 | |
| DOI | https://doi.org/10.1051/jnwpu/20203810183 | |
| Published online | 12 May 2020 | |
Obstacle Avoidance Path Planning of Space Redundant Manipulator Based on a Collision Detection Algorithm
基于碰撞检测的空间冗余机械臂避障路径规划
1
School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China
2
National Key Laboratory of Aerospace Flight Dynamics, Xi'an 710072, China
Received:
28
February
2019
This paper focuses on the path planning of free-floating space redundant manipulator in an environment with obstacles. Firstly, based on the idea of spherical bounding volume and spatial superposition, the spatial occupying relationship between obstacles and manipulators is described in a simpler way. Then the relative position relationship between straight line segment and sphere is used to judge whether a collision between the manipulator and the obstacle. With the principle of forward kinematics, we use the joint parameterization method to transform the path planning problem into a parameter optimization problem with constraints. In this optimization problem, the objective function is a weighted optimization objective function, which includes two terms, the first term describes the base attitude disturbance and the second one is established according to the requirement of avoidance collision. The motion trajectories of the manipulator joints can be obtained by solving the optimization problem using the particle swarm optimization algorithm. We choose a 7-DOF space redundant manipulator for simulation study, and simulation results show the effectiveness of the proposed method, there is no collision between the manipulator and obstacles, and there is no disturbance on the base attitude. What's more, the trajectory of the joint is smooth, which can make the end-effector reach the desired pose with a high accuracy.
摘要
针对障碍环境中自由漂浮模式空间冗余机械臂的路径规划问题进行了研究。首先基于球形包围盒和空间叠加思想简化描述障碍物和机械臂的空间占位关系,采用直线段与球体之间相对位置关系判断是否碰撞的检测方法。然后从正向运动学出发,运用关节参数化方法,把路径规划问题变为带约束的参数优化问题,并考虑基座姿态扰动最小以及碰撞规避建立多项加权的目标函数,通过粒子群优化算法求解最优解,得到机械臂关节运动轨迹。最后以七自由度空间冗余机械臂为例进行仿真,结果表明该方法可以实现有效避障,同时基座姿态受扰很小,关节运动轨迹平滑,且机械臂末端也能够以较高精度达到期望位姿。
Key words: space redundant manipulator / collision detection algorithm / obstacle avoidance path planning / particle swarm optimization / spherical bounding volume / spatial superposition / simulation / motion trajectory
关键字 : 空间冗余机械臂 / 碰撞检测算法 / 避障路径规划 / 粒子群优化算法 / 球形包围盒 / 空间叠加 / 数值仿真 / 运动规划
© 2020 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
随着航空航天技术的飞速发展, 空间机器人凭借其具有在复杂环境下执行卫星零件组装、空间目标捕获与在轨维护等高难度操作任务的能力, 在空间探索及在轨服务中发挥着重要作用。对于空间冗余机械臂系统, 针对给定的操作任务, 路径规划是首先需要解决的问题[1]。当考虑自由漂浮模式的时候, 空间机械臂系统角动量不可积, 整个系统具有非完整特性, 此时即使各个关节角运动相同, 但当选取不同的闭合路径时, 机械臂末端位姿也会不相同。另外, 空间机械臂系统的广义雅克比矩阵不仅与运动学参数有关, 还与动力学参数密切相关, 求解过程中会产生动力学奇异。因此, 由于非完整约束特性和动力学奇异特性, 致使自由漂浮空间机械臂的路径规划非常复杂[2]。此外, 实际操作过程中, 机械臂工作空间内可能会有障碍物的存在, 例如空间碎片、空间舱体外设试验装置、外接桁架结构、天线、太阳帆板等, 这些都会阻碍机械臂末端到达给定目标点, 这就需要能够规划出一条安全的无碰撞的机械臂运动轨迹。因此, 研究自由漂浮空间机械臂系统的避障规划问题具有重要意义。
对于自由漂浮空间机器人动力学奇异回避路径规划问题, 目前主要有3类解决方法, 分别是奇异点消除法[3-4]、奇异问题转化法[5-6]、回避奇异点路径法[7-8], 都可以有效实现动力学奇异回避, 但是研究这类问题的时候基本都没有考虑避障问题。也有不少学者对机械臂避障规划问题进行了研究, 采用的方法大体可以分为3大类:几何模型法、人工势场法、多项式插值。几何模型法主要有A*算法、快速扩展随机树、C空间法等。A*算法[9-10]是一种全局最优规划算法, 但其所需要的场景信息很多, 计算量巨大, 而且一般规划出的路径也并非最优。快速扩展随机数法[11]适用于多自由度轨迹规划, 它是一种基于随机采样的步进式算法, 但该方法存在重复性不好、规划的路径不光滑、规划器参数调整困难、缺乏对算法系统性的理论分析等不足。C空间法[12-13]主要思想是将机械臂工作空间分为障碍空间和自由空间2个子空间, 然后利用启发式搜索算法在机械臂自由空间内寻找一条无碰撞路径, 但对于新的工作环境需要重新构建C空间, 难以满足机械臂运动实时性和通用性的要求。人工势场法[14-15]是可应用于各个领域的一种避障方法, 但是其搜索量大, 而且当笛卡尔空间中引力和斥力场较多时, 某些区域受到多个势点作用, 产生局部极小值, 容易出现奇异点。多项式插值法[16]主要采用寻找中间点的方法以保证末端执行器避开障碍物, 但未将关节和连杆避障情况考虑其中。以上这些规划方法虽然可以实现机械臂避障规划, 但各有不足, 而且所得规划结果未必最优。
为此, 本文针对自由漂浮空间冗余机械臂系统, 研究避免动力学奇异的避障路径规划问题。首先将机械臂连杆约束考虑在内, 通过对障碍物以及连杆空间占位关系进行简化描述, 设计避障检测算法。在此基础上, 利用正向运动学方法进行动力学奇异规避, 采用正弦多项式对机械臂关节进行参数化, 结合避障检测算法, 把路径规划问题转变为带约束的参数优化问题。然后利用粒子群优化算法进行求解, 得到冗余机械臂最优避障路径。
1 避障规划建模
1.1 空间机械臂运动学模型
图 1给出了n自由度的自由漂浮基座空间机器人的示意图, 其中末端执行器与第n个关节固连。
图中B0表示自由漂浮基座; Bi(i=1, 2, …, n)表示机械臂的第i个连杆; Ji(i=1, 2, …, n)表示连杆Bi-1和Bi之间的旋转关节; CM, Ci分别表示整个空间冗余机械臂系统的质心与连杆Bi的质心; OI, Oi分别表示惯性坐标系原点与第i个连杆坐标系原点; ri∈R3表示惯性坐标系原点到Bi质心的位置矢量; pi∈R3表示惯性坐标系原点到Ji的位置矢量; pe∈R3表示惯性坐标系原点到末端执行器的位置矢量; ai, bi∈R3分别表示从Ji指向Ci,Ci指向Ji+1的矢量。ki为第i个关节轴旋转方向上的单位矢量。
空间机器人系统的一般运动学方程为[17]
式中:ve, ωe分别表示机械臂末端的线速度和角速度; v0, ω0分别表示基座的线速度和角速度; vi, ωi分别表示各机械臂的线速度和角速度; 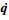 (q=[q1,q2, …,qn]T)表示机械臂关节角速度向量。
(q=[q1,q2, …,qn]T)表示机械臂关节角速度向量。
考虑到在机械臂的轨迹规划中, 空间冗余机械臂系一般采用关节角变量作为系统的状态变量, 则需要将(1)式中基座的角速度与线速度用关节角表示出来。而对于自由漂浮空间机器人, 其基座姿态和位置都不受控, 则利用线动量和角动量守恒, 经推导可以得到如下运动学模型[17]
式中:Jg=JbJbm+Jm, Jbm与Jb形式相似, 具体表达式参见参考文献[17]。
(2) 式用广义雅可比矩阵Jg把机械臂末端的线速度和角速度与机械臂关节角联系起来, 广义雅可比矩阵Jg不只与运动学参数有关, 而且与动力学参数相关, 它是基座姿态、各关节转向、各刚体质量惯量等的综合函数, 具有非常强的耦合特性。
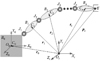 |
图 1 自由漂浮空间机器人的示意图 |
1.2 碰撞检测算法
避障路径规划需要建立碰撞检测算法, 以判断是否碰撞, 例如文献[18]采用了将机械臂连杆与障碍物2个不规则实体之间的碰撞检测简化成了直线段与球体之间位置关系的判断, 但是没有考虑机械臂的直径。文献[19]基于障碍物伪距离技术, 采用自由漂浮空间机器人的逆几何模型求解期望末端位姿下的连杆伪距离估计值, 以判断是否碰撞。文献[20]针对旋转目标, 以杆件最近距离为约束条件, 研究了漂浮空间机器人的避障控制方法。因此碰撞检测算法设计是进行空间冗余机械臂系统避障规划的前提。
1.2.1 机械臂及障碍物空间占位关系的简化描述
本文研究对象是七自由度空间冗余机械臂, 一般情况下, 机械臂连杆大多类似为长方体或圆柱体, 使得机械臂与障碍物2个不规则实体之间的碰撞检测关系十分复杂。为了便于计算, 本文基于球形包围盒和空间叠加的思想, 对障碍物和机械臂的空间占位关系进行简化描述。通过将机械臂连杆的径向最大球形包围盒半径叠加到障碍物的厚度上, 将机械臂连杆和障碍物2个实体之间复杂的空间占位关系转变成了直线段和实体之间的相对位置关系, 如图 2所示。虽然会造成机械臂一部分工作空间的浪费, 但却极大地简化了机械臂和障碍物的空间占位关系, 有利于进行碰撞的判定和检测, 提高避障的可靠性。
另外, 对于空间中的三维障碍物, 可能具有不规则的几何形状, 空间占位描述复杂, 给碰撞检测带来很大的困难。为此本文采用障碍物的规则体包围盒对其空间占位进行简化描述, 这种方法虽然在一定程度上扩大了障碍物空间占位范围, 但是能够极大地简化碰撞检测过程, 从而使得避障路径规划的效率得到大幅提升, 同时也能够使得整个机械臂避障路径规划的安全性进一步增加。
一般常用的包围盒方式有球形包围盒、六面体包围盒[21], 本文的研究中采用球形包围盒来对障碍物的空间占位进行描述。定义障碍物包围球为可以完全包住障碍物的最小球体。一般选取障碍物上距离最远两点之间的连线当作包围球的直径, 其表达式如下[22]
式中:(a, b, c)为包围球的中心坐标; r为包围球半径; (x, y, z)为障碍物表面任意一点的坐标。这种球形包围盒的描述方法, 简单直观, 方便计算, 使后续的碰撞检测变得容易。
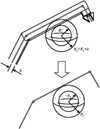 |
图 2 机械臂连杆简化过程示意图 |
1.2.2 碰撞检测算法
基于机械臂连杆与障碍物2个不规则实体之间的空间占位关系的简化描述, 可以利用直线段和实体之间的相对位置关系, 进行碰撞检测算法的设计。值得注意的是, 包围球与机械臂的碰撞判断不仅要考虑包围球与机械臂连杆的最小垂直距离, 更要考虑其垂足在机械臂连杆上的相对位置。
设t为比例系数, 表示包围球中心在机械臂连杆上的垂足与机械臂关节的距离占机械臂长度的比例, A, B为机械臂关节点坐标, O为障碍物中心的坐标, C为O点到机械臂连杆AB的垂足。通过垂直关系
得
利用‖lAB‖, t和‖lOC‖的运算关系将包围球与机械臂的碰撞检测分为以下4种情况:
1) 连杆AB到障碍物中心O的距离大于包围球的半径(‖lOC‖>r), 此时机械臂与障碍物不发生碰撞, 如图 3a)所示。
2) 连杆AB到障碍物中心O的距离小于包围球的半径(‖lOC‖ < r), 但垂足C点位于连杆AB的延长线上, 且与包围球不相交, 即t < 0且(‖lAB‖*‖t‖)2+‖lOC‖2>r2; 或t>1且(‖lAB‖*‖t-1‖)2+‖lOC‖2>r2。此时机械臂与障碍物不发生碰撞, 如图 3b)所示。
3) 连杆AB到障碍物中心O的距离小于等于包围球的半径(‖lOC‖≤r), 且与包围球交点有2个交点, 即‖lOC‖≤r且0 < t < 1。此时机械臂与障碍物发生碰撞, 如图 3c)所示。
4) 连杆AB到障碍物中心O的距离小于包围球的半径(‖lOC‖ < r), 但垂足C点位于连杆AB的延长线上, 且与包围球交点有一个交点, 即t < 0且(‖lAB‖*‖t‖)2+‖lOC‖2≤r2; 或t>1且(‖lAB‖*‖t-1‖)2+‖lOC‖2≤r2。此时机械臂与障碍物发生碰撞, 如图 3d)所示。
根据图 3中对直线段与球体的位置关系分析, 于是就很容易进行机械臂连杆与障碍物的碰撞检测。
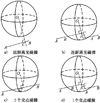 |
图 3 机械臂与障碍物碰撞检测判断示意图 |
2 基于粒子群优化的冗余机械臂避障路径规划
空间机器人的路径规划是指规划各关节的运动, 使末端执行器能够从初始状态到达目标状态。即对于系统的运动学方程(2), 求解关节角q=[q1, q2, …, qn]T的变化规律, 在规定时间内, 使得系统末端执行器的位置和姿态从初始状态运动到达目标状态。若已知末端执行器的期望运动规律, 则通过对(2)式进行逆运动学求解, 可以得到关节角q=[q1, q2, …, qn]T的变化规律。但是, 当Jg不可逆时, 出现动力学奇异问题。为了避免该问题, 可以采用正运动学求解方法, 通过设定关节角q, 使其满足上式。
为此, 本文采用正运动学方法进行求解, 基于多项式拟合的方法, 通过设定各个关节角q, 将机械臂的逆运动学规划问题转化为正运动学参数优化问题进行求解。
假设机械臂第i个关节角qi(i=1…n)的变化规律如下[23]
式中:bi0, bi1, bi2和bi3是参数化多项式的系数, 为待定参数, Δi为关节Ji的角度限制。对(7)式进行求导得到机械臂相应的关节角速度和角加速度如下
一般情况下, 令初始时刻和终端时刻所有关节的角速率均为零, 且初始时刻的关节角大小已知, 如下所示
将边界条件(10)式代入到(7)至(9)式中, 得
从(11)式可以看出, 关节角多项式的系数只包含bi3, 因此, 只要求出参数bi3就能够根据(7)至(9)式进行相应的轨迹规划。
自由漂浮模式空间冗余机械臂基座的位置与姿态均不受控制, 因此规划过程中机械臂与基座会产生耦合效应, 这在一定程度上会影响任务规划的精度。为了实现基座姿态无扰, 本节待优化的目标函数取为机械臂运动过程中对基座姿态干扰最小, 目标函数如下所示
系统应满足边界约束
式中:qb表示空间冗余机械臂基座的姿态角; ‖·‖表示二范数; ref表示机械臂末端执行器终止时刻的末端期望位置; ψef表示机械臂末端执行器终止时刻的末端期望姿态。
除此之外, 整个系统还要满足机械臂连杆的避障约束, 将避障约束以罚函数的形式添加到目标函数之中, 即
式中:λ为惩罚因子; fob为罚函数项, 定义如下
式中:r表示障碍物的包围球半径; d表示机械臂连杆(直线段)到包围球球心的最短距离。
此时, 空间冗余机械臂的避障路径规划问题就转变为目标优化问题, 利用相应的优化算法求解出使目标函数函数J2最小, 且同时满足边界约束条件(13)式的参数bi3(i=1, 2, 3, …, n), 就可以根据(11)式计算bi0, bi1, bi2。
考虑到PSO算法优越的性能, 且不少学者已成功利用PSO算法进行了机器人的运动规划, 因此, 本文也利用PSO算法进行机械臂避障运动规划问题的求解, 得到优化参数bi0, bi1, bi2, bi3之后, 再根据(7)至(9)式计算优化后的关节轨迹及其变化规律。
3 仿真结果与分析
本文以一个具有七关节的空间冗余机械臂为仿真对象, 其各项参数如表 1所示。
机械臂各关节初始状态
机械臂基座初始姿态
机械臂末端执行器的期望位姿
关节角大小, 角速度大小和角加速度的大小限制为qmax=270°, qmin=-270°,  max=5°/s,
max=5°/s,  min=-5°/s,
min=-5°/s,  max=0.5°/s2,
max=0.5°/s2,  min=-0.5°/s2。
min=-0.5°/s2。
为验证碰撞检测算法的有效性, 取前期优化得到机械臂末端必经点(-1.95, 4.96, 7.87)T为障碍物中心O的位置。优化所需仿真参数为:tf=30s, 粒子数N=40, 迭代最大数为200, 惩罚因子λ=10。
使用MATLAB进行仿真, 结果如图 4至9所示。其中图 4表示空间冗余机械臂末端执行器的运行路线, 其中图 4a)是不考虑障碍物的情况, 图 4b)是考虑障碍物并进行避障的情况。从图中可以看出, 在有障碍物的情况下, 机械臂末端执行器在运动过程中有效地避开了障碍物, 并达到了指定的目标点, 实现了空间冗余机械臂的避障路径规划。
图 5表示的是空间冗余机械臂避障路径过程中基座的姿态变化曲线, 从图中可以看出整个规划过程中, 基座姿态扰动控制在10-3数量级, 实现了基座姿态无扰的目标, 图 6是机械臂末端执行器的姿态变化曲线, 图 7至9分别为空间冗余机械臂各关节角度、角速度以及角加速度变化曲线, 从图中可以看出, 整个避障规划过程关节变化平缓, 且满足各关节角、关节角速度以及关节角加速度的限制, 是一种简单有效的避障路径规划方法。
7自由度空间冗余机械臂各结构参数
 |
图 4 空间冗余机械臂路径规划过程 |
 |
图 5 基座姿态角变化曲线 |
 |
图 6 末端执行器姿态变化曲线 |
 |
图 7 机械臂各关节角变化曲线 |
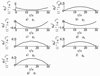 |
图 8 机械臂各关节角速度变化曲线 |
 |
图 9 机械臂各关节角加速度变化曲线 |
4 结论
针对障碍环境中的自由漂浮空间冗余机械臂避障运动规划问题, 本文研究表明:
1) 可以通过对机械臂连杆及障碍物2个不规则实体之间的复杂空间占位的简化, 设定碰撞检测算法。
2) 利用运动学方法和多项式参数化方法, 既可以实现动力学奇异规避, 同时也可以实现机械臂的有效避障路径规划。
References
- Flores-Abad A, Ma O, Pham K, et al. A Review of Space Robotics Technologies for On-Orbit Servicing[J]. Progress in Aerospace Sciences, 2014, 68(8): 1–26 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Xu W F, Zhang J T, Qian H H, et al. Identifying the Singularity Conditions of Canadarm2 Based on Elementary Jacobian Transformation[C]//IEEE International Conference on Intelligent Robots and Systems, Tokyo, 2013: 795–800 [Google Scholar]
- Nakamura Y, Hanafusa H. Inverse Kinematic Solutions with Singularity Robustness for Robot Manipulator Control[J]. Journal of Dynamic Systems, Measurement and Control, Transactions of the ASME, 1986, 108(3):163–171 [Article] [CrossRef] [Google Scholar]
- Xu Wenfu, Liang Bin, Liu Yu, et al. A Novel Approach to Avoid Singularities of PUMA-Type Manipulators[J]. Acta Automatica Sinica, 2008, 34(6):670–675 [Article] (in Chinese) [Google Scholar]
- Nenchev D, Umentani Y, Yoshida K. Analysis of a Redundant Free-Flying Spacecraft/Manipulator System[J]. IEEE Trans on Robotics and Automation, 1992, 8(1): 1–6 [Article] [CrossRef] [Google Scholar]
- Zhang Fuhai, Fu Yili, Wang Shuguo. Trajectory Planning of Free-Floating Space Robot with Avoidance of Dynamic Singularity[J]. Robot, 2012, 34(1): 38–43 [Article] (in Chinese) [CrossRef] [Google Scholar]
- Papadopoulos E, Dubowsky S. Dynamic Singularities in Free-Floating Space Manipulators[J]. Journal of Dynamic Systems, Measurement and Control, Transactions of the ASME, 1993, 115(1): 44–52 [Article] [CrossRef] [Google Scholar]
- Nanos K, Papadopoulos E. On Cartesian Motions with Singularities Avoidance for Free-Floating Space Robots[C]//IEEE International Conference on Robotics and Automation, Saint Paul, 2012: 5398–5403 [Article] [Google Scholar]
- Zhao Zhenming, Meng Zhengda. Path Planning of Service Mobile Robot Based on Adding-Weight A* Algorithm[J]. Journal of Huazhong University of Science and Technology, 2008(suppl 1):196–198 [Article] (in Chinese) [Google Scholar]
- Jia Qingxuan, Chen Gang, Sun Hanxu, et al. Path Planning for Space Manipulator to Avoid Obstacle Based on A* Algorithm[J]. Journal of Mechanical Engineering, 2010, 46(13):109–115 [Article] (in Chinese) [Google Scholar]
- Xie Biyun, Zhao Jing, Liu Yu. Motion Planning of Reaching Point Movements for 7R Robotic Manipulators in Obstacle Environment Based on Rapidly-exploring Random Tree Algorithm[J]. Journal of Mechanical Engineering, 2012, 48(3):63–69 [Article] (in Chinese) [Google Scholar]
- Wang Yue, Jia Yinghong, Xu Shijie. Collision-Free Motion Planning Algorithm for Redundant Space Manipulators during Coarse Target Capturing[J]. Chinese Space Science and Technology, 2012, 6(3): 49–55 [Article] (in Chinese) [Google Scholar]
- Fiorini P, Shiller Z. Motion Planning in Dynamic Environments Using the Relative Velocity Paradigm[C]//IEEE International Conference on Robotics and Automation, Atlanta, 1993: 560–566 [Article] [Google Scholar]
- Park M, Jeon J, Lee M. Obstacle Avoidance for Mobile Robots Using Artificial Potential Field Approach with Simulated Annealing[J]. IEEE International Symposium on Industrial Electronics, 2001(3): 1530–1535 [Article] [Google Scholar]
- Liu S, Zhang Q, Zhou D. Obstacle Avoidance Path Planning of Space Manipulator Based on Improved Artificial Potential Field Method[J]. Journal of The Institution of Engineers: Series C, 2014, 95(1): 31–39 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Shi Zhong, Wang Yongzhi, Hu Qinglei. A Polynomial Interpolation Based Particle Swarm Optimization Algorithm for Trajectory Planning of Free-Floating Space Robot[J]. Journal of Astronautics, 2011, 32(7): 1516–1521 [Article] (in Chinese) [Google Scholar]
- Kevin M L, Frank C P. Modern Robotics Mechanics, Planning, and Control[M]. Cambridge:Cambridge University Press, 2017 [Google Scholar]
- Lyu Shun. Collision Avoidance Path Planning of Free-floating Space Robot[D]. Xi'an: Northwestern Polytechnical University, 2015 (in Chinese) [Google Scholar]
- Yang Fan, Zhang Guoliang, Tian Qi, et al. Trajectory Planning-Tracking Integrated Control for a 6R Free-Floating Space Robot via Obstacle Avoidance Pseudo-Distance[J]. Journal of Astronautics, 2018, 39(2): 229–237 [Article] (in Chinese) [Google Scholar]
- Wang M M, Luo J J, Walter U. A Non-linear Model Predictive Controller with Obstacle Avoidance for a Space Robot[J]. Advances in Space Research, 2016, 57(8): 1737–1746 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard P M. Collision Detection for Interactive Graphics Applications[J]. IEEE Trans on Visualization Computer Graphics, 1995, 1(3): 218–230 [Article] [CrossRef] [Google Scholar]
- Webster N. Webster's New Universal Unabridged Dictionary[M]. New York: Dilithium Press, 1989: 1–2 [Google Scholar]
- Liu X, Baoyin H, MA X. Optimal Path Planning of Redundant Free-Floating Revolute-Jointed Space Manipulators with Seven Links[J]. Multibody System Dynamics, 2013, 29(1): 41–56 [Article] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
图 1 自由漂浮空间机器人的示意图 |
| In the text | |
 |
图 2 机械臂连杆简化过程示意图 |
| In the text | |
 |
图 3 机械臂与障碍物碰撞检测判断示意图 |
| In the text | |
 |
图 4 空间冗余机械臂路径规划过程 |
| In the text | |
 |
图 5 基座姿态角变化曲线 |
| In the text | |
 |
图 6 末端执行器姿态变化曲线 |
| In the text | |
 |
图 7 机械臂各关节角变化曲线 |
| In the text | |
 |
图 8 机械臂各关节角速度变化曲线 |
| In the text | |
 |
图 9 机械臂各关节角加速度变化曲线 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


