| Issue |
JNWPU
Volume 39, Number 2, April 2021
|
|
|---|---|---|
| Page(s) | 326 - 333 | |
| DOI | https://doi.org/10.1051/jnwpu/20213920326 | |
| Published online | 09 June 2021 | |
Probabilistic fatigue life prediction of metallic components based on continuum damage mechanics
基于损伤力学的金属构件概率疲劳寿命预测方法
1
School of Aeronautical Engineering, Zhengzhou University of Aeronautics, Zhengzhou 450046, China
2
Research Institute of Unmanned Aerial Vehicles, Zhengzhou University of Aeronautics, Zhengzhou 450046, China
3
School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China
Received:
22
June
2020
Based on continuum damage mechanics, a probabilistic method of predicting high-cycle fatigue life for metallic components is proposed. First, macro-meso two-scale stress-strain equations are established by combining Eshelby-Kroner localization law and classic elastic-plastic constitutive equation. Second, some parameters in Lemaitre's fatigue damage evolution model are randomized. Probabilistic properties of which are obtained by inverse-analysis and optimization. Then, the probabilistic method of predicting high-cycle fatigue life is established by coupling the model with macro-meso two-scale equations. And the proposed algorithm is coded with Fortran language, which is non-intrusive post-program of FEM analysis. Next, constant amplitude fatigue test of Al 2024-T3 coupon is performed to determine probabilistic properties of model parameters. Finally, as the object of study, wallboard is analyzed by FEM. Taking skin-strip component as research object, the fatigue life of hot spot is predicted by proposed method. The corresponding fatigue test of the component is performed, which verifies the effectiveness of proposed method to predict probabilistic life of metallic components.
摘要
基于连续介质损伤力学，提出了一种预测金属构件高周疲劳寿命的概率方法。结合Eshelby-Kroner局域化准则和金属典型弹塑性本构方程构建了宏细观双尺度应力应变桥联方程；将Lemaitre疲劳损伤演化模型中部分参数随机化，通过对模型反演优化获取其概率特性。结合双尺度桥联方程和疲劳损伤演化概率模型建立了预测高周疲劳寿命的概率方法，通过Fortran编程实现新算法，作为有限元分析的非嵌入后处理程序。完成了铝合金2024-T3光滑圆棒常幅谱疲劳实验，从而确定模型参数概率特性，以某型飞机蒙皮-带板搭接壁板为研究对象，利用新方法预测其危险点概率疲劳寿命，并完成了相应疲劳实验，验证了新方法预测金属构件概率疲劳寿命的有效性。
Key words: continuum damage mechanics / high-cycle fatigue / probabilistic property / aluminum alloy / life prediction / Lemaitre model / fatigue test / FEM analysis
关键字 : 损伤力学 / 疲劳 / 概率特性 / 铝合金
© 2021 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
金属材料广泛应用于工程领域中，如航空、航海和汽车等领域。疲劳失效是金属构件最常见的一种失效形式，美国土木工程师协会(ASCE)研究表明金属构件80%~90%的失效都与疲劳有关[1]。随着现代工程结构对总体性能要求的不断提高，结构构件不断向精细化设计和整体化制造发展，这使结构疲劳问题越来越突出。另外，疲劳寿命存在很大的分散性，尤其是对于高周疲劳，使得在结构可靠性安全寿命设计过程中存在很大的难题。工程上对于疲劳寿命预测的研究主要是通过标准件疲劳实验建立应力、应变及能量和确定性寿命(中值寿命或某一可靠度下的寿命)的关系，如S-N曲线、ε-N曲线和Darvaeux模型等。确定性寿命不能充分反映疲劳寿命的概率统计特征，如概率分布类型及标准差、峰度和偏度等，概率疲劳寿命应能表征其概率分布和相应的分布参数。目前，多数研究是基于这些模型的改进，如白恩军等[2]将不同级应力水平的疲劳寿命等效到最高级应力水平，实现了小样本下p-S-N曲线的拟合。刘红彬等[3]通过改进的平均应力公式预测了涡轮盘螺栓孔处的疲劳寿命。罗媛等[4]基于S-N曲线与Miner准则，构建了桥梁疲劳损伤的功能函数，用于简支梁桥的疲劳可靠度评估。马玉娥等[5]通过玻璃纤维铝合金层板(FMLs)疲劳实验建立了S-N曲线，为其疲劳寿命预测提供了材料基础性能和信息。Doudard等[6]在最弱连接理论框架下提出一种概率双尺度模型，用于预测S-N曲线的分散性。
上述方法相对简单易用，但对于变幅加载下的复杂工程构件，需结合损伤累积准则预测疲劳寿命[7]，且预测结果通常偏差较大，在工程应用上有一定局限性[8]。近年来，疲劳损伤形成和演化机理成为国内外学者的研究重点之一，连续介质损伤力学(continuum damage mechanics, CDM)[9]在此背景下逐渐发展成熟。Lemaitre等[10]基于损伤力学发展出一套疲劳损伤演化模型用于确定性疲劳寿命预测，但目前仍鲜见有基于损伤力学的概率疲劳寿命预测方法。本文旨在采用金属材料双尺度局域化准则和严谨的连续介质损伤力学理论，将Lemaitre疲劳损伤演化模型参数概率化，针对金属构件，建立预测高周疲劳寿命的概率方法。
1 双尺度疲劳损伤演化概率模型
由于高周疲劳宏观无塑性，本节将首先建立宏细观双尺度桥联方程，用于计算细观应力应变场，作为Lemaitre疲劳损伤演化模型的输入，并将模型概率化，建立预测金属构件高周概率疲劳寿命的算法流程。
1.1 宏细观双尺度桥联方程
基于Eshelby-Kroner局域化准则和损伤演化模型，Lemaitre等[10]于1999年提出了一种双尺度疲劳损伤演化模型，可以有效预测金属材料高周疲劳寿命。本节将对其进行简要介绍。
由于材料中存在各种缺陷, 疲劳损伤演化的微观机理极其复杂, 而微观尺度下大量微观缺陷的力学特性无法直接表征。微观缺陷总是劣化或减弱材料的力学性能, 从均匀化的力学角度出发, Eshelby-Kroner局域化准则将这些缺陷统一看作细观尺度下RVE内的一个弱夹杂, 再通过弱夹杂的力学行为分析损伤演化, 如图 1所示, 其中上标μ表示细观尺度下的变量, 后文均代表此意义。
其中, 联系宏细观应力应变的方程如(1)式所示
(1) 式也称为Eshelby-Kroner局域化方程[11], 式中:
结合Eshelby-Kroner局域化方程和经典弹塑性本构方程, 可得求解细观应力应变的方程组, 其矢量表达如(3)式所示
式中: σμ, εμe和εμp是未知的细观应力、弹性应变和塑性应变; fμ是屈服函数; Xμ是随动强化背应力; Rμ是由于等向强化引起的屈服面半径的增量; Dμe是弹性模量; σ, ε和εp是已知的宏观应力、总应变和塑性应变。
对于实际工程构件, 需首先通过有限元分析其在载荷谱作用下的危险点宏观应力应变场序列, 作为(3)式的初始输入。为求解细观应力应变场序列, 由于其细观进入塑性, 因此需采用隐式迭代求解算法, 包括弹性预测和塑性修正, 算法流程如图 2所示。
 |
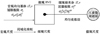图 1 Eshelby-Kroner局域化准则 |
 |
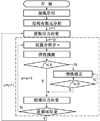图 2 宏细观双尺度桥联模型隐格式求解算法流程框图 |
1.2 疲劳损伤演化模型及其概率化算法
基于细观应力应变场序列, 可代入Lemaitre疲劳损伤演化模型计算高周疲劳损伤累积, 如下
式中: Ḋ为损伤演化率; pμ为细观等效塑性应变; pD为损伤累积门槛值; Dc为疲劳损伤临界值; S和s为损伤演化参数; Yμ为损伤能量释放率, 表达式如(5)式
式中: σeqμ是von Mises等效应力; σmμ是平均球应力; E是弹性模量; ν是泊松比; Rvμ应力三轴度函数。
本文将按照Lemaitre文献对模型进行一些简化[10]: 忽略损伤和弹塑性本构方程的耦合; 疲劳损伤门槛值pD=0, 意味着进入塑性即发生损伤; 疲劳损伤临界值Dc=1;仅考虑材料随动强化, 且细观随动强化参数与宏观一致。模型参数E, ν, σ和C可通过材料静力拉伸实验或查手册获得, 对于金属材料, 局域化方程参数α通常取为0.4, 此时仅剩S和s未知, 因此疲劳寿命N是关于S和s的函数
式中: 上标“+”代表上半拉伸循环；上标“-”代表下半压缩循环。
通常情况下, 模型参数可通过模型反演优化获得, 通过使模型预测寿命和实验寿命平方和最小, 建立如下优化方程
式中: Nt为疲劳实验寿命; S和s的取值范围参考文献[12], 每个实验寿命可得到1组S和s的样本值。
由于相同应力水平加载下, 疲劳寿命具有很大分散性, 因此本文认为S和s是服从某种分布的随机变量, 通过(7)式优化获得S和s样本, 首先利用EDF拟合优度检验其分布类型, 并统计样本获得其概率特性。对于金属构件承受复杂加载情况, 如多级块谱或随机谱加载, 本文方法预测其高周疲劳寿命分为以下3个步骤:
1) 通过有限元计算金属构件危险点的宏观应力应变。对于高周疲劳, 宏观应力应变处于弹性状态, 因此在弹性状态下进行一次有限元分析, 确定构件危险细节并提取其应力应变, 乘以相对于载荷谱峰谷值比例系数即可获得应力应变峰谷值序列;
2) 按双尺度桥联模型隐格式算法进行细观应力应变滞回曲线的非线性计算, 得到相应的细观应力应变峰谷值序列;
3) 对S和s进行随机抽样, 每组样本代表 1个“试件”, 通过(4)式计算构件危险点在每个载荷循环的疲劳损伤量, 并累积损伤, 记录循环数; 当D≥Dc时, 结束计算, 得到总循环数, 即疲劳寿命N的1个样本。
上述双尺度疲劳损伤演化算法通过Fortran编程实现, 其中包括宏细观双尺度应力应变计算以及疲劳损伤累积计算, 作为非嵌入后处理器来计算每个循环内累积的损伤并预测疲劳寿命。
2 实验设计及模型验证
本节设计完成了铝合金光滑圆棒在6组应力水平下的高周疲劳实验, 选取实验材料为工程中常用的铝合金2024-T3, 主要目的是通过铝合金2024-T3疲劳实验数据分别拟合得到细观尺度下损伤演化模型中的参数S和s。之后将利用双尺度疲劳损伤演化模型预测飞机翼身连接壁板疲劳寿命, 并与实验结果对比。
2.1 模型参数获取
铝合金光滑圆棒实验件如图 3所示, 实验在6组不同应力水平下进行, 应力比均为-1, 每组8个实验件, 实验机为Instron8802电液伺服万能实验机, 按照《HB 5287-96金属材料轴向加载疲劳实验方法》进行。实验结果如表 1所示。
由于实验为光滑圆棒单轴拉伸, 且6级应力水平下试件未进入塑性, 因此可通过理论计算获得各应力水平下宏观应力应变数据, 作为双尺度桥联模型的输入, 计算细观应力应变场, 进而通过(7)式反演优化获得S和s样本, 每级应力水平下将得到8组S和s样本, 对其进行关于正态分布的EDF检验[13](95%置信度下), 并统计其均值和方差, 结果如表 2所示, 表中Dn, W2和A2为EDF统计量, 具体定义可参考文献[13]。由表可知, S和s均通过关于正态分布的EDF检验, 且不同应力水平下, S和s的均值和标准差变化很小, 因此本文认为其概率特性不随外加载荷变化, 统计6组应力水平下的S和s样本, 可得S均值和标准差分别为3.050 6和0.307 0, s的均值和标准差分别为2.353 1和0.159 9。
 |
图 3 铝合金光滑圆棒疲劳实验件 |
疲劳实验结果
各级应力水平下S和s概率特性
2.2 飞机机翼连接壁板寿命预测
飞机连接壁板取自某型客机, 为蒙皮-带板搭接壁板, 通过螺栓连接, 几何形状及螺孔位置分布如图 4所示, 图中未给出螺栓具体构型。模型关于中面对称。沿对称面从内到外的三排连接螺孔的直径分别为12.7, 12.7和11.11 mm。
蒙皮和带板材料为铝合金2024-T3, 螺栓材料为30CrMnSiA。蒙皮-带板壁板常幅谱最大应力(典型截面应力)为80 MPa, 应力比R均为0.06。
 |
图 4 蒙皮-带板搭接壁板 |
2.2.1 搭接壁板有限元分析
按照图 2所示的算法流程图, 本文首先对壁板构件进行有限元分析, 获取构件危险点的应力应变场数据, 作为本文算法的初始输入。
由于壁板含多个螺栓连接, 对所有螺栓进行实体建模并设置接触计算过于繁冗, 本文在保证精度的前提下通过整体-细节2级模型计算危险点应力应变: 先通过梁单元模拟螺栓, 并通过MPC连接梁单元和螺孔实际接触受力面模拟螺栓连接, 统计分析螺栓钉传载荷及旁路载荷选取危险细节; 再切取危险细节进行精细建模, 对螺栓进行实体建模并与螺孔设置接触, 从第一步提取危险细节边界节点力施加, 保证细节建模受力状态与整体一致, 进而计算孔边危险点应力应变。
利用Abaqus有限元分析软件对搭接壁板进行建模分析, 边界条件施加与实际实验保持一致。蒙皮-带板壁板的整体有限元计算结果如图 5所示。统计钉传载荷大小, 如表 3所示, 由于钉传载荷关于对称面大小相等, 因此只给出对称面一侧螺栓钉传载荷的结果。
由表 3可知, 对于带板来说, 第一排钉传、旁路都最大, 因此最危险; 对于蒙皮来说, 第三排钉处旁路载荷最大, 虽然钉传载荷没有第一、第二排大, 但其螺栓直径较小, 因此第三排钉最危险, 又由于此处带板的边不受约束, 因此螺栓对螺孔的挤压更严重, 产生应力集中更严重。因此对于蒙皮-带板壁板, 第三排钉处的蒙皮最危险。
提取第三排钉处的局部模型, 建立相应的螺栓, 螺母与蒙皮、带板建立接触, 螺栓与螺孔建立接触。细节边界面处网格与整体模型保持一致, 以便施加相应节点力, 且孔边网格要足够细。提取整体模型危险细节边界面上的节点力, 施加到细节模型上, 并约束任一单元以消除刚体位移。有限元计算结果如图 6所示, 可以看出带板和蒙皮危险点均在孔边, 且都未进入塑性, 而蒙皮孔边最大应力大于带板孔边最大应力, 说明蒙皮孔边最危险, 与整体有限元分析结果一致。
由有限元分析结果分别提取蒙皮危险点处的应力应变, 乘以相应系数得到实验常幅谱应力应变峰谷值序列, 作为双尺度疲劳损伤演化模型非嵌入后处理程序的输入, 计算得到细观应力应变曲线, 如图 7所示。本文对模型参数S和s抽取5 000组样本, 进而利用宏细观双尺度损伤演化模型计算得到5 000个疲劳寿命样本, 在此基础上计算疲劳寿命概率分布参数, 结果如表 4所示。
 |
图 5 蒙皮-带板整体有限元计算结果 |
蒙皮-带板钉传载荷 N
 |
图 6 蒙皮-带板细节模型计算结果 |
 |
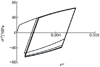图 7 搭接壁板危险点细观应力应变滞回环 |
疲劳寿命概率分布参数
2.2.2 搭接壁板疲劳实验验证
本文完成了蒙皮-带板搭接壁板试件的常幅谱疲劳实验, 试件数量为8。加载水平与有限元分析一致, 应力比为0.06, 实验在Instron8802电液伺服疲劳实验机上进行, 搭接壁板疲劳破坏位置如图 8所示。
由图 8可知, 蒙皮-带板试件疲劳破坏位置为蒙皮第三排螺孔处, 与本文前述有限元分析预测的破坏位置相同。实验疲劳寿命均值和标准差如表 5所示, 对比表 4, 对于蒙皮-带板试件, 本文方法预测寿命均值相对误差为-8.70%, 标准差相对误差为-13.47%, 均处于工程可接受范围内。
假设疲劳寿命服从对数正态分布, 实验结果与本文预测的概率疲劳寿命分布如图 9所示, 实验寿命均位于预测概率寿命分布的95%置信度双侧分位数区间内, 从疲劳寿命可靠性角度验证了本文方法的有效性。
 |
图 8 搭接壁板破坏位置 |
搭接壁板实验疲劳寿命 周次
 |
图 9 搭接壁板预测疲劳寿命概率分布 |
3 结论
1) 本文建立了金属材料双尺度桥联方程, 将Lemaitre疲劳损伤演化模型概率化, 通过反演优化获取模型参数样本, 进而统计其概率特性。结合双尺度桥联方程和疲劳损伤演化概率模型, 对模型参数进行随机抽样, 通过损伤累积计算即可获得寿命样本, 统计获得寿命概率特性。
2) 本文对疲劳损伤演化模型进行了简化处理, 如忽略损伤和弹塑性本构方程的耦合、材料变形进入塑性阶段即发生损伤和材料随动强化等。对于晶体结构不同的金属材料, 其弹塑性本构方程和强化模型构建地越精确, 对疲劳损伤演化机理的表征和寿命预测也会越精确, 但相应的计算量也会大大增加, 因此本文对其进行了一定的简化, 而由此造成的偏差可通过材料实验数据反演获取的模型参数S和s得到一定的补偿, 故本文方法具有一定的合理性和普适性。
3) 完成了铝合金2024-T3光滑圆棒在6组应力水平下的疲劳实验, 基于实验数据获得了模型参数概率特性; 对某飞机搭接壁板进行了整体-细节有限元分析, 计算危险点应力应变。利用本文双尺度疲劳损伤演化模型对搭接壁板在常幅谱下的概率疲劳寿命进行预测。完成了相应的疲劳实验, 实验疲劳破坏位置与本文有限元分析预测的危险点位置一致, 实验寿命均落在模型预测寿命概率分布的95%置信度双侧分位数区间内, 验证了本文模型预测金属构件概率疲劳寿命的有效性。
References
- ASCE Committee on Fatigue and Fracture Reliability. Fatigue reliability[J]. ASCE Journal of the Structural Division, 1982, 108(1): 3–88 [Article] [Google Scholar]
- BaiEnjun, HuangShutao, XieLiyang. P-S-N curves fitting of small sample with fatigue lives obeying Weibull distribution[J]. Journal of Xi'an Jiaotong University, 2019, 53(9): 96–101 [Article] (in Chinese) [Google Scholar]
- LiuHongbin, ChenWei, LiuLin. Prediction method and verification of fatigue life for a turbine disk with bolt hole[J]. Journal of Northwestern Polytechnical University, 2019, 37(4): 744–750 [Article][Article] (in Chinese) [Google Scholar]
- LuoYuan, YanDonghuang, YuanMing. Fatigue reliability assessment of simply supported bridges subject to impact of stochastic vehicle loads[J]. Chinese Journal of Computational Mechanics, 2018, 35(4): 417–423 [Article] (in Chinese) [Google Scholar]
- MaYu'e, WangBo, XiongXiaofeng. Experimental study of fatigue damage of glass-fiber reinforced aluminum laminates(FMLs)[J]. Journal of Northwestern Polytechnical University, 2016, 34(2): 41–45 [Article] (in Chinese) [Google Scholar]
- DoudardC, CallochS, CugyP, et al. A probabilistic two-scale model for high-cycle fatigue life predictionsFatigue & Fracture of Engineering Materials & Structures, 2005, 28(3): 279–288 [Article] [Google Scholar]
- SantecchiaE, HamoudaA M S, MusharavatiF, et al. A review on fatigue life prediction methods for metals[J]. Advances in Materials Science and Engineering, 2016, 20161–26 [Article] [Google Scholar]
- TodinovM T. Necessary and sufficient condition for additivity in the sense of Palmgren-Miner rule[J]. Comput Mater Sci, 2001, 21101–110 [Article] [Google Scholar]
- KrajcinovicD, LemaitreJ. Continuum damage mechanics: theory and applications New YorkSpringer-Verlag1987 [Google Scholar]
- LemaitreJ, SermageJ P, DesmoratR. A two scale damage concept applied to fatigue[J]. International Journal of Fracture, 1999, 9767–81 [Article] [Google Scholar]
- EshelbyJ D. The determination of the elastic field of an ellipsoidal inclusion and related problems[J]. Proc Roy Soc London, 1957, A241376–196 [Article] [Google Scholar]
- LemaitreJ, DesmoratR, SauzayM. Anisotropic damage law of evolution[J]. European Journal of Mechanics, 2000, 19187–208 [Article] [Google Scholar]
- StephensM A. EDF statistics for goodness of fit and some comparisons[J]. Journal of the American Statistical Association, 1974, 69(347): 730–737 [Google Scholar]
All Tables
All Figures
|
图 1 Eshelby-Kroner局域化准则 |
| In the text | |
|
图 2 宏细观双尺度桥联模型隐格式求解算法流程框图 |
| In the text | |
|
图 3 铝合金光滑圆棒疲劳实验件 |
| In the text | |
|
图 4 蒙皮-带板搭接壁板 |
| In the text | |
|
图 5 蒙皮-带板整体有限元计算结果 |
| In the text | |
|
图 6 蒙皮-带板细节模型计算结果 |
| In the text | |
|
图 7 搭接壁板危险点细观应力应变滞回环 |
| In the text | |
|
图 8 搭接壁板破坏位置 |
| In the text | |
|
图 9 搭接壁板预测疲劳寿命概率分布 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.