EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 39 / No 2 (April 2021) JNWPU, 39 2 (2021) 341-349 Full HTML
Open Access
Issue
JNWPU
Volume 39, Number 2, April 2021
Page(s) 341 - 349
DOI https://doi.org/10.1051/jnwpu/20213920341
Published online 09 June 2021

© 2021 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

与平行轴和行星齿轮传动相比，多分支齿轮传动采用功率分流方式，能够实现大功率、大减速比、大扭矩传动，广泛应用于航空和舰船等动力系统中。

近年来出现的同轴功率分支因体积小、尺寸紧凑等优点越来越广泛地得到应用和重视[1-3]。White[4]在1989年就研究直齿圆柱齿轮功率分流传动系统的结构特点，提出相比于传统的行星齿轮传动具有可靠性强、承载能力大、结构紧凑、重量和噪声小等特点。Jose等[5]对分扭变速箱中圆柱齿轮传动在航空、舰船等领域的应用进行了全面研究，提出多个齿轮传动同时啮合的结构构型，并建立同步啮合数学模型，通过数值计算获得了各齿轮齿数选定方案。杨振等[6-7]在功率分流齿轮系统的动力学特性、传动平稳性及强度方面进行了相应的研究。相涯等[8]针对功率四分支齿轮传动系统在考虑各支路均载基础上建立了系统的配齿条件并进行了计算。李枝军等[9]针对圆柱齿轮分扭传动考虑配齿结果对系统动力学特性的影响而进行配齿条件研究，提出不同的配齿方法并进行计算分析。阎昌琪等[10]对功率双分支传动两级齿轮减速器优化设计进行了分析，建立了结构参数优化模型，并开发了相应的计算程序。综上所述，现有文献并没有涉及到对齿轮分支传动系统在每个支路同步啮合性能方面的研究。由于分扭传动齿轮结构是通过多个支路同时进行动力和运动传递，每个支路之间的运动互相影响，这为构型与配齿参数设计带来了困难。

本文针对同轴六分支分扭人字齿轮传动系统，根据其构型的特点及其配齿对系统性能的影响，考虑啮合相位和齿轮模数等几何参数，进行了齿轮配齿条件与配齿方法的理论研究，建立了分支齿轮传动传动比条件、邻接条件、同心条件和同步正确啮合条件的数学关系式，并对每个支路同步啮合进行研究，提出了同轴六分支齿轮传动系统的配齿设计方法，为输入与输出轴为同轴多分支传动齿轮系统构型设计提供了理论基础。

1 同轴六分支分扭人字齿轮传动系统的配齿条件

1.1 六分支分扭人字齿轮传动系统

为了满足大功率传动需要，齿轮分扭传动系统中一般多采用人字齿轮，本文以同轴六分支分扭人字齿轮传动系统为研究对象，如图 1所示。

该系统中第Ⅰ级传动为三分支, 即输入齿轮1同时驱动齿轮2i(i=1, 2, 3), 实现功率三分流; 第Ⅱ级传动为齿轮2i(i=1, 2, 3)与对应的齿轮3i(i=1, 2, 3)啮合, 各分支功率传递到双联齿轮3i-4i (i=1, 2, 3)上; 第Ⅲ级传动为齿轮41驱动齿轮5i(i=1, 2), 齿轮42驱动齿轮5i(i=3, 4), 齿轮43驱动齿轮5i(i=5, 6), 再次实现三重功率两分流; 第Ⅳ级传动中齿轮5i(i=1, 2, 3, 4, 5, 6)同时与输出轴上齿轮6啮合, 实现功率的汇流, 且输入轴与输出轴在同一条直线上, 完成功率输出。在确定该系统各轮齿数、位置角等几何参数时, 还要满足传动比、邻接和同心条件, 同时要考虑其运动性能相关的同步啮合条件。

thumbnail 图 1

同轴六分支分扭人字齿轮传动系统

1.2 传动比条件

设输入齿轮1的齿数z1, 齿轮2i(i=1, 2, 3)的齿数z2, 齿轮3i(i=1, 2, 3)的齿数z3, 齿轮4i(i=1, 2, 3)的齿数z4, 齿轮5i(i=1, 2, 3, 4, 5, 6)的齿数z5, 齿轮6的齿数z6, 则系统的总传动比为

式中: 第Ⅰ级传动比为i1=z2/z1; 第Ⅱ级传动比为i2=z3/z2; 第Ⅲ级传动比为i3=z5/z4; 第Ⅳ级传动比为i4=z6/z5。

设齿轮系统给定传动比为id=n1/n6, n1为输入转速, n2为输出转速。考虑系统受齿轮齿数为整数等影响, 实际传动比i与给定传动比id存在相对误差Δi。其许用值[Δi]一般取3%至5%之间[11], 即传动比条件为

1.3 邻接条件

图 2表示齿轮系统一个分支, 在同轴六分支分扭人字齿轮传动系统进行设计时, 要使各齿轮之间不发生相互碰撞, 必须保证齿轮1、31和齿轮51、52之间的齿顶圆必须有一定间隙。设该分支中齿轮1与齿轮21、31位置角为αg, 在αg取最大和最小值时齿轮几何极限分布如图 2所示。dia和di(i=1, 21, 31)分别表示齿轮1、21、31的齿顶圆和分度圆直径。由图 2可得齿轮1与齿轮31满足的条件为

式中, Oi(i=1, 2, 3)表示齿轮的几何中心。与齿轮1相啮合另2个分支也是此规律, 这里不再赘述。

设分支齿轮41、51、52和齿轮51、41、6之间位置角分别为θi(i=1, 2), 则当θ1取最大和最小值时齿轮几何极限分布如图 3所示。Oi(i=41, 51, 52, 6)表示齿轮41、51、52, 6几何中心。图 3中, dia和di(i=41, 51, 6)分别表示齿轮41、51、6的齿顶圆直径和分度圆直径。由图 3得齿轮51与齿轮52邻接条件

齿轮41和齿轮6邻接条件为

式中, , 齿轮1、31和齿轮41、6具有相同的中心距。与齿轮4相啮合其他2个分支也是此规律, 这里不再赘述。

thumbnail 图 2

系统第Ⅰ级单一分支极限位置
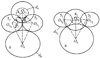thumbnail 图 3

系统第Ⅲ级单一分支极限位置

1.4 同心条件

该同轴六分支人字齿轮分扭传动系统同心表现为: 3个双联齿轮上的齿轮3i(i=1, 2, 3)和齿轮4i(i=1, 2, 3)轴线与双联齿轮轴线重合, 且平行于齿轮5i(i=1, 2, 3, 4, 5, 6)旋转轴线。如图 4设θi(i=1, 3)分别表示齿轮41、51、52和齿轮6、51、52之间的位置角。di(i=41, 51, 6) 表示齿轮41、51、6的分度圆直径, Oi(i=41, 51, 52, 6)表示齿轮41、51、52、和齿轮6几何中心。由图 4可得该分支满足

将其各齿轮分度圆直径代入(6)式, 可得

同理其他2个双联齿轮啮合齿轮分支同心条件也是此规律, 这里不再赘述。

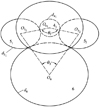thumbnail 图 4

齿轮系统分支同心简图

1.5 同步啮合条件

该齿轮系统存在3个双联齿轮, 为了使得到构型满足互换性使用要求, 在一般情况下, 2个双联齿轮不完全一样, 但仍假设双联齿轮位置角完全相同[12]。如图 5所示, 规定点Q齿和点P齿处在同一平面ABCD内, 位置角为0°进行分析。

图 6表示同轴六分支分扭人字齿轮传动系统轴向构型简图, 各齿轮分度圆相切处代表该处相啮合。齿轮传递载荷受齿轮副综合刚度K影响很大[13], 为了满足齿轮系统传动时均布安装和运动同步, 规定齿轮1和齿轮2i(i=1, 2, 3)之间位置角为120°; 以齿轮1为中心, 双联齿轮上的齿轮3i(i=1, 2, 3)和齿轮4i(i=1, 2, 3)分别与齿轮1位置角为120°。因此确定齿轮系统同步啮合问题, 只要保证齿轮41、5i(i=1, 2)与齿轮6, 齿轮42、5i(i=3, 4)与齿轮6, 齿轮43、5i(i=5, 6)与齿轮6分别同步啮合。

由以上分析可知, 只要保证与齿轮1相啮合的三分支其中一个分支, 便能使轮系满足同步正确啮合。图 7表示以齿轮41、5i(i=1, 2)与齿轮六分支为对象分析, 假设齿轮31和41构成位置角为0°双联齿轮。点A, B, C和D分别表示齿轮41、51、52和输出齿轮6的圆心。角θi(i=1, 2, 3, 4)为各相邻齿轮连心线组成四边形的4个内角, 即齿轮的位置角。假设齿轮1、21和31调整到正确啮合, 若要保证构型同步啮合, 只要齿轮41、51、52和齿轮6正确啮合即可。

规定双联齿轮初始状态: 左边齿Q和齿P通过齿轮连心线AB; 右边齿q和齿p需按图 7表示的运动方向转动ψ+Δψ角才通过连心线AD, ψ表示齿轮52上n个齿距的圆心角, Δψ表示齿轮52上n*个齿距的圆心角(n取整数, 0 < n* < 1)。在齿轮41上θ1=ϕ+Δϕ, ϕ表示s个齿距的圆心角, Δϕ表示s*个齿距的圆心角(s取整数, 0 < s* < 1)。

定义Ti(i=0, 1, 2)时刻说明分支的啮合条件, 分析如下:

T0时刻: 将T0定义为图 7所示的齿轮初始啮合状态时刻, 齿轮1、21和齿轮31正确啮合, 齿轮51的齿E通过连心线BC, 齿轮52的齿G再顺时针转动ψ+Δψ通过连心线AD。

T1时刻: 将T1定义为随齿轮转动, 齿轮51的Q点与齿轮6的F点相切时刻。此刻, Q点与F点相切, 而点G与H未相切, 但齿轮51、52和齿轮6转过相同齿距数, 对应如图 7所示的粗实线标记弧长。

T2时刻: 将T2定义为随齿轮继续转动, 齿轮52的G点与齿轮6的H点相切时刻。此刻, G点和H点相切, 而Q点与F点退出相切。从T0到T2时刻, 齿轮51、52和齿轮6同样转过相同齿距数, 对应如图 7所示的灰色实线标记弧长。

由此可知, T1时刻相切唯一对应此处轮齿啮合位置, T2时刻相切唯一对应此处轮齿啮合位置。要保证齿轮41、51、52和齿轮6正确啮合, 只要T1和T2时刻齿轮6上的F和H点啮合的轮齿具有相同啮合位置, 即齿轮6上的F和H点之间的弧长对应的齿距数为整数, 称齿轮同步啮合的啮合条件。如果不能满足此啮合条件, 则该同轴六分支分扭人字齿轮传动系统至少存在一处啮合位置干涉。

设齿轮41、51、52和齿轮6的齿数分别为: z41、z51、z52和z6, 根据上述啮合条件和各齿轮的齿数, 齿轮51圆心角θ2内的齿距数为

齿轮6圆心角θ3内的齿距数为

齿轮52上灰色标记的弧线对应的圆心角齿距数为

式中, 。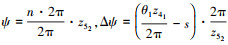

根据啮合条件, 齿轮6上的F和H点之间弧长齿距数为整数, 可得到齿轮齿数与位置角的关系

式中, N为整数, 将(8)~(10)式代入(11)式, 经整理得

式中, (N+s-z51-n)表示一个整数, 以整数M代之, 可得齿轮啮合条件简化后的表达式

在四边形ABCD中, 由内角和定理得

在四边形ABCD中, 由对角线余弦定理得

标准斜齿圆柱齿轮分度圆半径表示为

式中, ri, zi, mit, min和β分别表示齿轮i的分度圆半径、齿数、端面模数、法面模数和螺旋角, i=41, 51, 52, 6。代入(15)式、(16)式得简化后为

式中, mL=m41t=m51t=m52t, mR=m41t=m6t=m52t

式中: mL=m41t=m51t=m6t, mR=m41t=m6t=m52t

根据齿轮啮合条件, 相啮合齿轮模数相等, 可得

若已知齿轮齿数zi和模数mit, 则可通过(13)、(14)、(17)、(20)和(21)式组成的方程组求未知位置角θ1, θ2, θ3和θ4, 且方程组的解受(13)式中的整数M取值影响。

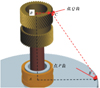thumbnail 图 5

双联齿轮位置角
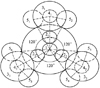thumbnail 图 6

同轴六分支分扭人字齿轮传动系统轴向构型简图
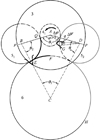thumbnail 图 7

分支啮合条件简图

2 配齿计算方法

针对图 6所示的同轴六分支分扭人字齿轮传动系统, 由于齿轮2i(i=1, 2, 3)、齿轮3i(i=1, 2, 3)、齿轮4i(i=1, 2, 3)和齿轮5i(i=1, 2, 3, 4, 5, 6)均匀分布于输入齿轮1轴线和输出齿轮6轴线同一直线周围, 只要确定齿轮1、21、31、41、5i(i=1, 2)与齿轮6的位置, 整个传动系统中齿轮之间位置便确定。针对图 7分支齿轮传动, 配齿条件计算的步骤如下:

1) 由初步设计方法得到满足齿轮传动强度和传动比等参数的初步齿数(齿轮1、21、31、41、5i(i=1, 2)与齿轮6的齿数分别为Z1、Z2、Z3、Z4、Z5、Z6), 通过进行齿数组合调整, 满足上述配齿条件。

2) 调整齿轮41、5i(i=1, 2)、6的齿数组合。在齿轮传动系统中, 相互啮合的齿轮越多, 就会构成封闭啮合链, 需要满足的配齿条件就越多, 因此首先要调整齿轮41、5i(i=1, 2)、6的齿数, 使之满足相邻条件和同心条件后再调整齿轮1、21、31的齿数。

3) 确定布置角θ1、θ2、θ3、θ4。人字齿轮[15]亦称为“双斜齿轮”, 根据圆柱斜齿轮啮合条件, 可知此分支齿轮41、5i(i=1, 2)、6的法向模数相等, 记m41n=m51n=m52n=m6n。由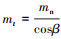(β表示齿轮螺旋角)可知端面模数相等, 记m41t=m51t=m52t=m6t。齿轮51和52对称分布于齿轮41, 可知θ2=θ4。将初步参数代入(13)式得

式中, M=(N+s-Z51-n), 由θ2=θ4可知存在3个未知变量, 故在四边形ABCD中只需要用一次对角线余弦定理

对(22)、(23)和(24)式组成的方程组进行求解, 会得到一个关于θ1的超越方程

只要求出θ1的值, 则可得θ3和θ2

图 8表示超越方程(25)在M取为0的f(θ1)求解曲线。当整数M取不同值时，求解曲线形状不变, 只是求解曲线的位置在f(θ1)方向上下移动。图 8上的K点表示曲线与横轴的交点, 即当f(θ1)=0未知量θ1值。在θ1∈[0, 2π]范围内, 求解曲线存在一个峰谷, 当整数M取某值时, 超越方程的求解曲线与x(θ1)有2个交点, 即存在2个θ1值。在单一分支中, 已知齿轮齿数、模数, 可得方程(25)~(27)式解, 即齿轮之间的位置角。然后检验齿轮51与齿轮52邻接条件式(4)和齿轮41和齿轮6邻接条件(5)式及分支的同心条件(7)式是否同时满足, 若满足则进行下一步计算, 若不满足则调整整数M继续调整齿轮41、齿轮5i(i=1, 2)和齿轮6的齿数。

4) 确定齿轮1、21、31的布置角θ5、θ6、θ7。由于齿轮1与齿轮6是同轴的, 而齿轮2i(i=1, 2, 3)以齿轮1圆心为中心均匀分布。由图 9可知

Oi(i=1, 2, 3)表示齿轮1、21、31的几何中心, di(i=1, 2, 3)表示齿轮1、21、31分度圆直径。

如图 9所示, 初始参数确定的齿轮分度圆半径满足关系式: DO2O3+DO1O2>DO1O3, 就能确定布置角θ5、θ6、θ7。然后检验齿轮1、21、31的邻接条件式(3)是否满足, 最后检验是否满足传动比式(1)和(2)。若满足说明各齿轮齿数满足配齿条件, 若不满足则继续调整齿轮1、21、31的齿数, 甚至重新选定整数M调整齿轮41、5i(i=1, 2)、6的齿数。图 10表示配齿计算过程流程图。

thumbnail 图 8

超越方程(25)在M=0的求解曲线
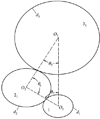thumbnail 图 9

齿轮1、21、31分支简图
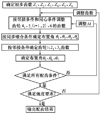thumbnail 图 10

配齿方法流程图

3 配齿算例

某舰船的动力传动系统采用同轴六分支分扭人字齿轮传动。其初步设计参数如表 1所示, 从表 1得齿轮41、5i(i=1, 2)、6同步啮合条件均不满足。

采用上述同步啮合配齿方法, 在整数M取不同值时, 方程式(25)~(27)得不同解。表 2给出了整数M取-168到45之间不同值时的位置角。当M=-168, 齿轮41处于上极限位置, 随着整数M取值变化, 在M=45时, 齿轮41处于下极限位置。

图 11表示分支的2个极限位置, 黑色粗曲线表示齿轮重合。

图 12所示为M=-75时, θ1=55.25°、θ2=139.40°、θ3=25.95°、θ4=139.40°, 考虑实际制造和安装误差等因素影响, 齿轮51和齿轮52很容易发生干涉。图 13所示为M=30时, θ1=204.75°、θ2=46.04°、θ3=63.17°、θ4=46.04°, 再考虑实际制造和安装误差等因素影响, 齿轮41和齿轮6很容易发生干涉。图 14为M=16时, θ1=180°、θ2=63.90°、θ3=52.20°、θ4=63.90°, 分支各齿轮不发生干涉。

表 3为M=16时的配齿结果, 此时布置角θ1=180°、θ2=63.90°、θ3=52.20°、θ4=63.90°, 该结果不仅满足同步啮合条件, 也满足传动比条件、邻接条件和同心条件。图 15表示表 3数据参数化设计得到同轴六分支分扭人字齿轮传动系统的三维结构模型, 各支路满足均布条件和同步啮合条件。如图 16所示, 通过三维软件proe验证分支各齿轮之间的啮合状态, 无干涉且具有良好的接触状态。因此该配齿方法在同轴的多分支分扭齿轮传动系统的构型设计上具有普适性, 所得结论同样适用于较为简单的二分支、三分支及含有惰轮三分支等传动系统设计。

表 1

齿轮初步参数

表 2

系统分支中齿轮之间布置角

thumbnail 图 11

2个极限位置
thumbnail 图 12

M=-75时分支啮合简图
thumbnail 图 13

M=30时分支啮合简图
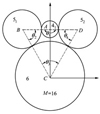thumbnail 图 14

M=16时分支啮合简图
表 3

齿轮设计参数

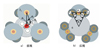thumbnail 图 15

同轴六分支人字齿轮传动系统
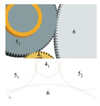thumbnail 图 16

齿轮41、51、52和6之间啮合状态

4 结论

1) 在设计同轴六分支分扭齿轮传动系统中除了满足传动比条件外, 还必须满足与装配有关的邻接和同心条件, 更重要的是满足与传动性能有关的同步啮合条件。

2) 同轴分扭齿轮传动系统同一平面上相互啮合的传动结构同步配齿条件与各个齿轮的模数、螺旋角无关, 只与各齿轮的齿数和位置角相关, 故本文方法也适用于由直齿轮和斜齿轮组成的分支传动。

3) 文中建立关于齿数、模数和位置角之间关系的超越方程, 在整数M取不同值时, 超越方程解的曲线形状不变, 只是解的曲线位置在f(θ1)方向上下移动, 能得到不同的齿轮传动构型。

References

  1. KahramanA. Load sharing characteristics of planetary transmissions[J]. Mechanisms and Machine Theory, 1994, 29(8): 1151–1165 [Article] [Google Scholar]
  2. Zhu C C, Xu X Y, Wang H J. Modal prediction and sensitivity analysis of wind-turbine planetary gear system with flexible planet pin[J]. Advanced Science Letters, 2011, 4(3): 1219–1224 [Article] [Google Scholar]
  3. Xu L J, Chen N. Nonlinear dynamic study and vibration reduction of a power turret gear train with modified design parameters[J]. Proceedings of the Institution of Mechanical Engineers, 2015, 229(10): 1745–1759 [Article] [Google Scholar]
  4. White G. Split torque helicopter transmissions with widely separated engines[J]. Journal of Aerospace Engineering, 1989, 20353–65 [Article] [Google Scholar]
  5. Jose A, Abraham R. Feasible geometrical configurations for split torque gearboxes with idler pinions[J]. Journal of Mechanical Design, 2010, 132(12): 1–8 [Article] [Google Scholar]
  6. Yang Zhen, Wang Sanmin, Fan Yesen. Nonlinear dynamicscharacteristics of split-torque gear transmission system[J]. Chinese Journal of Mechanical Engineering, 2008, 44(7): 52–57 [Article] (in Chinese) [Google Scholar]
  7. Wang Hui, Yuan Ru, Wang Sanmin. Optimal design on equal stress intensity of split-torque gear[J]. Mechanical Trans-mission, 2011, 36(3): 40–42 [Article] (in Chinese) [Google Scholar]
  8. Xiang Ya, Wang Sanmin, Yuan Ru. Research on tooth matching condition of the four-path torque-splitting gear transmission[J]. Mechanical Transmission, 2012, 36(5): 6–9 [Article] (in Chinese) [Google Scholar]
  9. Li Zhijun, Zhu Rupeng, Bao Heyun, et al. Tooth matching of split torque transmission[J]. Journal of Central South University, 2014, 45(2): 414–420 [Article] (in Chinese) [Google Scholar]
  10. Yan Changqi, Zheng Jing, Wang Jianjun. Optimal design for a power dual branch transmission two-grade gear reducer[J]. Journal of Harbin Engineering University, 2011, 32(7): 884–889 [Article] (in Chinese) [Google Scholar]
  11. Abraham Segade Robleda, et al. Split torque gearboxes: requirements, performance and applications[M]. Mechanical Engineering, 2012: 56–74 [Google Scholar]
  12. Feng G S, Xie Z F, Zhou M. Geometric design and analysis of face-gear drive with involute helical pinion[J]. Mechanism and Machine Theory, 2019, 134(2): 169–196 [Article] [Google Scholar]
  13. Kan Y Z, Sun D Y, Luo Y, et al. Optimal design of the gear ratio of a power reflux hydraulic transmission system based on data mining[J]. Mechanism and Machine Theory, 2019, 142103600 [Article] [Google Scholar]
  14. Wang C. High power density design for planetary gear transmission system[J]. Journal of Mechonical Engineering Science, 2019, 233(16): 5647–5658 [Article] [Google Scholar]
  15. Zhu L Y, Shi J F, Guo X F. Modeling and dynamics analyzing of a torsional-bending-pendular face-gear drive system considering multi-state engagements[J]. Mechanism and Machine Theory, 2020, 149: 103790[Article] [Google Scholar]

All Tables

表 1

齿轮初步参数

In the text
表 2

系统分支中齿轮之间布置角

In the text
表 3

齿轮设计参数

In the text

All Figures

thumbnail 图 1

同轴六分支分扭人字齿轮传动系统
In the text
thumbnail 图 2

系统第Ⅰ级单一分支极限位置
In the text
thumbnail 图 3

系统第Ⅲ级单一分支极限位置
In the text
thumbnail 图 4

齿轮系统分支同心简图
In the text
thumbnail 图 5

双联齿轮位置角
In the text
thumbnail 图 6

同轴六分支分扭人字齿轮传动系统轴向构型简图
In the text
thumbnail 图 7

分支啮合条件简图
In the text
thumbnail 图 8

超越方程(25)在M=0的求解曲线
In the text
thumbnail 图 9

齿轮1、21、31分支简图
In the text
thumbnail 图 10

配齿方法流程图
In the text
thumbnail 图 11

2个极限位置
In the text
thumbnail 图 12

M=-75时分支啮合简图
In the text
thumbnail 图 13

M=30时分支啮合简图
In the text
thumbnail 图 14

M=16时分支啮合简图
In the text
thumbnail 图 15

同轴六分支人字齿轮传动系统
In the text
thumbnail 图 16

齿轮41、51、52和6之间啮合状态
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.