| Issue |
JNWPU
Volume 39, Number 2, April 2021
|
|
|---|---|---|
| Page(s) | 439 - 447 | |
| DOI | https://doi.org/10.1051/jnwpu/20213920439 | |
| Published online | 09 June 2021 | |
Competitive failure analysis of a stochastic degradation system based on performance characteristics fusion
基于性能指标融合的随机退化系统竞争失效分析
1
College of Mathematics and Computer Science, Yan'an University, Yan'an 716000, China
2
School of Mechanical Engineering, Northwestern Polytechnical University, Xi'an 710072, China
Received:
2
September
2020
With the aim of solving the reliability modeling and calculation of multivariate stochastic degradation systems, two stochastic degradation models based on the bivariate Wiener process are proposed, in which two performance characteristics are composited to one variable. Two different failure modes including the defect-based failure and the duration-based failure are considered. The explicit expressions of the system reliability are derived in the cases that the performance characteristics are not composited or the performance characteristics are composited according to the linear combination of the degradation measurements. An algorithm based on the Monte Carlo simulation is proposed to simulate the degradation process, in which the performance characteristics are composited in arbitrary forms, and the correctness of the analytical results is also verified. Finally, some numerical examples are presented to illustrate the present reliability assessment method。
摘要
针对多元随机退化系统可靠性建模与计算的难点,考虑性能指标融合,构建了2个基于二元Wiener过程的随机退化模型;考虑退化失效和持续时间失效2类竞争失效形式,推导了性能指标不进行融合以及性能指标按照退化量的线性组合进行融合情形下,持续时间失效阈值为常数和随机变量时的系统可靠度解析表达式;提出了基于蒙特卡洛模拟的数值模拟算法,验证了解析结果的正确性,并可用于模拟性能指标按照任意形式进行融合情形下二元以及多元随机退化系统的可靠度。最后,通过数值算例验证了所提出模型与计算方法的有效性。
Key words: degradation system / Wiener process / defect-based failure / duration-based failure / reliability
关键字 : 随机退化系统 / Wiener过程 / 退化失效 / 持续时间失效 / 可靠性
© 2021 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
关于随机退化系统的研究可以追溯到20世纪60年代,但是直到20世纪90年代才引起国内外学者的重视,近年来随着传感器技术和计算技术的发展,随机退化系统的可靠性建模与分析已经发展为可靠性理论与工程领域研究的热点之一[1-4]。目前,在多元随机退化系统的研究中,通常假设系统的退化程度由每个性能指标的退化量直接进行描述[5]; 除此之外,在实践中,还经常将性能指标融合成一个变量间接地描述系统的健康状态[6]。例如,船舶艉轴承是船舶动力装置的主要组成部分,艉轴承间隙是描述船舶艉轴承健康状态的重要指标,而艉轴承间隙可通过艉轴直径磨损量和艉轴承衬磨损量来确定,当艉轴直径磨损量和艉轴承衬磨损量之和(即将二者融合为一个新的变量)达到失效阈值(即允许的间隙最大值)时,船舶艉轴承失效[7]。杨圆鉴[7]采用Wiener过程描述艉轴直径磨损量和艉轴承衬磨损量的退化过程,对船舶艉轴承的可靠性进行了评估,但是为了计算方便,假设二者是相互独立的。实际上,由于受共同的工作环境及应力影响,艉轴直径磨损量和艉轴承衬磨损量的退化过程是相关的,并且系统性能指标退化过程的相关性在许多系统中广泛存在,因此在多元随机退化系统的可靠性建模与分析中考虑性能指标的相关性更加符合实际,但是多元性能指标之间的相关性却给退化建模带来了巨大的挑战[4, 8],其主要原因在于多元随机过程(例如多元Wiener过程)的首达时分布是目前学术界无法解决的难题[9]。作为多元随机退化系统的特殊情形,二元随机退化系统是最基本、最重要的情形,是研究多元随机退化系统的基础,不仅能够反映多元情形下的许多本质问题,而且相比多元情形在数学上更易于处理[10],因此本文以二元随机退化系统为主要研究对象。
在随机退化系统的可靠性建模中,除了建立描述系统退化过程的退化模型,还要确定系统失效的准则,两者缺一不可。学者们通常将系统的寿命定义为退化过程关于失效阈值的首达时间,一般称这种失效为退化失效[11-13]。事实上,许多系统的退化过程存在警戒阈值[14],在退化量达到警戒阈值前,系统处于正常状态,但是超过警戒阈值后,系统将处于缺陷状态,例如警戒水位、腐蚀裕量等[15-16],系统在2种状态下的退化速率通常是不同的。此时,如果采用相同参数的随机过程对系统两阶段退化过程进行描述,可能会导致可靠性指标计算的误差[17]。此外,上述系统除了发生因退化导致的退化失效外,系统还会发生突发失效[18-19],例如系统在缺陷状态的持续时间过长,系统也会失效。Dong和Cui[20]考虑退化失效和持续时间失效,构建了基于非平稳随机过程的两阶段退化模型,给出了系统可靠度等可靠性指标。Qiu和Cui[21]考虑不同失效准则,给出了最优维修策略。上述文献均以一元随机退化系统为研究对象,而在二元或多元随机退化系统的可靠性建模与分析中均只考虑退化失效[22-26],因此探讨二元或多元随机退化系统的竞争失效分析问题具有重要的现实意义。
基于上述分析,本文的主要研究内容包括:①针对二元随机退化系统,考虑性能指标的相关性、性能指标融合以及退化失效和持续时间失效2类竞争失效形式,构建基于二元Wiener过程的可靠性模型。②在性能指标不进行融合以及性能指标按照退化量的线性组合进行融合情形下,推导持续时间失效阈值为常数和随机变量时的系统可靠度解析表达式。③提出基于蒙特卡洛模拟的数值模拟算法, 模拟性能指标按照任意形式进行融合情形下二元以及多元随机退化系统的可靠度,并用于验证解析结果的正确性。
1 问题描述与可靠性建模
考虑二元随机退化系统,根据性能指标是否进行融合,构建2个可靠性模型。性能指标融合是指利用新变量描述性能指标之间的关系,即系统的退化程度由性能指标退化量的函数进行描述。假设X(t)=(X1(t), X2(t))′, Xi(t)为系统的第i个性能指标在时刻t的退化量(i=1, 2), 则在性能指标融合情形下, 系统在时刻t的退化程度由X(t)的函数H(x1, x2)进行描述, 其中x1和x2为X1(t)和X2(t)的样本实现值。
模型1 性能指标不进行融合情形下的可靠性模型。
1) 两阶段退化过程
假设系统的退化过程包括正常阶段(或第一阶段, 即从新系统投入运行到缺陷发生时刻)和缺陷阶段(或第二阶段, 即从缺陷发生时刻到失效发生时刻), 从而系统的状态包括正常、缺陷和失效。令
式中: Xik(t)是系统的第i个性能指标在第k个阶段时刻t的退化量, i=1, 2, k=1, 2;Γ1是变点, 定义为2个性能指标首达警戒阈值的时刻, 若定义随机变量γi=inf{t>0:Xi1(t)≥Di1}, i=1, 2, 则Γ1=min{γ1, γ2}。
2) 二元Wiener过程退化模型
由于受共同的环境应力, 2个性能指标的退化过程是相关的, 在每个阶段采用二元相关Wiener过程描述系统的退化程度, 即
式中: x0=(x110, x210)′是系统的初始退化量, 并假设x0=(0, 0)′, 即系统在时刻t=0是全新的; X(Γ1)=(X11(Γ1), X21(Γ1))′为系统在变点处的退化量向量。对于i=1, 2, k=1, 2, μk=(μ1k, μ2k)′为漂移系数向量; μik为系统第i个性能指标在第k个阶段的漂移系数; Σk是第k个阶段的扩散矩阵, 使得
为协方差矩阵, ρk是相关系数, 描述2个性能指标在第k个阶段的相关性, σ1k和σ2k为标准差; W(t)=(W1(t), W2(t))′, {W1(t), t≥0}和{W2(t), t≥0}是相互独立的标准Wiener过程。具体的, 如果记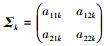 , 则
, 则
显然, 如果ρ1=ρ2=0, 则2个性能指标的退化过程是相互独立的。为了方便, 记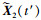 =X(Γ1)+μ2t′+Σ2W(t′), 其中
=X(Γ1)+μ2t′+Σ2W(t′), 其中 ,
, 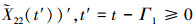 。
。
3) 竞争失效
当一个性能指标的退化量超过其退化失效阈值时, 或系统在缺陷阶段的持续时间超过持续时间失效阈值τ时, 系统失效。系统的退化路径如图 1所示, 其中γ和y分别为Γ1和Y的实现值。
 |
图 1 模型1下系统的退化路径 |
因此, 模型1下系统的寿命为
式中, Λ1=min{λ1, λ2}, λi=inf{t≥0, 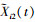 ≥Di2}, Di2(i=1, 2)为性能指标的退化失效阈值。
≥Di2}, Di2(i=1, 2)为性能指标的退化失效阈值。
模型2 性能指标融合情形下的可靠性模型。
本文考虑H(x1, x2)的3种表达形式:
① H(x1, x2)=k1x1(t)+k2x2(t), k1, k2∈R; ②H(x1, x2)=|x1(t)-x2(t)|; ③一般形式。
与模型1的不同之处在于变点以及系统寿命的表达形式。在模型2下, 变点定义为2个性能指标退化量的函数关于警戒阈值L1的首达时刻, 即
则系统的寿命为
式中,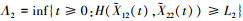 。
。
2 系统可靠度
本节将给出系统可靠度的解析表达式, 包括模型1和模型2下H(x1, x2)=k时2种情形, 以及模型2下H(x1, x2)为一般函数时可靠度的模拟算法。
1) 模型1下系统可靠度
根据失效准则, 系统的可靠度为
首先, 假设持续时间失效阈值为常数。
注意到Γ1=min{γ1, γ2}以及γi=inf{t≥0:Xi(t)≥Di1}, i=1, 2, 通过对一个性能指标达到失效阈值的时刻及另一个未达到失效阈值的性能指标在该时刻的数值取条件, 得到
式中:x01=(D11, x2)′, x02=(x1, D21)′; 对于i, j=1, 2, i≠j, fo(Xj1, γi)(xj, ti)的表达式由文献[27]的公式(21)给出;  。
。
当其中的一个性能指标达到失效阈值时, 系统将进入缺陷阶段。根据Xi2(t)(i=1, 2)的定义, 当γ1≤γ2时, 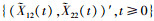 是以(D11, x2)为起点的二元Wiener过程; 当γ2≤γ1时,
是以(D11, x2)为起点的二元Wiener过程; 当γ2≤γ1时, 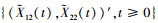 是以(x1, D21)为起点的二元Wiener过程。因此
是以(x1, D21)为起点的二元Wiener过程。因此
式中, f(λ1, λ2)(u1, u2|x0i)的表达式由文献[27]的公式(2)给出。将(8)式代入(7)式, 得到
在工程实践中, 持续时间失效阈值通常是随机变量。下面假设持续时间失效阈值是具有概率密度函数fτ(t)和分布函数Fτ(t)的随机变量, 并考虑以下2种情形:一种情形是分布在[0, +∞)上的随机变量; 一种情形是分布在[τ1, τ2]上的随机变量, 其中τ1和τ2是正常数。
如果持续时间失效阈值τ是分布在[0, +∞)上的随机变量, 例如τ是服从指数分布或韦布尔分布的随机变量, 则(9)式变为
类似的, 可以得到持续时间失效阈值τ是分布在[τ1, τ2]上的随机变量时的可靠度。
2) 模型2下H(x1, x2)=k时系统可靠度
根据Γ2的定义, 如果τ是常数, 系统可靠度为
式中: f(X1, Γ2)(x1, u)是X1(Γ2)和Γ2的联合概率密度函数, 满足
又由于(X11(u), X21(u))是服从二元正态分布BVN(uμ1, uΣ′1Σ1)的随机变量, 从而X11(u)是服从正态分布N(uμ11, uσ112)的一元随机变量, 因此
从而, 要得到(11)式的解析表达式, 只需得到变点Γ2的概率密度函数fΓ2(u)即可。然而, 除了H(x1, x2)的一些特殊形式外, fΓ2(u)的解析表达式是很难获得的。
下面, 给出H(x1, x2)=k1x1+k2x2情形下的系统可靠度。由(2)式知
式中,{B1(t)=[(k1a111+k2a211)W1(t)+(k1a121+k2a221)W2(t)]/δ1, t≥0}是标准Wiener过程, 。
。
由Γ2的定义, 即Γ2=inf{t>0:H(X11(t), X21(t))≥L1}, fΓ2(u)为{Z1(t), t≥0}关于L1的首达时的概率密度函数, 其中Z1(t)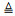 (k1μ11+k2μ21)t+δ1B1(t)。因此, 由(13)式可以得到
(k1μ11+k2μ21)t+δ1B1(t)。因此, 由(13)式可以得到
将(12)式和(14)式代入(11)式, 得到
接下来, 给出FΛ2(t-u|x1, x2)的解析表达式。注意到k1x1+k2x2=L1, 与(13)式类似
式中,{B2(t)=[(k1a112+k2a212)W1(t)+(k1a122+k2a222)W2(t)]/δ2, t≥0}是标准Wiener过程, δ2= 。
。
由Λ2的定义, 即Λ2=inf{t≥0:H(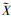 21(t),
21(t), 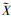 22(t))≥L2}, FΛ2(v|x1, x2)为{Z2(t), t≥0}关于L2的首达时的分布函数, 其中Z2(t)=L1+(k1μ12+k2μ22)t+δ2B2(t)。因此
22(t))≥L2}, FΛ2(v|x1, x2)为{Z2(t), t≥0}关于L2的首达时的分布函数, 其中Z2(t)=L1+(k1μ12+k2μ22)t+δ2B2(t)。因此
将(15)式和(16)式代入(10)式, 得到H(x1, x2)=k1x1+k2x2情形下的系统可靠度
注:①如果令τ=0, (17)式将变为单阶段一元随机退化系统的可靠度[11]; ②如果令τ→+∞, (17)式将变为两阶段一元随机退化系统的可靠度[11]; ③如果τ是随机变量, 通过积分可以得到相应的系统可靠度的解析表达式。
3) 模型2下H(x1, x2)为一般函数时系统可靠度的数值模拟
由(11)式可以发现, 性能指标按照任意形式进行融合情形下的系统可靠度表达式在形式上是简单的, 但是对一般H(x1, x2)而言, Λ2和Γ2的分布函数的表达式并不容易求解。基于蒙特卡洛模拟的算法来模拟系统可靠度, 具体的模拟算法流程如算法1所示。
算法1 模型2下H(x1, x2)为一般函数时系统可靠度的模拟算法
步骤1 设定参数值, 包括初始时刻t=0, 初始退化量x0, 漂移参数向量μ1和μ2, 扩散矩阵Σ1和Σ2, 警戒阈值L1, 退化失效阈值L2, 持续时间失效阈值τ和其他相关参数。令模拟次数和步长分别为N和Δt。
步骤2 对于i=1, 2, …, N, 执行步骤3至4。
步骤3 生成期望为0, 协方差矩阵为ΔtΣ1Σ′1的二元正态分布随机数, 然后计算X1(t)=(X11(t), X21(t))′。如果H(X11(t), X21(t))≥L1, 得到变点的数据Γ2、2个性能指标在Γ2时刻的退化量X11(Γ2)和X21(Γ2), t←t+Δt, 然后转到步骤4;如果H(X11(t), X21(t)) < L1, t←t+Δt, 然后转到步骤3。
步骤4 如果t≥Γ2+τ, 得到一个失效时间数据Γ2+τ, 并将其存入数组A, 然后转到步骤5;如果t<Γ2+τ, 生成期望为0, 协方差矩阵为ΔtΣ2Σ′2的二元正态分布随机数, 然后计算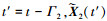 =
=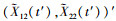 ; 如果
; 如果 , 得到一个基于持续时间失效的失效时间数据Γ2+t′, 并将其存入数组A, 然后转到步骤5;如果
, 得到一个基于持续时间失效的失效时间数据Γ2+t′, 并将其存入数组A, 然后转到步骤5;如果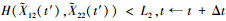 , 然后转到步骤4。
, 然后转到步骤4。
步骤5 完成模拟, 根据失效数据集A计算系统可靠度。
注:1) 如果持续时间失效阈值是随机变量, 只需在步骤4中增加在指定的分布中生成独立同分布的随机数即可。
2) 算法1还适用于基于性能指标融合的多元随机退化系统的可靠度计算, 即随机退化系统具有多个性能指标(例如n个性能指标)时, 只需做如下修改: ①在步骤3和步骤4中生成多元正态分布随机数, 即扩散矩阵Σ1和Σ2分别为n×n阶矩阵; ②采用H(x1, x2, …, xn)描述性能指标融合, 即将各性能指标退化量的数值代入H(x1, x2, …, xn)描述系统的退化程度。
3 数值算例
本节给出一些数值算例来验证所构建模型的有效性, 并对模型中的参数进行灵敏度分析, 探讨模型参数对随机退化系统可靠性指标的影响。
假设2个性能指标退化量的警戒阈值和退化失效阈值分别为0.2和0.4, 持续时间失效阈值τ=4。在第一阶段, μ11=μ21=0.016 7, σ11=σ21=0.045 0, ρ1=-0.786 2;在第二阶段, μ12=μ22=0.024 0, σ12=σ22=0.060 4, ρ2=-0.694 3, 从而两阶段的协方差矩阵分别为
1) 模型1下系统可靠度
为了验证解析解的正确性, 利用(9)式给出基于解析解的可靠度曲线, 利用算法1给出基于模拟解的可靠度曲线, 并将2种情形下的可靠度曲线画在同一个图中, 如图 2所示。此外, 解析结果和数值模拟结果的平均误差可以通过 进行估计, 其中n为数据点的个数, xi和yi分别为解析解和数值模拟解的数值。图 2中二者的平均误差为0.006 7, 可以发现, 解析解与模拟解吻合良好。
进行估计, 其中n为数据点的个数, xi和yi分别为解析解和数值模拟解的数值。图 2中二者的平均误差为0.006 7, 可以发现, 解析解与模拟解吻合良好。
 |
图 2 模型1下基于模拟解和解析解的系统度曲线 |
为了得到持续时间失效阈值对系统可靠性的影响, 下面给出持续时间失效阈值为具有不同均值的随机变量情形下的系统可靠度曲线。假设持续时间失效阈值服从分布在[0, 8]上的β分布, 且取不同的参数a和b, 即: a=1且b=1、a=1且b=2、a=1且b=10、a=2且b=1、a=10且b=1。相应的, 持续时间失效阈值的均值分别为 。根据(10)式, 得到相应的系统可靠度曲线如图 3所示。由于(10)式涉及多重积分, 且被积函数难以用显示表达式表达, 只能采用数值方法进行计算, 下面将采用蒙特卡洛模拟方法给出近似解, 利用蒙特卡洛模拟的标准程序来评估近似解的精度[2]。
。根据(10)式, 得到相应的系统可靠度曲线如图 3所示。由于(10)式涉及多重积分, 且被积函数难以用显示表达式表达, 只能采用数值方法进行计算, 下面将采用蒙特卡洛模拟方法给出近似解, 利用蒙特卡洛模拟的标准程序来评估近似解的精度[2]。
 |
图 3 持续时间失效阈值服从β分布情形下系统可靠度曲线 |
2) 模型2下H(x1, x2)=k1x1+k2x2时系统可靠度
假设系统的警戒阈值、退化失效阈值和持续时间失效阈值分别为0.3,0.5和4.0, 其余参数取值与图 3相同。为了描述2个性能指标退化量的线性组合对系统可靠度的影响, 考虑k1和k2取不同参数值情形下的系统可靠度, 即: k1=1.5且k2=1.2、k1=1且k2=1、k1=0.5且k2=0.5、k1=0.4且k2=0.3、k1=1且k2=0。将可靠度曲线画在同一个图中, 如图 4所示, 其中k1=1且k2=0时的系统可靠度曲线可以看作一元随机退化系统的可靠度曲线。
 |
图 4 H(x1, x2)=k1x1+k2x2情形下系统可靠度曲线 |
从图 4可以发现, k1和k2的值越大, 系统的可靠度越低。这是因为k1和k2反映了2个性能指标退化量对系统整体退化量的贡献, 它们的值越大, 说明系统的退化速度越快, 从而系统的可靠度越低, 这与我们的直觉是一致的。另一个现象是, 当k1和k2的取值较小时, 其可靠度在退化过程的早期阶段高于单变量Wiener过程退化模型的结果, 而在退化过程的后期结果却相反, 这可以用2个性能指标的相关性(2个性能指标是负相关的)来解释。
3) 模型2下H(x1, x2)=|x1-x2|时系统可靠度分析
不等式|x1-x2|>L1曾被Cui等[8]用作平衡系统的失效准则, 即当2个性能指标退化量的距离大于失效阈值L1时, 系统失效; 采用Markov过程描述2个性能指标的退化过程, 并假设它们是相互独立的。下面, 利用算法1给出2个性能指标相关时采用函数H(x1, x2)=|x1-x2|描述系统退化程度情形下的系统可靠度曲线。假设τ=0, L1=0.1, 即只考虑单阶段退化过程。为了得到2个性能指标之间的相关性对系统可靠度的影响, 分别令ρ1=-0.8,-0.5,0,0.5和0.8, 将可靠度曲线画在同一个图中, 如图 5所示。其余参数取值与图 2相同。从图 5可以发现, 在其余参数值相同的情形下, 相关系数ρ1的值越大, 系统的可靠度越高。因此, 2个性能指标的退化过程是正相关(或负相关)时, 如果假设它们彼此独立, 则会低估(或高估)系统可靠度。
 |
图 5 模型2下H(x1, x2)=|x1-x2|时单阶段随机退化系统可靠度曲线 |
进一步, 为了探究持续时间失效阈值对系统可靠度的影响, 假设L1=0.1, L2=0.3, 其余参数取值与图 3相同, 考虑τ取不同参数值情形下的系统可靠度, 包括τ=0, 4, 7, 10和50, 并将可靠度曲线画在同一个图中, 如图 6所示。从图 6可以发现, 持续时间失效阈值越小, 系统的可靠度越低。这意味着系统处于缺陷阶段的可承受时间越短, 系统发生失效的可能性越大, 这与文献[20]的结论是一致的。
 |
图 6 模型2下H(x1, x2)=|x1-x2|时两阶段随机退化系统可靠度曲线 |
4 结论
本文针对二元随机退化系统,考虑性能指标融合以及竞争失效,提出了基于二元相关Wiener过程的退化模型,给出了性能指标不进行融合以及性能指标按照退化量的线性组合进行融合情形下,持续时间失效阈值为常数和随机变量时的系统可靠度的解析表达式。当性能指标按照任意形式进行融合时,提出了一个算法程序来模拟系统的可靠度。研究结果表明持续时间失效阈值越大,系统的可靠性越高。此外,当性能指标按照2个性能指标退化量的距离进行融合时,若2个性能指标正相关(或负相关)而假设它们彼此独立,则会低估(或高估)系统可靠度。因此,在工程实践中,如果存在2个(或多个)性能指标,应充分考虑它们的相关性,从而提高可靠性指标计算的精度。此外,本文给出的算法尽管能够用于性能指标按照任意形式进行融合情形下二元以及多元随机退化系统可靠度的模拟,但是由于该算法是基于蒙特卡洛模拟的,因此算法的精度强烈依赖于模拟次数,因此在今后研究中寻求系统可靠度的解析表达式以及其他算法将更加有意义。
References
- Ye Z S, Xie M. Stochastic modelling and analysis of degradation for highly reliable products[J]. Applied Stochastic Models in Business and Industry, 2015, 31(1):16–32 [Article] [Google Scholar]
- Zhao J B, Si S B, Cai Z Q. A multi-objective reliability optimization for reconfigurable systems considering components degradation[J]. Reliability Engineering & System Safety, 2019, 183: 104–115 [Article] [Google Scholar]
- Zhang F D, Ng H K T, Shi Y M. Mis-specification analysis of Wiener degradation models by using f-divergence with outliers[J]. Reliability Engineering & System Safety, 2019, 195: 106751 [Article] [Google Scholar]
- Zhang Z X, Si X S, Hu C H, et al. Degradation data analysis and remaining useful life estimation: a review on Wiener-process-based methods[J]. European Journal of Operational Research, 2018, 271(3):775–796 [Article] [Google Scholar]
- Hu Qiguo, Gao Zhan. A reliability evaluation method for system's dependent competition failure and multi-parameter degradation failure[J]. Journal of Northwestern Polytechnical University, 2019, 37(6):1191–1199 [Article] (in Chinese) [Google Scholar]
- Jiang R. A multivariate CBM model with a random and time-dependent failure threshold[J]. Reliability Engineering & System Safety, 2013, 119: 178–185 [Article] [Google Scholar]
- Yang Yuanjian. Research on reliability evaluation for mechanical products based on degradation modelling[D]. Chengdu: University of Electronic Science and Technology of China, 2016 (in Chinese) [Google Scholar]
- Cui L R, Chen J H, Li X C. Balanced reliability systems under Markov processes[J]. IISE Transactions, 2019, 51(9):1025–1035 [Article] [Google Scholar]
- Fu J C, Wu T L. Boundary crossing probabilities for high-dimensional Brownian motion[J]. Journal of Applied Probability, 2016, 53(2):543–553 [Article] [Google Scholar]
- Pan Z Q, Balakrishnan N, Sun Q, et al. Bivariate degradation analysis of products based on Wiener processes and copulas[J]. Journal of Statistical Computation and Simulation, 2013, 83(7):1316–1329 [Article] [Google Scholar]
- Yan Weian. Research on the method of storage reliability for torpedo[D]. Xi'an: Northwestern Polytechnical University, 2014 (in Chinese) [Google Scholar]
- Kong D J, Balakrishnan N, Cui L R. Two-phase degradation process model with abrupt jump at change point governed by Wiener process[J]. IEEE Trans on Reliability, 2017, 66(4):1345–1360 [Article] [Google Scholar]
- Wang X L, Jiang P, Guo B, et al. Real-time reliability evaluation for an individual product based on change-point gamma and Wiener process[J]. Quality and Reliability Engineering International, 2014, 30(4):513–525 [Article] [Google Scholar]
- Jiang R. Optimization of alarm threshold and sequential inspection scheme[J]. Reliability Engineering & System Safety, 2010, 95(3):208–215 [Article] [Google Scholar]
- Dong Q L, Cui L R, Si S B. Reliability and availability analysis of stochastic degradation systems based on bivariate Wiener processes[J]. Applied Mathematical Modelling, 2020, 79: 414–433 [Article] [Google Scholar]
- Wang W B. An overview of the recent advances in delay-time-based maintenance modelling[J]. Reliability Engineering & System Safety, 2012, 106: 165–178 [Article] [Google Scholar]
- Zhao X, Guo X X, Wang X Y. Reliability and maintenance policies for a two-stage shock model with self-healing mechanism[J]. Reliability Engineering & System Safety, 2018, 172: 185–194 [Article] [Google Scholar]
- Zhang S, Lyu R N, Si S B, et al. Reliability analysis of systems with common cause failure based on stress-strength interference model[J]. Journal of Shanghai Jiaotong University, 2018, 23(5):707–710 [Article] [Google Scholar]
- Zhu W J, Fouladirad M, BÉRenguer C. Multi-level maintenance policy based on a multi-component system with two independent failure modes[J]. Reliability Engineering & System Safety, 2016, 153: 50–63 [Article] [Google Scholar]
- Dong Q L, Cui L R. A study on stochastic degradation process models under different types of failure thresholds[J]. Reliability Engineering & System Safety, 2019, 181: 202–212 [Article] [Google Scholar]
- Qiu Q A, Cui L R. Reliability evaluation based on a dependent two-stage failure process with competing failures[J]. Applied Mathematical Modelling, 2018, 64: 699–712 [Article] [Google Scholar]
- Yang L, Ma X B, Zhao Y. A condition-based maintenance model for a three-state system subject to degradation and environmental shocks[J]. Computers & Industrial Engineering, 2017, 105: 210–222 [Article] [Google Scholar]
- Liu T Y, Pan Z Q, Sun Q, et al. Residual useful life estimation for products with two performance characteristics based on a bivariate Wiener process[J]. Journal of Risk and Reliability, 2017, 231(1):69 80 [Article] [Google Scholar]
- Zhang Y, Jia X, Guo B. Bayesian framework for satellite rechargeable lithium battery synthesizing bivariate degradation and lifetime data[J]. Journal of Central South University, 2018, 25(2):418–431 [Article] [Google Scholar]
- Xu A C, Shen L J, Wang B X, et al. On modeling bivariate Wiener degradation process[J]. IEEE Trans on Reliability, 2018, 67(3):897–906 [Article] [Google Scholar]
- Duan F J, Wang G J, Wang H. Inverse Gaussian process models for bivariate degradation analysis: a Bayesian perspective[J]. Communications in Statistics-Simulation and Computation, 2018, 47(1):166–186 [Article] [Google Scholar]
- Sacerdote L, Tamborrino M, Zucca C. First passage times of two-dimensional correlated processes: analytical results for the Wiener process and a numerical method for diffusion processes[J]. Journal of Computational and Applied Mathematics, 2016, 296: 275–292 [Article] [Google Scholar]
All Figures
 |
图 1 模型1下系统的退化路径 |
| In the text | |
 |
图 2 模型1下基于模拟解和解析解的系统度曲线 |
| In the text | |
 |
图 3 持续时间失效阈值服从β分布情形下系统可靠度曲线 |
| In the text | |
 |
图 4 H(x1, x2)=k1x1+k2x2情形下系统可靠度曲线 |
| In the text | |
 |
图 5 模型2下H(x1, x2)=|x1-x2|时单阶段随机退化系统可靠度曲线 |
| In the text | |
 |
图 6 模型2下H(x1, x2)=|x1-x2|时两阶段随机退化系统可靠度曲线 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


