| Issue |
JNWPU
Volume 42, Number 1, February 2024
|
|
|---|---|---|
| Page(s) | 165 - 172 | |
| DOI | https://doi.org/10.1051/jnwpu/20244210165 | |
| Published online | 29 March 2024 | |
Residence-times distribution function of a periodically modulated bistable system subject to noise recycling
循环噪声作用下周期调制双稳系统的驻留时间分布函数
1
School of Mathematics and Statistics, Northwestern Polytechnical University, Xi'an 710129, China
2
School of Math & Information Technology, Yuncheng University, Yuncheng 044000, China
Received:
10
March
2023
The research mentioned in the statement focuses on investigating a theoretical method for calculating the residence-times distribution function (RTDF) in a periodically driven, bistable system subject to noise recycling. This situation deviates from a Markovian process due to the recycling lag, making it challenging to determine the RTDF using traditional two-state models. In this paper, the aim is to overcome this issue and provide a systematic analysis of how to calculate the RTDF in such a system. By considering the piecewise escape rate of the system, which relies not only on the current state but also on the previous state, we have successfully derived the recursive expression of RTDF. Then, RTDF for large and small A/D is approximately derived using a piecewise analysis formula, respectively. It is further demonstrated both theoretically and numerically that the RTDF has exhibited a feedback-induced structure as a result of the recycling procedure. The results are shown as follows: for large A/D, the RTDF exhibits a series of sharp peaks located at odd multiples of approximately half the period of the driving signal. This indicates the occurrence of stochastic resonance. Additionally, it is interesting to note that the RTDF displays a sharp dip at t=τ. It is further shown that the process of noise recycling increases the probability of short residence times for t < τ and decreases the probability of long residence times for t>τ. This demonstrates that noise recycling plays a crucial role in facilitating particle hops between the double-well potential. For small A/D, the RTDF displays a phenomenon of piecewise exponential decay and declines sharply at t=τ. Notably, the interval between discontinuities becomes smaller or even disappears with increasing the noise intensity or the relative strength. Furthermore, when driven by an appropriate periodic signal, the RTDF exhibits a sequence of maximum values at odd multiples of approximately half the period of the driving signal. However, these maximum values disappear with increasing the noise intensity or the relative strength. This suggests that moderate noise recycling can induce the occurrence of stochastic resonance. However, excessive noise recycling actually inhibits the generation of stochastic resonance. The theoretical results have been successfully validated via numerical methods, demonstrating the reasonability of the present theoretical approach.
摘要
提出了一种计算循环噪声作用下周期调制双稳系统驻留时间分布函数的理论方法。基于具有分段逃逸速率的两态模型理论, 建立粒子逃逸的瞬时速率方程, 推导得出驻留时间分布函数的递归表达式。基于此, 分别计算信号振幅与循环噪声强度比值较大和较小2种不同情形下驻留时间分布函数的解析表达式。并且, 从理论和数值模拟两方面分别阐明了循环噪声对驻留时间分布函数结构的影响。研究结果表明: 驻留时间分布函数呈现指数衰减且在循环滞后时间处出现骤然下降趋势, 且随着噪声强度和相关强度的增大驻留时间分布函数衰减速度变快, 说明循环噪声能够加速粒子在势阱间的跃迁。此外, 在周期信号的调制下, 驻留时间分布函数在信号半周期的奇数倍处出现一系列峰值, 这预示着系统发生了随机共振现象。
Key words: noise recycling / periodically modulated bistable system / residence-times distribution function / stochastic resonance
关键字 : 循环噪声 / 周期调制双稳系统 / 驻留时间分布函数 / 随机共振
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
自随机共振[1]的概念提出之后, 人们意识到噪声在非线性科学领域能够起到建设性作用。然而, Goulding等[2]通过实验发现当噪声在系统中传输时可分裂成多个含有时滞且具有时间关联性的同源噪声, 这类噪声被称为“循环噪声”[3]。循环噪声能够影响非线性系统的动力学行为, 如诱导双稳系统的随机同步[4]、控制可激系统的随机脉冲运动[5]、控制Brusselator模型的相干共振[6]、诱导Birhythmic系统的随机分岔等[7]。特别地, Sun等[8-9]阐明了循环噪声能够诱导双稳系统以及时滞双稳系统发生随机共振现象。循环噪声在通信领域应用较为广泛, 能有效改善通信系统中的区块误码率[10], 显著提高正交信道的解码性能[11]。
近几十年, 研究者们提出了一些经典指标来进一步刻画随机共振现象, 包括信噪比[12]、线性响应[13]、驻留时间分布函数[14]。作为其中的一个衡量指标, 驻留时间分布函数最早由Gammaitoni等[15]提出, 并将粒子在左右对称的势阱中发生连续2次跃迁事件的时间间隔分布定义为驻留时间分布。随后Zhou等[16]开创了一种用来计算在弱周期信号驱动下双稳系统驻留时间分布函数的近似方法, 并说明了在外部驱动力半周期的奇数倍时驻留时间分布函数呈现一系列峰值, 即系统发生了随机共振现象。进一步地, Masoller[17]将该方法推广到时滞双稳系统中, 且从理论和数值方面分别阐明了驻留时间分布函数曲线在时滞处呈现陡然上升或骤然下降的趋势。Curtin等[18]采用垂直腔面发射激光器从实验角度验证了时滞双稳系统中驻留时间分布函数的特殊结构, 与前期的理论结果十分吻合。最近, Sun等[19-20]提出了一种计算循环噪声驱动下双稳系统驻留时间分布函数的理论方法, 并用数值方法验证了该理论方法的可行性。然而, 针对耦合外部周期驱动力和循环噪声的双稳系统, 其驻留时间分布函数的研究还未被涉及。
鉴于此, 本文主要探讨循环噪声作用下周期调制双稳系统驻留时间分布函数的理论计算方法。考虑过阻尼粒子在系统的双势阱中运动, 其朗之万方程为
且
式中: Asin(ωt+ϕ)是外部周期驱动力;A表示振幅; ω表示频率; ϕ表示相位。此外, D表示噪声强度; ε表示相关强度;τ表示循环滞后时间。(2)式中的ζ(t)表示循环噪声, 是由高斯白噪声ξ(t) (主噪声)和噪声循环项εξ(t-τ)(第二噪声)构成的, 且满足
因此, 得出关于循环噪声的统计性质为
1 逃逸速率和驻留时间分布函数理论
不失一般性, 假设粒子运动的初始时刻是t0=0且粒子处在右势阱中。在不含有外部驱动力时, 对于ε≠0以及一个适当大的时滞τ,当0≤t≤τ时, 假设ξ(t)和εξ(t-τ)完全不相关。因此, 此时粒子的逃逸速率可由克拉默法则得出, 即r= 。
。
为了便于表述, 首先引入一些符号: “∓”表示系统的左右势阱, W±(t)表示在无外部摄动的系统(A=0)中粒子逃出“∓”的逃逸速率, W±(t)表示在模型(1)中粒子逃出“∓”的速率。由文献[16]可得
式中,D=D(1+ε2)。此外, 由文献[19]建立的两态模型可推出W±(t)的递归表达式为:
式中
及
式中:0≤t < τ;n=1, 2…。
引入p+(t)(p-(t))表示粒子在右(左)势阱的概率, 则粒子的瞬时逃逸速率方程为
为了计算驻留时间分布函数, 首先应考虑粒子的逃逸时间分布函数。由于逃逸时间分布函数依赖于驱动周期的初相位ϕ, 不妨采用ρ±(t/ϕ)表示粒子的逃逸时间分布函数, 且有
式中,Z是归一化常数。
假设逃逸事件是瞬时发生的, 则粒子逃出“±”势阱的相位分布Y±(ϕ)为
式中,I0(x)是修正贝塞尔函数。因此驻留时间分布函数为
式中,Z是归一化常数且满足 。
。
简化之, 仅计算粒子在右势阱的驻留时间分布函数。对于nτ≤t < (n+1)τ, n=0, 1…, (13)式的解为
由(14)式和(17)式可推导出逃逸时间分布函数的递归表达式为
式中,Z是归一化常数。由(16)式和(18)式可得驻留时间分布函数的递归表达式为
式中,Z是归一化常数且满足
 。
。
2 较大A/D情形下的驻留时间分布函数
为了进一步了解驻留时间分布函数的结构, 首先计算A/D较大时驻留时间分布函数的近似解析表达式, 并基于此讨论其结构特性。
2.1 理论计算
对于较大的A/D, 当0≤t < τ时, 粒子逃出右势阱的逃逸速率可近似为
由(13)式经过一系列的计算可得驻留时间分布函数为
式中: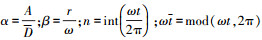 ;erf(x)是误差函数。
;erf(x)是误差函数。
当τ≤t+τ < 2τ时, 根据(5)式和(7)式, 逃逸速率可近似为
令t1=t+τ, 且将(22)式代入(17)式得
令 
对于α→∞, exp[-αsin(θ+ϕ)]在θ+ϕ=  处取极大值, 因此由高斯近似[21]可得
处取极大值, 因此由高斯近似[21]可得
通过计算得
式中, 。
。
因此
式中
且  。由(18)式可得
。由(18)式可得
对于A/D→∞, Y+(ϕ)在  处取极大值, 因此当τ≤t1 < 2τ时, 驻留时间分布函数的解析表达式可近似为
处取极大值, 因此当τ≤t1 < 2τ时, 驻留时间分布函数的解析表达式可近似为
式中
2.2 结果分析
如图 1所示,固定参数D=0.04, A=0.15, ω=0.05, ε=0.3, 发现在  , n=0, 1, 2…处(其中T表示外部驱动力的周期), 驻留时间分布函数呈现一系列的峰值, 说明系统发生了随机共振现象。此外, 值得注意的是驻留时间分布函数在t=τ处骤然下降, 呈现出明显的间断性。
, n=0, 1, 2…处(其中T表示外部驱动力的周期), 驻留时间分布函数呈现一系列的峰值, 说明系统发生了随机共振现象。此外, 值得注意的是驻留时间分布函数在t=τ处骤然下降, 呈现出明显的间断性。
为了进一步了解循环噪声对驻留时间分布函数结构产生的影响, 将含有噪声循环过程的驻留时间分布函数结构与不含有第二噪声项的驻留时间分布函数结构进行对比。如图 2所示,设定参数D=0.04, A=0.15, ω=0.05, ε=0.3, τ=300(实线)和D=0.04, A=0.15, ω=0.05, ε=0(虚线), 其中图 2a)表示理论结果, 图 2b)表示数值结果。通过对比发现, 当t < τ时, 在循环噪声作用下驻留时间分布函数的峰值变大, 然而, 当t>τ时, 却与之相反。这说明当t < τ时循环噪声能够增强随机共振效应, 当t>τ时, 由于循环噪声的驱动随机共振效应相对减弱。
 |
图1 驻留时间分布函数理论结果(实线)和数值模拟结果(D=0.04, A=0.15, ω=0.05, ε=0.3, τ=300) |
 |
图2 τ=300和τ=0的驻留时间分布函数(D=0.04, A=0.15, ω=0.05, ε=0) |
3 较小A/D情形下的驻留时间分布函数
3.1 理论计算
在较小A/D情形下, 当0≤t < τ时, 粒子逃出右势阱的逃逸速率可近似为
将初始条件p+(t0=0)=1与(33)式代入(17)式可得
在较小A/D的情形下, 修正贝塞尔函数I0(A/D)可近似为
取到A/D的二次项, I0(A/D)可近似为
由(19)式可得当0≤t < τ时, 驻留时间分布函数的解析表达式为
当τ≤t+τ < 2τ时, 不妨设t1=t+τ, 则τ≤t1 < 2τ。将t1=t+τ代入(5)式和(7)式可近似得到
通过一系列的计算, 当τ≤t1 < 2τ时, 驻留时间分布函数的解析表达式为
式中
且
3.2 结果分析
固定参数D=0.07, A=0.06, ε=0.4, τ=200, 根据(37)式和(39)式所得的驻留时间分布函数的解析结果与数值模拟结果如图 3所示。
从图 3中可以看到驻留时间分布函数呈分段指数衰减, 且在t=τ处出现骤然下降现象, 呈现出明显的间断性。另外, 在 , n=0, 1, 2…处(其中T表示外部驱动力的周期)驻留时间分布函数出现了极大值, 这预示着随机共振现象的发生。
, n=0, 1, 2…处(其中T表示外部驱动力的周期)驻留时间分布函数出现了极大值, 这预示着随机共振现象的发生。
 |
图3 随w变化的驻留时间分布函数的理论结果和数值模拟结果(D=0.07, A=0.06, ε=0.4, τ=200) |
3.2.1 噪声强度的影响
取参数A=0.06, ω=0.1, ε=0.5, τ=150, 如图 4所示: 当噪声强度D适当变化时, 驻留时间分布函数曲线具有分段衰减变化趋势, 且在t=τ处出现间断。随着D的增大, 在t=τ处间断的间距逐渐变小乃至于消失。如图 4d)所示, 驻留时间分布函数曲线开始单调地指数衰减, 这说明了较大的噪声强度D使得主噪声项和第二噪声项之间不再具有相关性, 即驻留时间分布函数的结构可近似地由(37)式决定。此外, 驻留时间分布函数衰退速率随着D的增大而加快, 说明了循环噪声可以加速粒子的跃迁。
 |
图4 随D变化的驻留时间分布函数的理论结果和数值模拟结果(A=0.06, ω=0.1, ε=0.5, τ=150) |
3.2.2 相关强度的影响
将参数D=0.07, A=0.05, ω=0.15, τ=200固定, 不同相关强度如ε=0, ε=0.3, ε=0.7以及ε=1的驻留时间分布函数如图 5所示。从图 5a)~5b)可以发现在 , n=0, 1, 2…处(T表示外部驱动力的周期), 驻留时间分布函数出现峰值, 即系统产生了随机共振效应。对比图 5a)~5b), 发现当系统具有第二噪声项时, 驻留时间分布函数在t=τ处出现明显间断。此外, 驻留时间分布函数的峰值随着相关强度ε的增大逐渐变弱, 甚至消失, 如图 5c)~5d)所示, 这说明了较大的相关强度ε可抑制随机共振效应。同时, 驻留时间分布函数的衰退速率随着相关强度ε的增大而加快, 说明在较大强度的循环噪声能够缩短粒子在某个势阱的驻留时间, 即加剧了粒子的逃逸运动。
, n=0, 1, 2…处(T表示外部驱动力的周期), 驻留时间分布函数出现峰值, 即系统产生了随机共振效应。对比图 5a)~5b), 发现当系统具有第二噪声项时, 驻留时间分布函数在t=τ处出现明显间断。此外, 驻留时间分布函数的峰值随着相关强度ε的增大逐渐变弱, 甚至消失, 如图 5c)~5d)所示, 这说明了较大的相关强度ε可抑制随机共振效应。同时, 驻留时间分布函数的衰退速率随着相关强度ε的增大而加快, 说明在较大强度的循环噪声能够缩短粒子在某个势阱的驻留时间, 即加剧了粒子的逃逸运动。
 |
图5 随ε变化的驻留时间分布函数的理论结果和数值模拟结果(D=0.07, A=0.05, ω=0.15, τ=200) |
4 结论
本文主要提供了一种计算耦合周期信号和循环噪声的双稳系统驻留时间分布函数的理论方法。基于具有分段逃逸速率的两态模型, 推导出逃逸时间分布函数和驻留时间分布函数的递归表达式。在此基础上, 运用近似方法, 分别给出较大A/D和较小A/D这2种情形下0≤t < τ和τ≤t1 < 2τ驻留时间分布函数的解析表达式。从理论和数值两方面对驻留时间分布函数进行分析, 二者吻合性较好, 充分验证了理论计算方法的有效性, 且该计算方法可推广到t>2τ的情形。此外, 从理论和数值两方面论证了循环噪声对驻留时间分布函数结构的影响: 对于较大的A/D, 驻留时间分布函数呈现指数衰减现象且在t=τ处出现明显间断, 且当t < τ时循环噪声能够增强随机共振效应, 而当t>τ时, 随机共振效应相对减弱。对于较小的A/D, 驻留时间分布函数呈现指数衰减现象且在t=τ处出现间断, 随着噪声强度和相关强度的增加间断性逐渐减小甚至消失。特别地, 循环噪声在某种程度上可以抑制随机共振的发生。本文研究方法可用于计算耦合时滞的周期调制双稳系统的驻留时间分布函数。
References
- BENZI R, SUTERA A, VULPIANI A. The mechanism of stochastic resonance[J]. Journal of Physics A: Mathematical and General, 1981, 14(11): L453. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- GOULDING D, MELNIK S, CURTIN D, et al. Kramers' law for a bistable system with time-delayed noise[J]. Physical Review E, 2007, 76(3): 031128. [Article] [CrossRef] [Google Scholar]
- BORROMEO M, GIUSEPPONI S, MARCHESONI F. Recycled noise rectification: an automated Maxwell's daemon[J]. Physical Review E, 2006, 74(3): 031121. [Article] [CrossRef] [Google Scholar]
- BORROMEO M, MARCHESONI F. Stochastic synchronization via noise recycling[J]. Physical Review E, 2007, 75(4): 041106. [Article] [CrossRef] [Google Scholar]
- MA J, GAO Q Y. Control of stochastic spike motion in an excitable system via recycled noise[J]. Science China Chemistry, 2011, 54: 1504–1509. [Article] [CrossRef] [Google Scholar]
- MA J, HOU Z H, XIN H W. Control coherence resonance by noise recycling[J]. The European Physical Journal B, 2009, 69: 101–107. [Article] [CrossRef] [Google Scholar]
- CHÉAGÉ C A, YAMAPI R, WOAFO P. Bifurcations in a birhythmic biological system with time-delayed noise[J]. Nonlinear Dynamics, 2013, 73: 2157–2173. [Article] [CrossRef] [Google Scholar]
- SUN Z K, YANG X L, XU W. Resonance dynamics evoked via noise recycling procedure[J]. Physical Review E, 2012, 85(6): 061125. [Article] [CrossRef] [Google Scholar]
- SUN Z K, YANG X L, XIAO Y Z, et al. Modulating resonance behaviors by noise recycling in bistable systems with time delay[J]. Chaos, 2014, 24: 023126. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- COHEN A, SOLOMON A, DUFFY K R, et al. Noise recycling[C]//IEEE International Symposium on Information Theory, Los Angeles, CA, USA, 2020: 315–320 [Google Scholar]
- RIAZ A, SOLOMON A, ERCAN F, et al. Interleaved noise recycling using GRAND[C]//IEEE International Conference on Communications, Seoul, 2022: 2483–2488 [Google Scholar]
- XU P F, JIN Y F. Stochastic resonance in an asymmetric tristable system driven by correlated noises[J]. Applied Mathematical Modelling, 2020, 77: 408–425. [Article] [CrossRef] [Google Scholar]
- WORMELL C L, GOTTWALD G A. On the validity of linear response theory in high-dimensional deterministic dynamical systems[J]. Journal of Statistical Physics, 2018, 172: 1479–1498. [Article] [NASA ADS] [CrossRef] [Google Scholar]
- DAVIS D, TROIANO M, CHINNICI A, et al. Particle residence time distributions in a vortex-based solar particle receiver-reactor: an experimental, numerical and theoretical study[J]. Chemical Engineering Science, 2020, 214: 115421. [Article] [CrossRef] [Google Scholar]
- GAMMAITONI L, MARCHESONI F, MENICHELLA-SAETTA E, et al. Stochastic resonance in bistable systems[J]. Physical Review Letters, 1989, 62(4): 349–352. [Article] [CrossRef] [Google Scholar]
- ZHOU T, MOSS F, JUNG P. Escape-time distributions of a periodically modulated bistable system with noise[J]. Physical Review A, 1990, 42(6): 3161. [Article] [CrossRef] [Google Scholar]
- MASOLLER C. Distribution of residence times of time-delayed bistable systems driven by noise[J]. Physical Review Letters, 2003, 90(2): 020601. [Article] [CrossRef] [Google Scholar]
- CURTIN D, HEGARTY S P, GOULDING D, et al. Distribution of residence times in bistable noisy systems with time-delayed feedback[J]. Physical Review E, 2004, 70(3): 031103. [Article] [CrossRef] [Google Scholar]
- SUN Z K, WU Y Z, DU L, et al. Residence-times distribution function of bistable system subjected to noise recycling[J]. Nonlinear Dynamics, 2016, 84: 1011–1019. [Article] [CrossRef] [Google Scholar]
- WU Yazhen, SUN Zhongkui. Residence-times distribution function in asymmetric bistable system driven by noise recycling[J]. Acta Physica Sinica, 2020, 69(12): 2–11. [Article] (in Chinese) [Google Scholar]
- CHUNG S Y, RICHARDSON T J, URBANKE R L. Analysis of sum-product decoding of low-density parity-check codes using a Gaussian approximation[J]. IEEE Trans on Information Theory, 2001, 47(2): 657–670. [Article] [Google Scholar]
All Figures
 |
图1 驻留时间分布函数理论结果(实线)和数值模拟结果(D=0.04, A=0.15, ω=0.05, ε=0.3, τ=300) |
| In the text | |
 |
图2 τ=300和τ=0的驻留时间分布函数(D=0.04, A=0.15, ω=0.05, ε=0) |
| In the text | |
 |
图3 随w变化的驻留时间分布函数的理论结果和数值模拟结果(D=0.07, A=0.06, ε=0.4, τ=200) |
| In the text | |
 |
图4 随D变化的驻留时间分布函数的理论结果和数值模拟结果(A=0.06, ω=0.1, ε=0.5, τ=150) |
| In the text | |
 |
图5 随ε变化的驻留时间分布函数的理论结果和数值模拟结果(D=0.07, A=0.05, ω=0.15, τ=200) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


