| Issue |
JNWPU
Volume 42, Number 2, April 2024
|
|
|---|---|---|
| Page(s) | 251 - 259 | |
| DOI | https://doi.org/10.1051/jnwpu/20244220251 | |
| Published online | 30 May 2024 | |
Performance and influencing factors of acoustic grating based on signal enhancement
声栅结构信号增强性能及其影响因素研究
1
School of Marine Science and Technology, Northwestern Polytechnical University, Xi'an 710072, China
2
No.705 Research Institute of China State Shipbuilding Corporation Limited, Xi'an 710069, China
Received:
14
February
2023
In the acoustic signal receiving section of underwater vehicle, an effective measure to improve surface acoustic impedance and reduce signal attenuation is to cover acoustic barrier plate of hydrophone array with high impedance material (signal conditioning plate). Compared with traditional full coverage mode, an acoustic grating (periodic installation of regulator plate array) can greatly improve the received signal gain and reduce the weight of the receiving segment. In order to deeply understand the signal enhancement mechanism and optimize the design of acoustic grating, the factors that influence the signal enhancement performance of acoustic grating from the aspects of width, thickness, incident angle and structure width ratio is studied. Simulation results show that the oblique incidence will change the symmetrical distribution of signal ratio (SR), but will not significantly change the acoustic performance of the structure. Wider and thicker regulating plate lead to stronger non-mirror scattering and better signal enhancement performance of structure. In practical application, geometric parameters of acoustic grating should be reasonably designed to meet multiple constraints of real environment to achieve optimal overall performance. In addition, the moderate width ratio can obtain a good overall acoustic performance.
摘要
对于安装在水下航行器声信号接收段的水听器阵列, 在其声障板上覆盖高声阻抗材料(称为信号调节板)是一种能有效提高表面声阻抗并减少信号衰减的措施。相比传统的完全覆盖方式, 声栅结构(即周期性地敷设调节板阵列)可以极大地提高接收信号增益, 减小接收段的质量。为了深入理解声栅结构信号增强机理, 优化声栅结构设计, 研究了调节板宽度、调节板厚度、入射角以及结构宽度比等因素对声栅结构信号增强性能的影响。仿真结果表明: 斜入射会改变信号比(SR)的对称分布, 但不会大幅改变结构的声学性能; 调节板越宽、越厚, 引起的非镜面散射会更强, 声栅结构的信号增强性能就越好。在实际应用中, 应合理设计声栅结构几何参数以满足现实环境的多重约束以达到总体性能最优, 此外适中的宽度比能获得良好的总体声学性能。
Key words: signal enhancement / signal conditioning plate / limited space / acoustic grating / lightweight / acoustic focusing
关键字 : 信号增强 / 信号调节板 / 有限空间 / 声栅 / 轻量化 / 声聚焦
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
声呐是水中目标探测和通讯的主要设备, 其中水听器阵列通常安装在水下航行器内部的声信号接收段, 因此会收到来自后方结构中的弯曲波噪声。将水听器安装在距振动表面一定距离处能够有效降低这种由振动引起的噪声(即结构噪声), 该距离被称为隔振距离[1]。对于某些必须直接安装在耐压船体上的水听器阵列来说[2], 结构噪声的控制尤为困难, 一般需借助在航行器表面敷设声学覆盖层解决。
在声呐系统的换能器分系统中, 反声障板具有隔离航行器本体辐射噪声、提高接收空间增益的功能[3]。由于障板与海水的特性声阻抗差异较大, 声波在两界面间传播时阻抗失配, 从而能够达到良好的声反射效果[4], 同时也会反射具有显著相位变化的声波, 进而降低水听器处的总信号。为此, 需要在障板上再加一层高声阻抗材料(亦称为信号调节板)以提高表面阻抗并减少信号衰减。传统上, 信号调节板会完全覆盖航行器表面, 但这会极大地增加结构的厚度与质量, 在实际应用中限制较大。
Zhang等[5-6]提出了声栅结构, 即由信号调节板组成的阵列结构能够产生局域信号反射从而增加障板上水听器的信号比, 其效果优于完全覆盖的信号调节板, 同时不影响覆盖层结构的整体声吸收。但其研究仅针对理想情况下的无限大结构且未对信号增强性能的影响参数进行深入分析。
一个多世纪以来, 关于声波在声栅上的散射和吸收已有不少相关研究, 学者们采用各种方法模拟声栅不同结构参数的影响, 例如声栅的刚度、形状等[7-8]。大多数研究都是基于刚性、压力释放或周期表面的局域反应等假设, 声栅的弹性特性往往被忽略。然而, 在存在流体载荷且流体-结构相互作用强烈的情况下, 弹性表面的振动对散射声场的影响可能会变得非常显著[9-10]。另一方面, 在小型水下航行器信号接收段中, 实际安装的声栅, 其几何参数和质量等参数受到多种限制。
因此, 针对水下航行器信号接收段形成的小空间, 本文在静止流体-结构耦合作用基础上, 对单周期和多周期声栅的信号增强结构进行建模, 仿真分析了结构的声学性能及其影响因素。研究了调节板宽度、调节板厚度、入射角以及结构宽度对声栅结构信号增强性能的影响, 为声栅结构设计与优化提供理论指导。
1 声栅结构模型及其性能指标
信号调节板是一种尺寸有限的均质薄板, 而声栅是周期性排列的信号调节板阵列。图 1给出了声栅结构的横截面, 主要包括基板、弹性覆盖层和信号调节板阵列。结构上方为静止流体(水), 下方为空气; 假设激励为远场入射的平面波, 板、覆盖层和所有信号调节板在Y轴方向上无限远, 因此只需要对X-Z二维截面上的振动和辐射声进行理论建模。
为了更清晰地分析同一空间位置下总声场相对于入射声场的增强幅度, 对声栅结构上方的总声压进行归一化处理。为此, 引入判断信号增强的主要参量为信号比(signal ratio, SR), 即将总声压与入射声压之比以对数的形式表示
式中: pi(x, z)=Pie-jk0(xsinθi-zcosθi)为入射声压; pT为入射声产生的总声信号, 它可以表示为
式中,pb(x, z)为阻塞声压(blocked pressure), 由入射声压及其镜面反射叠加而成, 有
式中:Pi为入射声压幅值;k0为水介质中的波数;θi为入射仰角。
另一方面, ps(x, z)为散射声压, 可以分为两部分: 一部分是均匀覆盖层板的镜面反射声pC(x, z)
式中:ρ0为水密度;ω为入射声波角频率;a0, F21, α, F22和G都是k0sinθi的函数。另一部分是周期性信号调节板产生的额外散射声pSCPs(x, z)
式中: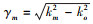 是上半空间在z方向上的声波数;
是上半空间在z方向上的声波数; 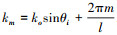 , m是空间谐波序号; l是表面的空间周期。
, m是空间谐波序号; l是表面的空间周期。
当位置(x, z)和入射波频率f确定后, pb(x, z)和pC(x, z)仅仅是入射角θi的函数, 因此调节板产生的额外散射声pSCPs(x, z)是调节板上信号增强的关键, 也是SR的主要贡献量。然而, 在pSCPs(x, z)的表达式中, Pscpsm十分复杂, 与很多参数有关, 包括一些结构参数, 如调节板的尺寸、构型等。虽然文献[5]中给出了Pscpsm的计算表达式, 但计算过程十分复杂, 难以通过理论公式量化分析这些结构参数的具体影响。本文建立声栅结构的有限元仿真模型, 分析入射角θi以及结构参数对声栅信号增强性能的影响。
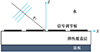 |
图1 周期性声栅复合结构 |
2 单周期声栅结构声学性能及其影响因素
周期性声栅由若干个声栅单元构成, 为了便于分析, 首先对单周期声栅结构的声学性能进行计算机仿真, 研究不同因素对单周期声栅结构声学性能的影响。
2.1 单周期声栅结构建模
通过声学仿真软件COMSOL建立声栅结构有限元模型, 分析该声栅结构的声场分布。在小型水下航行器中, 反声障板一般采用圆盘形, 为此建立半径为0.1 m的圆盘基板, 在其上方覆盖相同尺寸的弹性覆盖层得到覆盖层障板结构, 基板和覆盖层厚度均为0.01 m。结构上方添加圆柱形水域, 下方介质为空气域, 厚度均为0.05 m。在结构上方沿Y轴敷设一个单周期声栅, 信号调节板为条形薄板, 厚度为0.007 5 m, 宽度为0.1 m, 调节板外侧与障板对齐。在介质外部添加完美匹配层, 模拟无反射的吸收场; 在水域中添加背景压力场, 设置幅值Pi=1 Pa平面波垂直入射作为激励; 覆盖层障板结构四周自由。由于模型、声场呈对称分布, 通过施加对称边界条件, 计算1/4模型即可分析结构的声学性能, 如图 2所示。
利用声-固耦合作为边界条件, 选择频域分析以确定SR的空间分布特征。基板及信号调节板作为质量层, 以钢作为材料。弹性覆盖层为橡胶材质, 在仿真软件中基于弹性假设, 给出覆盖层横波和纵波波速作为材料参数, 分别为 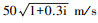 以及
以及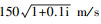 , 在仿真中将横波、纵波波速转为材料的杨氏模量与泊松比[2]。将薄板理论应用于声场-结构相互作用的分析, 假设: ①流体和结构都是均匀的, 并且服从线性本构方程; ②薄板中存在摩擦耗散引起的损耗因子; ③薄板的法向位移在整个板厚度上是均匀的。但需要注意的是, 使用薄板理论时获得的数值结果在其吻合频率(coincidence frequency)以下才有效。对于薄板来说, 其吻合频率为[11]
, 在仿真中将横波、纵波波速转为材料的杨氏模量与泊松比[2]。将薄板理论应用于声场-结构相互作用的分析, 假设: ①流体和结构都是均匀的, 并且服从线性本构方程; ②薄板中存在摩擦耗散引起的损耗因子; ③薄板的法向位移在整个板厚度上是均匀的。但需要注意的是, 使用薄板理论时获得的数值结果在其吻合频率(coincidence frequency)以下才有效。对于薄板来说, 其吻合频率为[11]
式中:c为流体声速; h为薄板厚度;ρ, E, υ分别为薄板的密度、杨氏模量以及泊松比。假定流体(水)中声速为c=1 460 m/s, 则0.01 m厚、材料为钢(ρ=7 800 kg/m3, E=21.6×1010 N/m3, υ=0.3)的基板, 其吻合频率为21.3 kHz。因此软件中对声栅结构的频域仿真在21.3 kHz以下, 以100 Hz为步长进行。
文献[5]利用平均吸声系数验证了模型的正确性。根据(1)式在仿真中采用(7)式计算信号比
式中:Lpt为总声压级;Lpb为背景声压级。
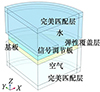 |
图2 单周期声栅结构仿真模型 |
2.2 声栅结构的声学性能
为了对声栅的声学性能进行分析, 将X轴(结构宽度方向), 以及沿Y轴(结构长度方向)选取的若干条截线作为数据集, 并在后文中沿用该选取方式。Y轴方向截线均匀选择结构有代表性的位置, 包括信号调节板的中心(截线1)、1/4处(截线2, 3)、边缘(截线4, 5), 未敷设调节板的覆盖层中心(截线6, 7)以及边缘(截线8, 9), 各截线的位置以及标号如图 3所示。信号调节板上方的局域信号增强是判断声栅性能的重要依据, 后文重点对结构宽度方向的信号比分布特征进行分析。
为了分析SR随频率变化的规律, 对Y轴截线上的SR进行平均。在法向入射平面波激励下, 声场呈对称分布, 只需选取截线1, 3, 5, 7, 9计算平均SR。通过与无声栅障板进行对比, 分析信号的增益效果。图 4给出了不同Y轴截线的平均SR频率分布。
与无声栅相比, 声栅结构改变了SR无规则的分布, 使其具有明显的局域分布特征, 调节板表面的平均SR在宽频带范围内有显著增强, 仅在1 kHz附近的窄带小于无声栅情况, 这是由于非镜面散射声压与其余声压成分的相位相反导致[5]。调节板中心与1/4处的平均SR在3 kHz以上时大于零, 调节板表面的入射信号在宽频带内得到了增强。平均SR在3.8, 18.4以及19.4 kHz, 即捕获模态频率[12]时达到峰值, 最高能够达到13.1 dB的信号增益; 调节板边缘的平均SR稍低, 信号增强性能较差。未敷设调节板的区域信号无明显增强, 覆盖层中心的平均SR分布与无声栅结构基本吻合。由于水听器安装在调节板上, 因此后文只关心调节板表面上的信号增强。在水声学中, 不同应用领域声信号频率高低的划分不一样。本文研究针对的是水下航行器声探测任务, 且声信号频率上限为21.3 kHz, 为了更好地分析声栅结构对不同频率范围内信号的增强性能, 以及后续研究各因素对不同频率范围信号增强性能影响, 本文将2 kHz以下作为低频, (2~10)kHz作为中频, 10 kHz以上作为高频。
分析SR在结构宽度方向上的空间分布特征, 计算隔振距离为0.007 5 m时X轴上的SR分布, 结果如图 5所示, 其中横坐标范围(-0.05, 0.05)为信号调节板所在空间, 纵坐标为频率, 颜色越深SR越高。
低频下SR在X轴上呈均匀分布; 随着频率提高, SR出现明显的局域分布, 调节板表面的SR远高于调节板之间覆盖层上的SR, 信号有显著的局域增强。调节板上的SR同样存在着局域分布, 更高的SR主要集中在调节板中央, 随频率提高逐渐向调节板两侧延伸, 与前文分析一致。
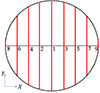 |
图3 Y轴截线及其标号示意图 |
 |
图4 各Y轴截线平均信号比 |
 |
图5 X轴上的信号比空间分布 |
2.3 信号调节板宽度的影响
在小空间中, 声栅的几何尺寸至关重要, 它影响结构的信号增强性能、占用空间和质量。本文研究调节板的宽度L和厚度h对SR的影响, 首先改变调节板的宽度L, 研究SR的分布规律。
沿用2.1节建立的模型, 其余仿真设置不变, 在[0.06, 0.1]m的范围内改变L, 间隔0.005 m, 保持结构仍呈对称分布, 计算调节板上Y轴截线的平均SR。由于篇幅限制, 只展示0.1, 0.08, 0.06 m下的结果以揭示调节板宽度的影响规律。
3种宽度下平均SR的对比结果如图 6所示, 尽管L有所改变, 调节板上方依旧存在显著的局域信号增强。减小L, 中频下的平均SR有所降低, 信号增强的带宽减小, 此外SR出现峰值的频率右移, 捕获模态阶数减少。L为0.08和0.06 m时只出现了第一捕获模态峰值, 但峰值SR有较大提高, 并且高频的信号增强性能更稳定。
上述分析说明: 调节板的宽度越小, 增益峰值越高, 高频信号的增强性能更稳定; 宽度增大, 引起的非镜面散射更强, 局域信号增强的性能越强。增加宽度可以增强中频信号, 提高宽带性能, 增加捕获模态的阶数, 得到更多的SR峰值; 但同时占用的空间和质量也越多, 结构的吸声性能也会有所降低, 影响系统的声隐身性能。因此, 为同时保证多方面实际应用需求, 需要合理地设计信号调节板的宽度。
 |
图6 不同调节板宽度下的平均信号比分布 |
2.4 信号调节板厚度的影响
水下航行器对内部结构的厚度有着严格的限制, 因此研究调节板厚度h对声学性能的影响有重要的现实意义。
沿用2.1节建立的模型, 其余仿真设置不变, 在[0.005, 0.01]m的范围内改变h, 间隔0.000 5 m, 保持结构仍呈对称分布, 计算调节板上Y轴截线的平均SR。由于篇幅限制, 只展示0.01, 0.007 5, 0.005 m下的结果以揭示调节板厚度的影响规律。
3种厚度下的平均SR结果如图 7所示, 对于调节板所在区域来说, h越大, 平均SR越大, 峰值也越大, 中频信号的增益更高。
上述分析说明: 调节板越厚, 同样会引起更强的非镜面散射, 信号增强效果越好, 增强带宽越宽。然而, 受限于航行器内部的小空间, 调节板并不是越厚越好, 在不影响局域信号增强性能的前提下, 选择厚度适宜的信号调节板来设计声栅结构。
 |
图7 不同调节板厚度下的平均信号比分布 |
2.5 声波入射角的影响
以上研究针对的是法向入射的平面波, 对于斜入射平面波, SR的频率及空间分布特性会发生变化。在此研究平面波斜入射对SR的影响, 以确定声波入射角θ是否会限制结构的信号增强性能。
定义入射角为图 1中平面波方向与Z轴的夹角, 沿用2.1节建立的模型, 其余仿真设置不变, 在[0°, 85°]的范围内以5°的间隔改变θ, 计算仿真结果。平面波斜入射情况下模型的声场分布不再对称, 因此分析时对完整模型进行仿真, 计算调节板上Y轴截线的平均SR。同样, 受限于篇幅, 只展示θ=30°下的结果以分析声波斜入射的影响。
调节板中心截线平均SR的频率分布与法向入射情况的比较如图 8所示。“斜入射1”代表斜入射下截线1的平均SR, “法向1”代表法向入射下截线1的平均SR, 后续表示与此类似。
低频下2种情况的平均SR分布一致; 频率在(3.9~15.9)kHz之间时, 斜入射的平均SR略低于法向入射; 在15 kHz以上的高频, 由于入射激励的非对称性, 平均SR表现出与法向入射时调节板1/4处平均SR类似的特征, 如图 9所示。
当平面波斜入射时, 调节板左侧(截线2)的平均SR相较于法向入射时有一定的衰减, 右侧(截线3)反而有所增强, 两截线的平均SR分布不对称, 如图 10所示。在10.4 kHz处, 斜入射情况下的平均SR出现了新的峰值。
为分析原因, 将调节板表面的法向振速与无声栅障板结构的法向振速相减, 取计算结果的对数, 命名为散射表面振速级(scattered surface velocity level, SSL), 计算该频率下信号调节板上方的散射表面振速级分布。如图 11所示, 散射表面振速级分布不对称, 且出现了偶数个波腹, 可以证明10.4 kHz对应于第一反对称捕获模态频率[13]。
在斜入射下, 隔振距离处SR在X轴上的空间分布如图 12所示, SR分布不对称, 调节板右侧的SR大于左侧, 但仍然有着显著的局域信号增强。
 |
图8 截线1的法向、斜入射平均SR对比 |
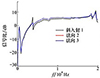 |
图9 斜入射(截线1)与法向入射(截线2, 3)平均SR对比 |
 |
图10 截线2, 3的法向、斜入射平均SR对比 |
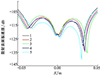 |
图11 10.4 kHz处散射表面振速级分布 |
 |
图12 X轴上的SR空间分布 |
3 多周期声栅结构声学性能及其影响因素
对于反声障板上方的水听器阵列来说, 其周期性分布特性可以与声栅的周期性局域增强特性达成良好匹配。因此, 在单周期声栅结构的研究基础上, 在有限尺寸的圆形覆盖层障板上设计多周期声栅结构是一个合理的选择。本节通过仿真研究其声学性能及影响因素。
3.1 多周期声栅结构声学性能仿真
假设某水下航行器在反声障板上方安装了4列水听器(每列的个数根据实际情况决定, 不影响本文研究), 如图 13所示。
因此在单周期声栅模型的基础上, 在其上方敷设4块调节板得到多周期声栅模型(1/4模型如图 14所示)。具体计算时, 设置圆盘半径为0.5 m, 调节板间隔0.02 m, 关于Y轴对称分布。
与单周期声栅结构的研究方法一致, 分析SR在结构宽度方向上的空间分布特征, 计算隔振距离为0.007 5 m时X轴上的SR分布, 结果如图 15所示。
图 15显示, 多周期声栅结构能够在局部空间周期性地增强入射信号, SR具有明显的局域分布特征: 4个调节板上方均存在显著的信号增强。与单周期声栅不同, 四周期声栅SR关于中心呈偶对称分布, 同一频率下单个调节板表面的SR分布并不对称, 但不同位置的信号增强性能无明显差异, 信号不存在显著衰减。
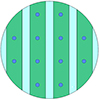 |
图13 某航行器反声障板上方的4列水听器 |
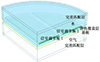 |
图14 多周期声栅结构仿真模型 |
 |
图15 X轴上的SR空间分布 |
3.2 影响多周期声栅结构声学性能的各种因素
多周期声栅上敷设了多个信号调节板, 因此一个周期的长度l为结构重要的几何参数, 设为调节板宽度L与两调节板间隔d之和。
2.3节的分析说明, L越大, 信号综合增强性能越好。但是在尺寸确定的有限空间内, 无法简单拓宽l。因此, 在l不变的情况下, 分析L与d的比值(宽度比)对结构声学性能的影响。固定l=0.12 m, 建立3种多周期声栅模型:①L=0.1 m, d=0.02 m(L/d=5);②L=0.08 m, d=0.04 m(L/d=2);③L=0.06 m, d=0.06 m(L/d=1)。
在调节板中心及1/4处设置Y轴截线, 对比3种宽度比下SR的频率分布特性, 由于不同声栅上的分布近似, 只展示声栅1上的平均SR分布, 如图 16所示。
对于调节板表面而言, L/d越大, 中频信号的增强效果越好; 平均SR的峰值频率左移, 对应峰值降低。L/d减小时, 第一捕获模态频率下的增益峰值显著提高。在高频下, 不同L/d下的平均SR性能基本相当。
3种L/d下X轴上SR的空间分布如图 17所示。尽管L/d不同, 但声栅的周期性局域信号增强特征依旧显著。L/d越大, 中频下调节板上的SR明显提高, 信号增强带宽显著增加。而L/d越小, SR的峰值更高。
高宽度比会提高信号的增强性能, 而低宽度比会显著提高信号增益的峰值, 为兼顾多个声学性能, 同时考虑质量以及空间的应用要求, 需要选择合适的宽度比。
 |
图16 不同Y轴截线下的SR空间分布 |
 |
图17 不同宽度比下X轴上的SR空间频率分布 |
4 结论
本文对小空间中单周期和多周期的声栅结构进行了建模, 对其声学性能和影响因素进行了仿真分析。通过对结构宽度方向上频率、空间的性能分析, 证明声栅能够精准地在声栅上方增强入射信号。分析了入射角度对性能的影响, 结果表明, 声波的斜入射改变了SR的对称分布, 激发了结构的反对称捕获模态, 但并未大幅改变结构的声学性能。对信号调节板宽度、厚度的分析说明: 调节板越宽、越厚, 其综合信号增强性能就越好, 对(2~10)kHz的中频信号增强效果越高。但是, 受到实际应用中小空间的限制, 只能合理地设计几何参数以达到平衡。多周期声栅结构的性能分析反映了显著的周期性局域信号增强性能, 对结构宽度比的研究证明, 选择适中的宽度比能使结构获得良好的综合声学性能。在研究各个参数对声栅结构信号增强性能的影响时,存在多个参数的交叉影响,因而声栅结构信号增强性能的变化可能是非线性的,甚至更加复杂。受限于篇幅, 本文的研究主要从工程应用的角度, 使用简单的控制变量法研究各个因素对声栅结构信号增强性能的影响, 从而指导在工程中选择最合适的声栅结构参数。在后续关于信号增强机理与优化设计的研究中会进一步考虑。
References
- KO S H, PYO S, SEONG W. Structure-borne and flow noise reductions(mathematical modeling)[M]. Korea: Seoul National University Press, 2001: 34–98 [Google Scholar]
- SHERMAN C, BUTLER J. Transducers and arrays for underwater sound[M]. New York: Springer, 2007: 289–291 [Google Scholar]
- ZHANG Yijun. The study of cylindrical array layout technology[D]. Harbin: Harbin Engineering University, 2017: 46–47 (in Chinese) [Google Scholar]
- BIAN Hanlin, XIA Tiejian. The study of a cylindrical channel type rubber acoustic baffle[J]. Acoustics and Electronics Engineering, 2014(1): 31–33 [Article] (in Chinese) [Google Scholar]
- ZHANG Y, PAN J. Underwater sound scattering and absorption by a coated infinite plate with a distributed inhomogeneity[J]. Journal of the Acoustical Society of America, 2013(133): 2082–2096 [NASA ADS] [CrossRef] [Google Scholar]
- ZHANG Y, PAN J. Enhancing acoustic signal response and absorption of an underwater coated plate by embedding periodical inhomogeneities[J]. Journal of the Acoustical Society of America, 2017, 142(6): 3722–3735 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- FEIT D, CUSCHIERI J M. Scattering of sound by a fluid-loaded plate with a distributed mass inhomogeneity[J]. Journal of the Acoustical Society of America, 1996, 99(5): 2686–2700 [Article] [CrossRef] [Google Scholar]
- CUSCHIERI J M, FEIT D. Full numerical solution for the far-field and near-field scattering from a fluid-loaded elastic plate with distributed mass or stiffness inhomogeneity[J]. Journal of the Acoustical Society of America, 1998, 104(2): 915–925 [Article] [CrossRef] [Google Scholar]
- SMITH S G, CRASTER R V. Numerical and asymptotic approaches to scattering problems involving finite elastic plates in structural acoustics[J]. Wave Motion, 1999(30): 17–41 [CrossRef] [Google Scholar]
- GUO Y P. Effects of structural joints on sound scattering[J]. Journal of the Acoustical Society of America, 1993(93): 857–863 [CrossRef] [Google Scholar]
- WANG Haijun, GUO Xinglin. The study of coincidence frequency and critical frequency characteristics of plate structures[C]//Proceedings of the 17th National Conference on Structural Engineering, 2008: 570–575 [Google Scholar]
- POSTNOVA J, CRASTER R V. Trapped modes in topographically varying elastic waveguides[J]. Wave Motion, 2007, 44(3): 205–221 [Article] [CrossRef] [Google Scholar]
- ZHANG Y, PAN J. Underwater sound radiation from an elastically coated plate with a discontinuity introduced by a signal conditioning plate[J]. Journal of the Acoustical Society of America, 2013(133): 173–185 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
图1 周期性声栅复合结构 |
| In the text | |
 |
图2 单周期声栅结构仿真模型 |
| In the text | |
 |
图3 Y轴截线及其标号示意图 |
| In the text | |
 |
图4 各Y轴截线平均信号比 |
| In the text | |
 |
图5 X轴上的信号比空间分布 |
| In the text | |
 |
图6 不同调节板宽度下的平均信号比分布 |
| In the text | |
 |
图7 不同调节板厚度下的平均信号比分布 |
| In the text | |
 |
图8 截线1的法向、斜入射平均SR对比 |
| In the text | |
 |
图9 斜入射(截线1)与法向入射(截线2, 3)平均SR对比 |
| In the text | |
 |
图10 截线2, 3的法向、斜入射平均SR对比 |
| In the text | |
 |
图11 10.4 kHz处散射表面振速级分布 |
| In the text | |
 |
图12 X轴上的SR空间分布 |
| In the text | |
 |
图13 某航行器反声障板上方的4列水听器 |
| In the text | |
 |
图14 多周期声栅结构仿真模型 |
| In the text | |
 |
图15 X轴上的SR空间分布 |
| In the text | |
 |
图16 不同Y轴截线下的SR空间分布 |
| In the text | |
 |
图17 不同宽度比下X轴上的SR空间频率分布 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


