| Issue |
JNWPU
Volume 42, Number 5, October 2024
|
|
|---|---|---|
| Page(s) | 847 - 856 | |
| DOI | https://doi.org/10.1051/jnwpu/20244250847 | |
| Published online | 06 December 2024 | |
Multi-objective performance optimization of turbofan engine for test run
面向检验试车的涡扇发动机多目标性能优化
1
AECC Aviation Power Co., Ltd, Xi’an 710021, China
2
School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China
Received:
2
September
2023
Turbofan engines are widely used in military and civilian aviation fields due to their high propulsion efficiency and low fuel consumption rate, and their performance directly affects the safety and stability of flight mission. It is of great practical significance to optimize the turbine inlet temperature and high-pressure compressor speed under different thrust states, so as to improve the pass rate of the first test run. This paper proposes a multi-objective performance optimization framework for turbofan engines. On the historical production dataset of a certain type of turbofan engine, the turbine inlet temperature and high-pressure compressor speed under different thrusts are taken as target variables, and area variable a, area variable b, and angle variable c in the assembly stage are taken as attribute variables. Then, the multi-objective performance optimization model based on tree augmented naive bayes is established and compared and verified with the current mainstream algorithm for verification. Finally, combining with the posterior qualified probability inference and state combination global search method, a recommended state combination table is given to assist enterprises in the formulation of component production and manufacturing assembly standards, thereby optimizing turbofan engine performance, reducing reassembly requirements, and improving the pass rate of the first test run.
摘要
涡扇发动机因其高推进效率、低燃油消耗率等特点广泛应用于军民用飞机, 其性能直接影响飞行任务的安全与稳定。针对涡扇发动机不同状态下涡轮前温度与高压转速比指标进行性能优化, 从而提高其一次检验试车通过率, 具有重要现实意义。提出涡扇发动机的多目标性能优化框架, 在某型号涡扇发动机历史生产数据集上, 以检验试车过程中不同状态下涡轮前温度与高压转速比为目标变量, 以某面积a、某面积b、某角度c为属性变量, 建立涡扇发动机多目标性能模型并与目前主流算法模型对比验证, 最后结合通过检验试车的后验概率推理与状态组合全局搜索, 给出推荐状态组合表, 辅助企业制定零部件生产制造装配标准, 从而优化涡扇发动机性能、减少重新装配次数并提高一次检验试车通过率。
Key words: tree augmented naive Bayes / performance optimization framework / turbofan engine / multi-objective performance optimization
关键字 : 树增强贝叶斯网络 / 性能优化框架 / 涡扇发动机 / 多目标性能优化
© 2024 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
航空发动机是一种高度复杂和精密的热力机械系统, 被誉为“现代工业皇冠上的明珠”[1]。涡扇发动机因其高推进效率、低燃油消耗率等特点, 广泛应用于军用、民用航空领域, 在国防建设与国民经济中具有极其重要的地位[2–3]。
为保证在各飞行条件下均能安全稳定运行, 涡扇发动机新机出厂前需要进行检验试车并严格考查各项性能指标以综合评判其性能状态。目前我国涡扇发动机部分新机出厂前即使各项装配参数均满足装配要求, 但仍会因性能问题需要多次装配才能通过检验试车, 这大大增加了涡扇发动机的生产周期与生产成本。不同状态下涡轮前温度与高压转速比是涡扇发动机检验试车中常见的性能指标, 过高可能会导致关键部件损坏,寿命降低,甚至引发重大安全事故。产品设计中性能已做的优化最终体现在按照产品设计给出的装配参数要求上, 但装配参数数量繁多, 其中部分是承袭上一代发动机的装配参数要求, 装配参数区间较为宽泛, 尤其是在新型号发动机生产之初。而检验试车过程中, 客户要求新出厂的发动机需要在特定状态下满足特定性能要求, 企业在实际生产过程中对于某些装配参数通常会实行更严格的装配要求。因此, 企业在实际生产制造过程中不仅需要考虑设计过程中规定的装配要求, 还需要在此基础上进一步满足客户验收所规定的性能要求。综上所述, 为保证涡扇发动机使用安全与使用寿命, 在其装配要求范围内, 针对涡扇发动机不同状态下涡轮前温度与高压转速比指标进行性能优化, 从而提高其一次检验试车通过率, 具有重要现实意义。
近年来, 随着发动机历史数据积累与人工智能的高速发展, 许多学者利用人工智能算法探索提升发动机性能的可能性。陈果[4]建立基于遗传算法的结构自适应神经网络预测模型, 并使用民航发动机性能数据证明了模型的有效性。Kiakojoori等[5]采用动态神经网络方法, 根据零部件退化数据进行发动机的性能预测与优化, 为航空发动机的性能管理提供了新的视角和思路。基于融合长短时记忆网络与深度置信网络, 李京峰等[6]提出一种剩余寿命预测方法并在商用航空发动机数据集上验证该方法的可行性。Zhang等[7]提出一种基于熵损失函数的极限学习机算法, 针对易受噪声和异常值影响的复杂航空发动机进行剩余寿命预测。周涛等[8]等提出一种数模联动随机退化设备剩余寿命预测方法, 并在涡扇发动机运行数据集上进行验证。林志富等[9]构建内嵌物理约束的神经网络架构并建立航空发动机的推力预估数字模型进行航空发动机性能参数预估。
作为人工智能领域重要研究方向之一, 贝叶斯网络被视为复杂系统不确定性推理与数据分析的一种有效工具[10], 并广泛应用于医疗诊断、文本识别、可靠性分析等各个领域[11–15]。本文将树增强贝叶斯网络引入涡扇发动机的多目标性能优化中, 提出涡扇发动机的多目标性能优化框架, 在某型号涡扇发动机数百台检验试车数据基础上, 以不同状态下涡轮前温度与高压转速比为目标变量, 以装配阶段某面积a、某面积b、某角度c为属性变量, 建立涡扇发动机多目标性能模型, 最后结合后验概率计算与全局搜索给出推荐状态组合表, 实现涡扇航空发动机性能优化并提高其一次检验试车通过率。
1 涡扇发动机的多目标性能优化框架
1.1 涡扇发动机的性能优化目标
涡扇发动机因其高推进效率、低燃油消耗率等特点广泛应用于军民航空应用领域。在新机出厂前, 需要通过试车检验涡扇发动机能否在各飞行条件下均安全稳定运行, 其中不同状态下涡轮前温度与高压转速比是极其重要的性能指标。然而, 在企业实际生产过程中, 即使各项装配参数均满足装配要求, 涡轮前温度与高压转速比往往不能降低至最高限制值以下, 导致需要多次重新装配并重新进行检验试车, 这无形中增加了企业额外的生产成本与生产周期。
通过企业调研与技术人员讨论, 我们发现改变涡扇发动机装配过程中某面积a、某面积b、某角度c会对中间状态下涡轮前温度(M)、高压转速比(N)与最大连续状态下涡轮前温度(P)、高压转速比(Q)造成显著影响。具体地, 通过调整某面积a、某面积b、某角度c可对进入涡扇发动机的空气流造成影响, 各参数大致位置结构可参考图 1。因此, 本文的优化目标是: 在装配要求范围内, 找到装配阶段某面积a、某面积b、某角度c的区间及其组合方式, 尽可能提高上述4个性能指标同时通过涡扇发动机检验试车要求的概率。
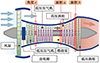 |
图1 某面积a、某面积b、某角度c结构位置图 |
1.2 涡扇发动机的多目标性能优化框架
常用的多目标优化方法, 如Pareto优化方法[16–17]等往往不能显式表达目标,针对实际工程问题求解难度较大。在本文所研究的涡扇发动机多目标性能优化问题中, 需要综合考虑多个性能参数目标变量且其无显式的目标函数, 即需要判断一台待预测涡扇发动机不同状态下涡轮前温度与高压转速比是否能够满足各自的合格条件, 这本质上属于机器学习中的分类预测问题。因此, 以贝叶斯网络为首的机器学习算法中的分类预测算法更适合解决此类问题, 更适用于处理实际工程问题。
在常规的机器学习算法中, 通过训练得到符合要求的算法模型, 对于一个新样本, 根据上述模型得到该样本所属类别的预测结果, 从而辅助决策。但在实际企业运营过程中, 当一台发动机装配完成, 借助上述算法模型, 可以得到该台发动机能否通过检验试车的预测结果, 如果结果为否, 则需要重新装配并再次预测, 直至通过检测。在此种模式下, 多次装配的存在导致上述算法模型仅起到预测结果作用且并不能有效地为企业减少实际生产成本。在实际生产制造过程中, 相比于预测能否通过检验试车, 企业更想得知如何生产装配才能使发动机通过检验试车。
基于该实际问题, 本文设计一种涡扇发动机的多目标性能优化框架。在数据处理后, 该优化框架首先针对所有目标变量分别建立单目标树增强贝叶斯网络模型, 接着对所有单目标模型进行状态组合搜索, 并通过后验概率的计算、排序、筛选得到各个目标变量的属性变量状态组合情况, 得到多目标性能模型, 最后综合多目标性能要求, 得到同时使所有目标变量后验概率最大属性变量状态组合,以此作为最后解集。上述优化框架如图 2所示。该优化框架也可被应用至其他相关领域解决实际优化问题。
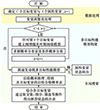 |
图2 涡扇发动机的多目标性能优化框架 |
1.3 数据准备
本文提取含有1.1节中7个变量的数百条某型号涡扇发动机检验试车数据, 其中M, N, P, Q为目标变量, a, b, c为属性变量。本文使用涡扇发动机数据一般描述如表 1所示。本文所使用数百条某型号涡扇发动机检验试车数据各项装配参数均符合装配要求。在此基础上, 使用随机分割方法将其80%作为训练集, 20%作为测试集用于后续评价模型。
由于树增强贝叶斯网络属于分类预测模型的一种, 算法要求输入的变量必须是离散变量。针对目标变量M, N, P, Q, 按照检验试车通过标准将其分为2段。具体地, 符合检验试车通过标准为1, 不符合为2。针对属性变量, 首先采用肘部法则确定各属性变量的合理聚类数目, 再通过KMEANS算法进行聚类。属性变量a, b, c由肘部法则得到的聚类数对比如图 3所示, 该图用于选择较好的聚类数量, 通过“坡度趋于平缓”找出各属性变量的最佳类簇数量, 决定将其均离散化为4类。接着, 利用KMEANS算法对已有的属性变量数据进行聚类, 从而划分区间, 并对每一区间给定一个数字编码。目标变量与属性变量的离散化结果见表 2。
数据一般描述
 |
图3 属性变量a, b, c的聚类数对比图 |
变量离散化结果
2 涡扇发动机多目标性能模型
2.1 树增强贝叶斯网络
作为贝叶斯方法与图论的有机结合, 贝叶斯网络在各领域具有广泛的应用[18]。在该模型中, 随机变量用节点的形式体现, 变量之间的依赖关系用节点之间有向边的形式体现, 见图 4a)。
然而, 贝叶斯网络的条件独立假设在现实研究与应用中往往不成立, 其原因是某些节点间的关联往往是十分必要的。树增强贝叶斯网络针对这一现实要求, 在贝叶斯网络的基础上, 通过在部分节点间添加必要的边建立树结构, 放宽了其条件独立假设[19]。如图 4b)所示, 在树增强贝叶斯网络中, 属性变量Xi的父节点不仅包括目标节点C, 还可能同时包括其他节点, 其中属性变量间的关联关系用黑色箭头表示。
式中:Xi为属性变量;Pa(Xi)为节点Xi的父节点。
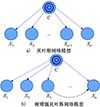 |
图4 贝叶斯网络与树增强贝叶斯网络 |
2.2 模型构建
在数据离散化的基础上, 分别针对中间状态下涡轮前温度(M)、高压转速比(N)与最大连续状态下涡轮前温度(P)、高压转速比(Q)这4个目标变量建立4个树增强贝叶斯网络模型, 最终构成涡扇发动机多目标性能模型, 见图 5。该模型旨在计算属性变量各区间组合的后验概率并找出目标变量后验概率较大的属性变量状态组合作为最后解集。
其中, 以中间状态下涡轮前温度(M)这一目标变量为例, 基于树增强贝叶斯网络建立了M的性能模型网络结构, 如图 5a)所示。在该模型中, 目标变量M为父节点, 其余变量为子节点。通过模型, 可以计算得到目标变量的概率分布表及各属性变量的条件概率表, 以此来将各变量间的依赖关系通过概率量化, 具体见表 3~4。
在建立了一个完整的树增强贝叶斯网络模型之后, 下一步需要列出所有可能的属性变量状态组合。在上述模型中有3个属性变量a, b, c, 每个属性变量又分为4种状态(1, 2, 3, 4), 因此可能的状态组合总共有64种。然后, 将这些状态组合依次输入到模型中, 通过概率推理进行后验概率计算, 得到目标变量的后验概率表, 我们将在下一章节展开。
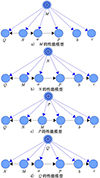 |
图5 涡扇发动机多目标性能模型 |
目标变量M, N, P, Q的概率分布表
属性变量的条件概率表 %
2.3 模型对比验证
在正式使用涡扇发动机多目标性能模型进行性能优化分析前, 需要进行评估。模型准确率是通过将测试集数据输入模型, 比较目标变量的预测值与实际值计算得到, 同时可画出对应的受试者工作特征曲线(ROC曲线), 该曲线下方面积越大则预测准确率越高。通过计算, 本文建立的涡扇发动机多目标性能模型准确率为95.76%, 模型受试者工作特征曲线(ROC曲线)下面积为92.17%, 见图 6。
为体现树增强贝叶斯网络中树结构的优越性, 使用朴素贝叶斯网络进行建模用以对比, 得到基于朴素贝叶斯网络模型准确率为92.42%, 模型受试者工作特征曲线(ROC曲线)下面积仅为77.63%, 见图 7。这说明在实际生产制造过程中, 考虑某些节点间的关联是必要且更贴合实际的。
此外, 将本文建立的涡扇发动机多目标性能模型在同一测试集上使用交叉验证方法与常见的机器学习算法模型进行对比, 包括朴素贝叶斯网络(NB)[20]、线性判别分析模型(LDA)[21]、决策树模型(DT)[22]、逻辑回归模型(LR)[23]、马尔科夫毯模型(MB)[24]和半导师学习模型(MT)[25]。
此处采用了5个常用的性能评价指标[21]用以评价模型, 包括准确率、F1值、精确率、特异度和召回率。通过构建五维雷达图并将5个性能指标计算值绘在图中, 以直观比较各模型的综合性能。在图 8所示的各模型性能表现可视化雷达图中, 代表模型的图形所占面积越大, 则其综合性能越好。由图 8可得, 红线代表本文构建的模型, 其所占面积最大, 各项指标较好, 综合性能更佳。
综上所述, 本文所构建的涡扇发动机多目标性能模型具有较高的准确率。通过与其他常用模型的对比可知, 本文模型综合性能更优, 在此基础上的优化分析也更具可信度。
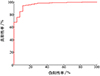 |
图6 本文所构建模型的ROC曲线 |
 |
图7 基于朴素贝叶斯网络模型的ROC曲线 |
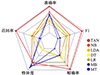 |
图8 各模型的性能表现雷达图 |
3 涡扇发动机多目标性能优化策略
在完成涡扇发动机多目标性能优化模型的构建与对比验证后, 通过对所有属性变量状态组合的全局搜索给出优化方案。首先将共计64种属性变量a, b, c的状态组合输入模型, 通过后验概率推理, 分别得到使各目标变量符合检验试车要求的后验概率表。最后, 针对所有状态组合, 综合所有目标变量要求, 通过取交、筛选、排序得到推荐状态组合表, 并通过与技术人员讨论从发动机工作原理的角度给出解释, 指导企业实际生产。
3.1 模型后验概率计算
针对目标变量为M的涡扇发动机性能模型, 将64种属性变量状态组合输入性能模型进行后验概率推理计算, 并将其降序排列, 得到表 5结果。由于篇幅有限, 仅节选前10个与最后10个状态组合。
以表 5第一种情况为例, 计算目标变量M通过检验试车的后验概率。根据贝叶斯公式, 当M=1时有
根据图 4可对(2)式进一步化简
式中, 分子中P(M=1)可通过查询表 3得到,为91.52%, P(a=4|M=1)等3个属性变量的条件概率值可通过查询表 4得到, 分别为24.50%, 13.91%和16.89%, 同时将分母固定, 得
同理, 当M=2时, 有
由概率论知识, (4)~(5)式和为1, 解得D为0.005 25, 并将其代入(3)式可得
至此, 便可得到: a, b和c的状态组合为[4, 1, 1]时, 目标变量M通过检验试车的后验概率为100%。
在表 5所示的模型后验概率表中, 若企业在检验试车过程中采用处于越高位置状态组合, 则中间状态下涡轮前温度(M)小于等于1y30 K的概率越高, 反之则概率越低。以表 5中第一个状态组合[4, 1, 1]为例, 若面积a的装配尺寸落在4区间, 即[0.026 761 9, 0.027 046 4], 面积b和角度c分别落在其对应的1区间, 中间状态下涡轮前温度小于等于1y30 K的概率最大, 理论上概率为100%;以表 5中最后一个状态组合为例, 若[a, b, c]为[1, 4, 4], 则涡轮前温度小于等于1y30 K的概率仅有22.33%, 这也是企业在实际生产装配过程中最不应该出现的属性状态组合。
类似地, 分别给出目标变量为N, P和Q的模型后验概率表, 见表 6~8。
目标变量M的模型通过检验试车的后验概率表
目标变量N的模型通过检验试车的后验概率表
目标变量P的模型通过检验试车的后验概率表
目标变量Q的模型后验概率表
3.2 涡扇发动机多目标性能优化方案
综合考虑中间状态和最大连续状态2种情况下对涡轮前温度与高压转速比的要求, 对所有属性变量的状态组合及其对应各目标变量的后验概率进行计算、筛选、取交并排序, 综合给出如表 9所示的推荐状态组合表, 其中P为所有目标性能均通过检验试车的概率, 建议实际生产中可采用表 9的状态组合。
对于上述推荐状态组合表, 可以看出面积a和面积b更倾向于取面积较小的1和2区间, 通过与企业一线技术人员讨论, 其原理为同时使面积a和面积b取较小状态, 令高压涡轮状态不变的同时使得低压涡轮落压比增加, 提高低压转速比, 因此在相同状态下涡轮前温度与高压转速比降低, 更可能通过检验试车。
通过对所有属性变量的状态组合进行全局搜索, 得到可指导实际生产装配的优化方案与推荐状态组合表, 且该结果从发动机工作原理上具有可解释性。在后续企业实际生产过程中, 可适当综合考虑成本, 尽可能选择在推荐状态组合表中靠前的状态组合。
推荐状态组合表
4 结论
本文主要研究多目标下涡扇发动机的性能优化策略。针对企业不能同时保证在中间状态与最大连续状态下涡轮前温度与高压转速比达到较低要求这一实际问题, 首先提出涡扇发动机的多目标性能优化框架, 接着在某型号涡扇发动机数百台检验试车数据基础上建立涡扇发动机多目标性能模型;通过与朴素贝叶斯网络、线性判别分析模型、决策树模型、逻辑回归模型、马尔科夫毯模型和半导师学习模型对比分析, 证明本文所提出的模型综合性能更优且更贴合实际;最后将属性变量的64种状态组合输入模型计算通过检验试车的后验概率, 综合4个目标变量进行全局搜索要求给出涡扇发动机多目标性能优化方案与推荐状态组合表, 用以指导涡扇发动机实际生产活动, 实现涡扇航空发动机多目标性能优化并提高其一次检验试车通过率。
References
- JIAO Huabin, MO Song. Present status and development trend of aircraft turbine engine[J]. Aeronautical Manufacturing Technology, 2015, 58(12): 62–65 (in Chinese) [Google Scholar]
- GARG S. NASA glenn research in controls and diagnostics for intelligent aerospace propulsion systems[R]. NASA TM-2005-214036, 2005 [Google Scholar]
- SUN Jianguo. Modern aviation power plant control[M]. Beijing: Aviation Industry Press, 2009 (in Chinese) [Google Scholar]
- CHEN Guo. Forecasting engine performance trend by using structure self-adaptive neural network[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(3): 535–539 [Article] (in Chinese) [Google Scholar]
- KIAKOJOORI S, KHORASANI K. Dynamic neural networks for gas turbine engine degradation prediction, health monitoring and prognosis[J]. Neural Computing and Applications, 2016, 27(8): 2157–2192 [Article] [CrossRef] [Google Scholar]
- LI Jingfeng, CHEN Yunxiang, XIANG Huachun, et al.. Remaining useful life prediction for aircraft engine based on LSTM-DBN[J]. Systems Engineering and Electronics, 2020, 42(7): 1637–1644 (in Chinese) [Google Scholar]
- ZHANG B, LI Y, BAI Y, et al.. Aeroengines remaining useful life prediction based on improved C-loss ELM[J]. IEEE Access, 2020, 8:49752–49764 [Article] [NASA ADS] [CrossRef] [Google Scholar]
- ZHOU Tao, WANG Yongchao, ZHANG Xujing, et al.. Data-model interactive remaining useful life prediction of stochastic degrading devices based on deep feature fusion network[J]. Computer Integrated Manufacturing Systems, 2022, 28(12): 3937–3945 (in Chinese) [Google Scholar]
- LIN Zhifu, XIAO Hong, WANG Zhanxue, et al.. An aeroengine digital engineering model based on physics-embedded neural networks[J]. Journal of Propulsion Technology, 2023, 44(11): 54–65 (in Chinese) [Google Scholar]
- CHEN Yingwu, GAO Yanfang. Survey of extended Bayesian networks[J]. Control and Decision, 2008, 23(10): 1081–1086 [Article] (in Chinese) [Google Scholar]
- CAI Z, GUO P, SI S, et al.. Analysis of prognostic factors for survival after surgery for gallbladder cancer based on a Bayesian network[J]. Scientific Reports, 2017, 7(1): 293 [Article] [CrossRef] [Google Scholar]
- PETOUSIS P, HAN S X, ABERLE D, et al.. Prediction of lung cancer incidence on the low-dose computed tomography arm of the national lung screening trial: a dynamic Bayesian network, Artificial Intelligence in Medicine, 2016, 72: 42–55 [Article] [CrossRef] [Google Scholar]
- ZHENG Wei, SHEN Wen, ZHANG Yingpeng. Implement spam filter by improving naïve Bayesian algorithm[J]. Journal of Northwestern Polytechnical University, 2010, 28(4): 622–627 [Article] (in Chinese) [Google Scholar]
- LI Naixin, LU Zhong, ZHOU Jia. Reliability assessment based on Bayesian networks for electro hydraulic servo actuator[J]. Journal of Northwestern Polytechnical University, 2016, 34(5): 915–920 [Article] (in Chinese) [Google Scholar]
- WANG Ning, WANG Yuhang, CAI Zhiqianget al.. Performance optimization scheme of turboshaft aeroengine based on Bayesian network[J]. Journal of Northwestern Polytechnical University, 2021, 39(2): 375–381 [Article] [CrossRef] [EDP Sciences] [Google Scholar]
- HOU Yan, HUANG Kanghuan, ZHANG Yixian, et al.. A multi-objective scheduling optimization for crude oil operations[J]. Industrial Engineering Journal, 2020, 23(4): 131–139 (in Chinese) [Google Scholar]
- TU Nan, CHANG Liufeng, MEHRBOD Mehrdad, et al.. Multi-objective optimization of closed-loop logistics network with facility expansion[J]. Industrial Engineering Journal, 2013, 16(5): 53–61 (in Chinese) [Google Scholar]
- ZHANG Lianwen, GUO Haipeng. Introduction to Bayesian networks[M]. Beijing: Science Press, 2006 (in Chinese) [Google Scholar]
- FRIEDMAN N, GEIGER D, GOLDSZMIDT M. Bayesian network classifiers[J]. Machine Learning, 1997, 29(2/3): 131–163 [Article] [CrossRef] [Google Scholar]
- MUGHAL M, KIM S. Signal classification and jamming detection in wide-band radios using naive Bayes classifier[J]. IEEE Communications Letters, 2018, 22(7): 1398–1401 [Article] [CrossRef] [Google Scholar]
- ZHOU Zhihua. Machine Learning[M]. Beijing: Tsinghua University Press, 2016: 1–18 (in Chinese) [Google Scholar]
- LEE V, LYE D, SUN Y, et al.. Decision tree algorithm in deciding hospitalization for adult patients with dengue haemorrhagic fever in Singapore[J]. Tropical Medicine & International Health, 2010, 14(9): 1154–1159 [Google Scholar]
- WU Y, YANG H, ZHANG L, et al.. Application of crossover analysis-logistic regression in the assessment of gene-environmental interactions for colorectal cancer[J]. Asian Pacific Journal of Cancer Prevention, 2012, 13(5): 2031–2037 [Article] [Google Scholar]
- LING Z L, YU K, ZHANG Y W, et al.. Causal learner: a toolbox for causal structure and Markov blanket learning[J]. Pattern Recognition Letters, 2022, 163(2): 92–95 [CrossRef] [Google Scholar]
- TARVAINEN A, VALPOLa H. Mean teachers are better role models: weight-averaged consistency targets improve semi-supervised deep learning results[C]//31th Conference on Neural Information Processing System, Long Beach, USA, 2017 [Google Scholar]
All Tables
All Figures
 |
图1 某面积a、某面积b、某角度c结构位置图 |
| In the text | |
 |
图2 涡扇发动机的多目标性能优化框架 |
| In the text | |
 |
图3 属性变量a, b, c的聚类数对比图 |
| In the text | |
 |
图4 贝叶斯网络与树增强贝叶斯网络 |
| In the text | |
 |
图5 涡扇发动机多目标性能模型 |
| In the text | |
 |
图6 本文所构建模型的ROC曲线 |
| In the text | |
 |
图7 基于朴素贝叶斯网络模型的ROC曲线 |
| In the text | |
 |
图8 各模型的性能表现雷达图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


