Task allocation and path planning for multi-robot systems in intelligent warehousing

Jing CHU; Yiqiu TIAN; Qi YUE; Yong HUANG

doi:10.1051/jnwpu/20244250929

All issues

Volume 42 / No 5 (October 2024)

JNWPU, 42 5 (2024) 929-938

Full HTML

Open Access

Issue		JNWPU Volume 42, Number 5, October 2024


Page(s)		929 - 938
DOI		https://doi.org/10.1051/jnwpu/20244250929
Published online		06 December 2024

JNWPU 2024, 42(5): 929–938

Task allocation and path planning for multi-robot systems in intelligent warehousing

面向智能仓储的多机器人任务分配及路径规划

Jing CHU (褚晶)¹, Yiqiu TIAN (田艺秋)¹, Qi YUE (岳颀)¹ and Yong HUANG (黄勇)²

¹ School of Automation, Xi'an University of Posts and Telecommunications, Xi'an 710121, China
² School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China

Received: 1 December 2023

Abstract

Faced with today's increasingly complex market demands, traditional manual warehouse systems are becoming inadequate, necessitating the urgent intelligent transformation and upgrading of warehouse systems. In this context, this paper aims to design a task allocation and path planning strategy for a multi-robot warehouse system to efficiently accomplish mixed single-robot and multi-robot types of warehouse tasks. The study proposes a warehouse task allocation strategy that incorporates traffic flow impact factors into the auction algorithm, optimizing task allocation by predicting robot density in various areas of the environment. For multi-robot formation tasks, a three-robot formation model based on the virtual structure method is designed. Additionally, a two-layer path planning strategy is proposed: the outer layer conducts global path planning based on the Floyd algorithm, while the inner layer resolves various collision issues through traffic rule constraints, achieving local optimal path planning. Simulation experiments conducted on the MATLAB platform show that the multi-robot system can flexibly handle mixed types of warehouse tasks, effectively reducing collision risks between robots and stagnation in dense areas, thereby improving the safety and efficiency of the multi-robot system. This study provides a reference for future research and practical applications of multi-robot systems.

摘要

面对当今日益复杂的市场需求, 传统的人工仓储系统已力不从心, 仓储系统的智能化转型升级成为迫切需求。在这一背景下, 针对仓储环境设计了一种仓储多机器人系统的任务分配与路径规划策略, 以实现混杂单机与多机编队仓储任务的高效完成。文中提出一种将交通流量影响因子融入拍卖算法的仓储任务分配策略, 通过预测环境中各区域机器人密度, 实现任务分配的优化。该研究为多机编队任务设计了基于虚拟结构法的三机器人编队模型, 并提出一种2层路径规划策略: 外层基于Floyd算法进行全局路径规划, 内层通过交通规则约束解决各类碰撞问题, 实现局部路径规划。在MATLAB平台对设计的仓储多机器人系统进行仿真实验, 实验结果表明, 该多机器人系统能够灵活处理混杂2种类型的仓储任务, 有效减少机器人之间的碰撞风险和机器人在密集区域的停滞现象, 从而提高系统的安全性和工作效率。该研究为未来多机器人系统研究和现实应用提供参考。

Key words: warehousing system / multi-robot system / task allocation / path planning / multi-robot collaboration

关键字 : 仓储系统 / 多机器人系统 / 任务分配 / 路径规划 / 多机器人协同

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

在现代仓储物流行业中，自动化和智能化已成为提高效率和降低成本的关键途径。机器人系统(multi-robot systems, MRS)因其高灵活性和高效率，广泛应用于仓储物流领域。然而仓储环境具有通道狭窄、障碍物多、存在动态变化等特点，需完成的仓储任务具有数量多、多样化等特点，其中任务多样性主要表现在货物的取货地点、送货地点以及尺寸大小各不相同。如何在复杂的仓储环境中实现多机器人协同工作，避免碰撞，优化任务分配和路径规划，仍是一个具有挑战性的研究课题。

目前大多文献在为多机器人任务分配时未充分考虑仓储任务的多样性。单个机器人无法完成较大货物的搬运工作，为完成该任务，可以选用多机器人协同编队的方法[1]。基于此，本研究将针对混杂单机器人与多机器人仓储任务，综合考虑任务分配与路径规划，提出一种高效率、高灵活性的仓储多机器人系统设计方案。引入交通流量预测对传统拍卖算法进行改进，优化任务分配，减少仓储环境内机器人交通阻塞现象，以期实现系统效率的提升。针对路径规划问题，采用Floyd算法结合交通规则进行优化，降低机器人碰撞风险，提高系统安全性和稳定性。此外，将虚拟结构编队技术引入仓储多机器人系统设计，使得系统能够处理混杂单机与多机编队仓储任务。在MATLAB平台进行仿真实验，验证本研究所设计算法的有效性和可行性。

1 相关工作

1.1 仓储多机器人系统

基于多机器人协作设计的仓储多机器人系统，可令多个机器人共同协作完成仓储任务，该系统具有高灵活性、高效率和低成本等优点。Jose等[2]为3个机器人在基于仓储环境的共同工作空间中的任务分配和无碰撞路径规划提出了一种启发式方法。国内外涌现出了一些专注于智能仓储的企业，亚马逊基于Kiva机器人构建的无人仓库系统为最具代表性的案例[3–4]。该系统利用仓储式移动机器人，实现了从“人到货”到“货到人”的分拣和选取方式的转变，实现了无人化的仓储作业[5]。同时，国内也不断涌现了一些致力于多机器人系统的智能仓储企业，例如快仓、海康等。这些企业通过运用多机器人系统，不但提高了仓储效率，还降低了人力成本，取得了显著的经济效益。而高效的仓储系统依赖着多机器人的任务分配和路径规划技术。

1.2 多机器人系统中的任务分配

任务分配旨在有效地将任务分配给适当的机器人，以实现整体系统的高效运作。多机器人任务分配(multi-robot task allocation, MRTA)可根据机器人同时完成任务数量，划分为单任务机器人(single-task, ST)与多任务机器人(multi-task, MT)，也可根据任务所需机器人数量，划分为单机器人任务(single-robot, SR)与多机器人任务(multi-robot, MR)[6]。目前主流的任务分配算法主要分为市场机制分配法[7]、群体智能启发式算法[8]以及基于深度学习的任务分配算法[9]等几种。Sullivan等[10]引入了新的拍卖竞价和解析算法解决单物品拍卖问题，并将能源消耗和完成任务总时间作为指标。

1.3 多机器人系统中的路径规划

路径规划主要是指机器人在区域内自动规划一条从指定起点到指定终点的路径，且该路径可满足机器人的安全需求和成本需求。多机器人路径规划问题属于NP-hard问题[11]。常用的路径规划算法有Dijkstra算法[12]、RRT算法[13]、Floyd算法等。王靖东[14]提出了一种改进的Floyd算法，通过优化路径选择策略，提高了多机器人系统的路径规划效率。

1.4 多机器人编队技术

多机器人编队控制基本原理是对群体进行行为控制，即控制多个智能体群体的几何形态。在仓储环境下，多机器人编队控制可令多机器人在维持一定队形的行进过程中，安全地避开可能的障碍，从而完成任务。为解决订单中存在的大尺寸货物搬运困难问题，本研究选择将多机器人协同编队技术引入多机器人系统的设计，从而提升单机与多机完成混杂任务的能力。近年来，控制界对多移动机器人编队控制进行了大量的研究[15]。经常使用的编队方法有虚拟结构编队、leader-follower编队[16]、基于行为编队[17]等。虚拟结构编队最早由Tan提出，通过将队形视作刚性结构，实现队形的形成与保持[18]。

2 任务分配策略设计

在仓储多机器人系统中，合理的任务分配策略是实现该系统高效工作的关键[19]。

2.1 单一任务的分配策略

多机器人的任务分配问题可视为最优分配问题。该问题是指如何将多个机器人在约束条件下分配给一组任务，使得完成任务的方式最优，即最大限度地提高系统完成任务的效率。使用拍卖算法可解决多机器人的任务分配问题。该算法基本思想是模拟现实经济市场中的拍卖竞拍过程，机器人作为竞拍者对需要分配的任务进行竞价，根据各机器人的出价高低分配该任务。拍卖算法在任务分配中的具体实现步骤如下：

step1初始化将任务视为拍卖对象，机器人视为竞标者。任务分配中心依据任务优先级发布当前需分配的任务。

step2竞价机器人根据自身状态与任务要求出价。

step3选择确定该任务最高出价者，将该任务分配给出价最高的机器人。

step4结束对未被分配的任务循环该拍卖过程，当所有任务都被分配，结束拍卖过程，完成任务分配。

2.2 仓储环境下的多任务分配策略

本研究以仓储任务为拍卖对象，以机器人为竞标者，以出价成本最低的机器人为中标者。令每个仓储任务根据其在任务组中的先后顺序进行招标。每轮竞标中，所有机器人都会为该任务进行出价。在选择阶段，优先选择出价成本低的机器人。每个机器人拥有一个已分配任务序列，在每轮竞标结束后，更新机器人任务序列和任务集。图 1为拍卖算法流程图。

由于需要系统高效完成仓储任务，各机器人对任务的出价成本与任务完成时间正相关。并且在计算新任务成本时，机器人R_i的任务序列中可能存在还未完成的任务。因此可对机器人R_i的投标成本B_i进行公式化表示。

式中：T_{t, i}表示机器人R_i完成任务序列中所有任务的总时间；T_{d, i}表示机器人R_i完成任务序列中所有任务的运动时间；α表示机器人完成任务总时间对竞价成本的影响度；β表示机器人运动时间与工作时间的相对重要性。另外, 机器人完成任务过程包括机器人前往目标点的运动过程以及机器人在任务点的工作过程。由T_{w, i}表示机器人R_i在任务序列中所有任务点的工作时间, 可将机器人R_i完成所有任务的总时间T_{t, i}表示为

将机器人在该环境中的运动速度表示为v, 在每个任务点的工作时间表示为t_w。机器人R_i完成任务序列中所有任务的运动路径长度表示为S_{d, i}, 其任务序列中所有任务的任务点总个数为n_{c, i}, 则可得到以下公式

当需要编队协同完成的任务作为拍卖对象时, 系统需要组成编队机器人的总成本最小化。因此, 在上述算法的框架下, 对于需要多机器人协同完成的任务, 系统会分配给总成本最低的3个机器人。具体步骤为: 首先根据上述算法为该任务找到成本最低的机器人, 再使用该算法找到到达第一个任务点成本最低的另外2个机器人, 以确保成本最小化同时实现编队协同作业。

另外, 根据公式(3)可知, 机器人执行任务的成本计算需要基于其全局路径规划的结果, 后文将详细讨论路径规划策略的设计。

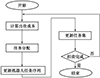图1

拍卖算法流程图

2.3 考虑交通流量预测的任务分配策略

仓储环境下的多机器人系统需要高效完成复杂的搬运任务。然而, 在一定空间中使用较多数量的机器人时, 仓储环境中的某些区域可能由于多个机器人集中, 使得机器人密度过大, 引起交通拥堵或死锁问题。针对该问题, 本研究考虑区域内机器人流量, 在拍卖算法中引入交通流量影响因子, 可以更准确地评估机器人执行任务的实际成本。

因此, 将交通流量影响因子x_i加入机器人R_i的成本计算, 可更新其投标成本计算为

本研究将机器人R_i途径各区域的交通流量F_i作为影响竞价成本的因素, 令ζ表示区域交通流量对竞价成本的影响度, 则该机器人对应交通流量影响因子x_i可表示为

将仓储环境划分为m个区域, 令S_p表示区域a_p的面积。得到机器人R_i完成该任务的路径后, 从路径中每隔h取一个路径点, 可得到机器人R_i位于所取路径点时, 当前所在区域a_p的机器人数量为N_p¹(i), N_p²(i), N_p³(i), …。则可计算该机器人经过该区域时交通流量的峰值N_{p, max}(i)为

则机器人R_i经过区域a_p峰值密度为

机器人R_i路径区域的流量可表示为

3 路径规划策略设计

在解决多机器人的路径规划问题时, 除了考虑机器人与环境中静态障碍物的碰撞问题, 还需考虑机器人之间的相互碰撞问题。因此, 本节针对仓储多机器人系统提出一种2层路径规划策略, 外层负责全局路径规划, 内层负责局部路径规划, 以确保多机器人高效、安全地协同完成仓储任务。另外, 针对混合多机器人协同搬运任务的需求, 本节基于虚拟结构法进行编队建模。

3.1 考虑多机器人协同搬运的全局路径规划

在全局路径规划算法中, Floyd算法能够计算给定加权图中任意点之间的最短路径。相比于只能计算给定图中单源最短路径的Dijkstra算法, 该算法不需要对每个节点进行单独计算[20]。另外, PRM算法、RRT算法等基于采样的路径规划算法, 性能依赖于采样密度等参数的选择, 大型仓储环境中的采样点较多, 计算量较大。Floyd算法基于图论进行路径规划, 可以保证全局最优性和较高的环境适应度。此外，本文研究环境为仓储环境, 该环境中货架和通道固定, 不需不断更新算法。因此本文采用的Floyd算法的计算复杂度不影响任务分配过程。

该算法应用邻接矩阵G、距离矩阵D和路径矩阵P, 为机器人规划最优路径。矩阵G表示图中各节点之间的直接连接关系; 矩阵D表示节点之间的最短路径距离; 矩阵P存储各节点之间最优路径的前驱节点。本研究中Floyd算法的基本步骤如下:

step1 初始化邻接矩阵G: 在本研究中根据所设置的仓储环境对该矩阵进行初始化。

step2 初始化距离矩阵 D和路径矩阵P: 遍历矩阵G, 并将矩阵 G中的值复制到对应位置的矩阵D中。同时, 将矩阵P中的元素初始化为-1。

step3 更新距离矩阵 D和路径矩阵P: 针对每个节点k, 遍历所有节点i和节点j, 若通过节点k能够得到的路径长度比当前记录的路径长度更短, 则更新矩阵 D和路径矩阵P。

step4 重复step3，直到遍历完所有节点k。

3.2 多机器人编队模型设计

在编队搬运货物时, 队形的稳定性对于保证货物运输的安全性至关重要。虚拟结构编队法(virtual structure)的基本思想是将编队队形视作刚体结构, 每个机器人位于虚拟结构的固定顶点。当队形移动时, 机器人跟随对应刚体固定点运动, 通过控制虚拟结构的位置和方向间接控制机器人的运动。该编队控制方法使得编队队形较为固定, 可确保大尺寸货物运输时的稳定安全。因此, 针对多机器人协同搬运任务, 本文设计了一种基于虚拟结构编队法的三机器人编队模型。

在本文仓储环境下, 由于虚拟结构为刚性结构, 在规划全局路径时将编队内的多机器人视为整体进行规划, 即为虚拟结构中心点规划全局路径, 再根据虚拟结构的几何结构为其结构上各顶点的机器人规划路径。图 2为虚拟结构编队图。

设定使用3个机器人组成正三角形编队, 可得公式(9)。

其中虚拟结构中心点表示为(x_VS, y_VS), 参与编队的机器人坐标(x_i, y_i), i表示机器人的索引, D_f为机器人与虚拟结构中心点的期望距离, θ_i表示为各机器人相对于虚拟结构中心点的期望角度。

为实现对编队机器人的路径规划, 本研究将单任务机器人解决多机器人任务(ST-MR)问题转化为单任务机器人解决单机器人任务(ST-SR)问题, 再通过上述Floyd算法进行解决。图 3为路径规划流程图。

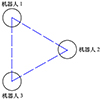图2

虚拟结构编队图

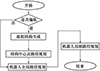图3

路径规划流程图

3.3 解决机器人冲突问题的局部路径规划

全局路径规划算法为每个机器人生成了完成当前订单任务的路径, 各机器人生成的路径相互独立。由于仓储环境中机器人通道采用了双向通道, 机器人遵循通道中单向运动的原则, 机器人之间的碰撞冲突大大减少。

在上述基础上, 仍然可能存在碰撞情况, 可能的碰撞主要有交叉碰撞和追尾碰撞。追尾碰撞现象出现于同向通道, 交叉碰撞现象则出现于交叉路口。由于存在单机与编队共存的状态, 碰撞还可分为单机与单机碰撞、单机与编队碰撞、编队与编队碰撞。6种碰撞类型如图 4所示。

对于机器人R_i, 其在t时刻的位置为Qⁱ(t)。由于单机与单机、单机与编队、编队与编队的安全距离不同, 分别设置对应的安全距离ε₁, ε₂和ε₃。该系统中机器人有3种任务执行状态, 将其用X表示。若机器人R_i在t时刻处于运动状态时X_i(t)=1, 处于工作状态时X_i(t)=2, 处于停止状态时X_i(t)=3。机器人所执行的任务类型用Y表示, Y_i=1表示机器人R_i执行单机器人任务, Y_i=2表示机器人R_i执行多机器人编队任务。机器人R_i在t时刻的运动方向为M_i(t), 执行的任务序号为D_i(t)。因此关于3种追尾碰撞, 单机与单机之间追尾碰撞可定义为

单机与多机编队之间追尾碰撞可定义为

多机编队与多机编队之间追尾碰撞可定义为

参考十字路口的交通规则, 将该仓储环境中每个通道交叉处划分成路口外区域与路口内区域。第w个路口的路口外区域表示为O_w、路口内区域表示为I_w。关于3种交叉碰撞, 单机与单机之间交叉碰撞可定义为

单机与多机编队之间交叉碰撞定义为

多机编队与多机编队之间交叉碰撞定义为

若满足上述碰撞定义, 则c(i, j)=1, 表示机器人R_i与机器人R_j之间存在碰撞, 否则不存在碰撞。根据上述碰撞设置交通规则, 若c(i, j, t+Δt)=1且发生碰撞类型为追尾碰撞, 则令追尾者停止运动进行避让, 被追尾者继续运动, 直到不存在碰撞即c(i, j)=0。若c(i, j, t+Δt)=1且发生碰撞类型为交叉碰撞, 则令机器人R_i到达路口外时停止运动, 等待机器人R_j离开路口, 直到满足c(i, j)=0。其中c(i, j, t+Δt)=1表示机器人R_i与机器人R_j会在t+Δt时刻出现碰撞情况。

图4

碰撞示意图

4 实验结果分析与总结

4.1 实验环境设置

本研究基于MATLAB平台进行仿真实验。根据文献[21]研究并参考实际仓储环境，使用栅格法创建仓储环境地图，如图 5所示。

该仓储环境中包含货架、机器人、机器人停放站、机器人通道、订单货物接收点。其中，货架5行6列，共计30个，每个货架拥有3个取货位。该环境中机器人通道设定为对向双通道，通道中机器人遵循靠右行驶原则。单通道中可容纳3个机器人编队通过，避免机器人之间的部分冲突。货架外围共18个机器人停放站，每个机器人停放站只有一个出口和入口，能停放6个机器人，机器人可在机器人停放站进行停放或充电等工作。环境中共有18个机器人，初始时分别停放在18个停放站中，每个机器人直径为0.4 m，设置机器人编队队形为边长0.4 m的正三角形。仓储环境划分6个区域如图 6所示。

图5

仓储环境图

图6

仓储环境区域划分图

4.2 实验结果与分析

1) 单机与多机编队协同完成仓储任务的实现

本研究在仓储环境下实现了基于拍卖算法的任务分配与基于Floyd算法的路径规划多机器人系统。该系统旨在优化机器人在仓储环境中的任务执行效率和协同能力。每个任务具有任务点和目标点，任务点为订单取货地点，目标点为订单货物接收地点，被分配机器人需要前往任务点执行拾取操作并最终将货物搬运至目标点。本研究中设定了6个仓储任务，其中有3个任务需要编队搬运完成，另外3个由单机器人独立完成。具体任务要求如表 1所示。

在仿真实验中，系统成功完成上述混合仓储任务，仿真实验结果如图 7所示。图中*号表示该订单中需要在货架上拾取货物的工作点，五角星表示该订单的货物接收点，不同颜色的虚线分别代表不同机器人的运动路径，清晰地展示了机器人在执行任务过程中的协同方式。

对于需要多机器人协同的任务，机器人能够通过编队方式共同完成大件货物搬运，体现了系统在协同作业中的优势。对于单机器人任务，机器人则独立完成指定任务，展示了系统的灵活性和高效性。综上所述，本研究所实现的多机器人系统在仓储环境下能够灵活应对单机任务和多机协同任务，为实际仓储管理中多机器人系统的应用提供了有效的解决方案。

2) 基于交通规则约束优化路径规划的实验结果与分析

根据上述任务组的任务设定，本文设计了2组实验评估交通规则约束对机器人路径规划的影响，分别为未加入交通规则约束的情况和加入交通规则约束的情况。实验结果如图 8所示。

图 8展示了随时间变化的机器人之间最小距离，蓝色曲线表示未加入交通规则约束的情况，机器人之间的最小距离小于0.5 m，即机器人之间存在多次碰撞风险。红色曲线表示加入交通规则约束的情况，机器人之间的最小距离始终大于0.6 m，明显降低了碰撞风险。这是由于机器人在同一通道或交叉路口运动时能够保持一定的安全距离，能够确保各自路径不发生冲突。

通过对比可明显看出，加入交通规则约束后，机器人之间的碰撞情况减少。且在大多时间内，红色曲线明显高于蓝色曲线，表明交通规则约束的效果显著。综合上述实验结果，通过引入交通规则，机器人能够在复杂环境中更安全、更高效地完成任务，显著降低碰撞风险，提高了系统的可靠性。

3) 基于交通流量预测优化任务分配的实验结果与分析

令仓储系统生成8个仓储任务，各个任务具体要求如表 2所示。

根据前述内容，本文将机器人完成任务总时间对竞价成本的影响权重设定为0.5，并将机器人运动时间与工作时间的相对重要性权重设定为0.5。在未加入交通流量影响因子的情况下，上述任务的任务分配结果如表 3所示。

根据任务分配策略，对于需要3个机器人编队完成的任务T8，将计算得到成本最低的机器人R5初步分配给该任务，机器人R5完成任务需花费的成本为69.50。后续将到达编队任务点成本最低的2个机器人R2和R6分配给该任务，机器人R2和机器人R6到达编队点成本分别为26.75与25.25。在未加入交通流量预测情况下，任务T8的完成时间为88.40 s。根据上述分配方案，多机器人完成任务T8的路径如图 9所示。

为上述实验加入交通流量预测，其他条件不变，其中区域交通流量对竞价成本的影响权重设定为100，根据任务分配策略，分配结果如表 4所示。

分配任务T8时，将成本最低的机器人R5初步分配给该任务，该机器人成本为73.94。由于在分配过程中加入了交通流量影响因子，导致到达编队任务点成本最低的另外2个机器人变更为机器人R6和机器人R17，成本分别为34.14和33.81。因此，任务T8最终被分配给机器人R5、R6、R17，3个机器人完成任务T8的路径如图 10所示。

在上述情况下，任务T8完成时间为87 s，相比于未考虑交通流量影响的情况，减少了1.4 s。这是由于多机器人系统在分配仓储任务时，综合评估了交通流量，从而最优地选择其他机器人来执行任务，减少任务完成时间。这种任务分配优化使得机器人能够避开拥堵的区域，可有效减少机器人在密集区域的停滞和等待时间，提高作业效率。

任务组具体要求表

实验结果图

随时间变化的机器人之间最小距离图

交通流量预测任务组具体要求表

未加入交通流量预测的任务分配表

未加入交通流量影响情况下完成任务T8的路径图

表4

加入交通流量预测的任务分配表

图10

加入交通流量影响情况下完成任务T8的路径图

4.3 研究工作总结

本研究针对需单机单独完成和多机协同完成的混合仓储运输任务，提出了一种多机器人系统的任务分配与路径规划策略。在任务分配策略方面，基于拍卖算法进行任务分配，并加入交通流量影响因子对拍卖算法进行改进。在路径规划策略方面，加入基于虚拟结构编队法的三机器人编队模型，并提出了2层路径规划策略：外层基于Floyd算法实现全局路径规划，内层设计避碰规则实现局部路径规划。

在仿真实验中验证了所提出的任务分配与路径规划策略。实验结果表明，系统能够处理2种类型的混杂任务，并充分展示了其高效性和灵活性。加入交通规则约束减少了机器人之间的碰撞风险，提高了系统的整体效率和任务完成的安全性。通过引入交通流量预测对任务分配进行优化，使机器人在执行任务时能够智能避开拥堵区域，避免了机器人在区域内的过度集中造成交通堵塞和停滞等待，显著提高了作业效率。

综上所述，本研究对多机器人系统进行多方面优化，实现了混杂单机与多机编队仓储任务的高效完成，并证明了该系统的实际应用价值，也为未来多机器人系统在仓储管理中的广泛应用提供了坚实的理论和实践基础。

5 结语

尽管本研究在多机器人任务分配与路径规划方面取得了一定成果，但仍有许多可以进一步研究和改进的地方。例如，可以扩展任务种类，探索更多类型仓储任务的分配与执行策略。另外，当前本研究采用了双通道路网以降低机器人碰撞的可能性，但因此可能造成仓储货物存储量减少。因此，可以针对单通道环境开发更复杂的避碰算法，以平衡货物存储量与系统的安全性之间关系。此外，还可深入研究如何在更复杂的仓储环境下优化机器人协作，提高系统的灵活性与适应性。

References

YAMASHITA A, ARAI T, OTA J, et al. Motion planning of multiple mobile robots for cooperative manipulation and transportation[J]. IEEE Trans on Robotics and Automation, 2003, 19(2): 223–237. [Article] [CrossRef] [Google Scholar]
JOSE K, PRATIHAR D K. Task allocation and collision-free path planning of centralized multi-robots system for industrial plant inspection using heuristic methods[J]. Robotics & Autonomous Systems, 2016, 80: 34–42 [CrossRef] [Google Scholar]
GUO Hao. Intelligent warehousing improves warehousing logistics[J]. China Storage & Transport, 2017(3): 71 (in Chinese) [Google Scholar]
ENRIGHT J J, WURMAN P R. Optimization and coordinated autonomy in mobile fulfillment systems[C]//Workshops at the twenty-fifth AAAI Conference on Artificial Intelligence, 2011: 33–38 [Google Scholar]
LUO Xuedong. Multi-robot path planning and scheduling for intelligent warehouse[D]. Chongqing: Chongqing Post and Communications University, 2022 (in Chinese) [Google Scholar]
GERKEY P, MATARID J. A formal analysis and taxonomy of task allocation in multi-robot systems[J]. The International Journal of Robotics Research, 2004, 23(9): 939–954. [Article] [CrossRef] [Google Scholar]
SKALTSIS G M, SHIN H S, TSOURDOS A. A survey of task allocation techniques in MAS[C]//2021 International Conference on Unmanned Aircraft Systems, 2021: 488–497 [Google Scholar]
LIU Shuhua, ZHANG Yu, WU Hongyan, et al. Multi-robot task allocation based on swarm intelligence[J]. Journal of Jilin University, 2010, 40(1): 123–129 (in Chinese) [Google Scholar]
ZHANG Ziyin, CHEN Yunfei, WANG Yuhua, et al. Multi-robot task allocation algorithm based on heuristically accelerated deep Q network[J]. Journal of Harbin Engineering University, 2022, 43(6): 857–864 (in Chinese) [Google Scholar]
SULLIVAN N, GRAINGER S, CAZZOLATO B. Sequential single-item auction improvements for heterogeneous multi-robot routing[J]. Robotics and Autonomous Systems, 2019, 115(8): 130–142 [CrossRef] [Google Scholar]
ALMADHOUN R, TAHA T, SENEVIRATNE L, et al. A survey on multi-robot coverage path planning for model reconstruction and mapping[J]. SN Applied Sciences, 2019, 1(8): 1–24 [Google Scholar]
ALSHAMMREI S, BOUBAKER S, KOLSI L. Improved Dijkstra algorithm for mobile robot path planning and obstacle avoidance[J]. Computers, Materials and Continua, 2022, 72: 5939–5954. [Article] [CrossRef] [Google Scholar]
QI J, YANG H, SUN H. MOD-RRT^*: a sampling-based algorithm for robot path planning in dynamic environment[J]. IEEE Trans on Industrial Electronics, 2020, 68(8): 7244–7251 [Google Scholar]
WANG Jingdong. Path planning for an indoor robot with optimized floyd algorithm-based[D]. Xi'an: Northwest Agriculture and Forestry University, 2015 (in Chinese) [Google Scholar]
OH K K, PARK M C, AHN H S. A survey of multi-agent formation control[J]. Automatica, 2015, 53: 424–440. [Article] [Google Scholar]
HAN T, GUAN Z H, CHI M, et al. Multi-formation control of nonlinear leader-following multi-agent systems[J]. ISA Transactions, 2017, 69: 140–147. [Article] [CrossRef] [Google Scholar]
LEE G, CHWA D. Decentralized behavior-based formation control of multiple robots considering obstacle avoidance[J]. Intelligent Service Robotics, 2018, 11: 127–138. [Article] [CrossRef] [Google Scholar]
LEWIS M A, TAN K H. High precision formation control of mobile robots using virtual structures[J]. Autonomous Robots, 1997, 4(4): 387–403. [Article] [CrossRef] [Google Scholar]
ZHANG Zhongwei, GAO Zengen, WANG Jingrui, et al. Review and development trend analysis of distributed AGV scheduling[J]. Manufacturing Technology & Machine Tool, 2024, 74(5): 1–10 (in Chinese) [Google Scholar]
SHI Y, HU B, HUANG R. Task allocation and path planning of many robots with motion uncertainty in a warehouse environment[C]//IEEE International Conference on Real-time Computing and Robotics, 2021: 776–781 [Google Scholar]
RYU K, DANTANARAYANA L, FURUKAWA T, et al. Grid-based scan-to-map matching for accurate 2D map building[J]. Advanced Robotics, 2016, 30(7): 431–448. [Article] [CrossRef] [Google Scholar]

All Tables

任务组具体要求表

交通流量预测任务组具体要求表

未加入交通流量预测的任务分配表

加入交通流量预测的任务分配表

All Figures

	图1 拍卖算法流程图
In the text

	图2 虚拟结构编队图
In the text

	图3 路径规划流程图
In the text

	图4 碰撞示意图
In the text

	图5 仓储环境图
In the text

	图6 仓储环境区域划分图
In the text

	图7 实验结果图
In the text

	图8 随时间变化的机器人之间最小距离图
In the text

	图9 未加入交通流量影响情况下完成任务T8的路径图
In the text

	图10 加入交通流量影响情况下完成任务T8的路径图
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] YAMASHITA A, ARAI T, OTA J, et al. Motion planning of multiple mobile robots for cooperative manipulation and transportation[J]. IEEE Trans on Robotics and Automation, 2003, 19(2): 223–237. [Article] [CrossRef] [Google Scholar]

[2] JOSE K, PRATIHAR D K. Task allocation and collision-free path planning of centralized multi-robots system for industrial plant inspection using heuristic methods[J]. Robotics & Autonomous Systems, 2016, 80: 34–42 [CrossRef] [Google Scholar]

[3] GUO Hao. Intelligent warehousing improves warehousing logistics[J]. China Storage & Transport, 2017(3): 71 (in Chinese) [Google Scholar]

[4] ENRIGHT J J, WURMAN P R. Optimization and coordinated autonomy in mobile fulfillment systems[C]//Workshops at the twenty-fifth AAAI Conference on Artificial Intelligence, 2011: 33–38 [Google Scholar]

[5] LUO Xuedong. Multi-robot path planning and scheduling for intelligent warehouse[D]. Chongqing: Chongqing Post and Communications University, 2022 (in Chinese) [Google Scholar]

[6] GERKEY P, MATARID J. A formal analysis and taxonomy of task allocation in multi-robot systems[J]. The International Journal of Robotics Research, 2004, 23(9): 939–954. [Article] [CrossRef] [Google Scholar]

[7] SKALTSIS G M, SHIN H S, TSOURDOS A. A survey of task allocation techniques in MAS[C]//2021 International Conference on Unmanned Aircraft Systems, 2021: 488–497 [Google Scholar]

[8] LIU Shuhua, ZHANG Yu, WU Hongyan, et al. Multi-robot task allocation based on swarm intelligence[J]. Journal of Jilin University, 2010, 40(1): 123–129 (in Chinese) [Google Scholar]

[9] ZHANG Ziyin, CHEN Yunfei, WANG Yuhua, et al. Multi-robot task allocation algorithm based on heuristically accelerated deep Q network[J]. Journal of Harbin Engineering University, 2022, 43(6): 857–864 (in Chinese) [Google Scholar]

[10] SULLIVAN N, GRAINGER S, CAZZOLATO B. Sequential single-item auction improvements for heterogeneous multi-robot routing[J]. Robotics and Autonomous Systems, 2019, 115(8): 130–142 [CrossRef] [Google Scholar]

[11] ALMADHOUN R, TAHA T, SENEVIRATNE L, et al. A survey on multi-robot coverage path planning for model reconstruction and mapping[J]. SN Applied Sciences, 2019, 1(8): 1–24 [Google Scholar]

[12] ALSHAMMREI S, BOUBAKER S, KOLSI L. Improved Dijkstra algorithm for mobile robot path planning and obstacle avoidance[J]. Computers, Materials and Continua, 2022, 72: 5939–5954. [Article] [CrossRef] [Google Scholar]

[13] QI J, YANG H, SUN H. MOD-RRT^*: a sampling-based algorithm for robot path planning in dynamic environment[J]. IEEE Trans on Industrial Electronics, 2020, 68(8): 7244–7251 [Google Scholar]

[14] WANG Jingdong. Path planning for an indoor robot with optimized floyd algorithm-based[D]. Xi'an: Northwest Agriculture and Forestry University, 2015 (in Chinese) [Google Scholar]

[15] OH K K, PARK M C, AHN H S. A survey of multi-agent formation control[J]. Automatica, 2015, 53: 424–440. [Article] [Google Scholar]

[16] HAN T, GUAN Z H, CHI M, et al. Multi-formation control of nonlinear leader-following multi-agent systems[J]. ISA Transactions, 2017, 69: 140–147. [Article] [CrossRef] [Google Scholar]

[17] LEE G, CHWA D. Decentralized behavior-based formation control of multiple robots considering obstacle avoidance[J]. Intelligent Service Robotics, 2018, 11: 127–138. [Article] [CrossRef] [Google Scholar]

[18] LEWIS M A, TAN K H. High precision formation control of mobile robots using virtual structures[J]. Autonomous Robots, 1997, 4(4): 387–403. [Article] [CrossRef] [Google Scholar]

[19] ZHANG Zhongwei, GAO Zengen, WANG Jingrui, et al. Review and development trend analysis of distributed AGV scheduling[J]. Manufacturing Technology & Machine Tool, 2024, 74(5): 1–10 (in Chinese) [Google Scholar]

[20] SHI Y, HU B, HUANG R. Task allocation and path planning of many robots with motion uncertainty in a warehouse environment[C]//IEEE International Conference on Real-time Computing and Robotics, 2021: 776–781 [Google Scholar]

[21] RYU K, DANTANARAYANA L, FURUKAWA T, et al. Grid-based scan-to-map matching for accurate 2D map building[J]. Advanced Robotics, 2016, 30(7): 431–448. [Article] [CrossRef] [Google Scholar]