EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 3 (June 2025) JNWPU, 43 3 (2025) 555-563 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 3, June 2025
Page(s) 555 - 563
DOI https://doi.org/10.1051/jnwpu/20254330555
Published online 11 August 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

机载卫星转动平台的可靠性对卫星系统的稳定运行起着决定性作用。转动平台依赖于多种活动线缆[1]进行电力和数据的传输, 活动线缆的布线设计决定了电力和数据的传输可靠性。如果活动线缆布线设计不合理, 会导致活动线缆在运动过程中出现过度拉伸扯断、夹伤、疲劳[2]、外皮磨损、与结构件发生缠绕[3]等问题, 从而可能导致卫星系统性能下降, 甚至可能引起严重的安全事故[4]。通过对转动平台上活动线缆运动过程模拟, 能够提前发现和避免运动过程中出现以上问题。线缆物理特性模型的求解是活动线缆运动过程模拟的前提。

目前, 线缆物理特性模型的求解技术主要包括有限差分法[5-6]、非线性有限元法[7-9]及L-M算法[10-12]。

Lundquist等[5]将有限差分法应用于电气线缆模拟领域, 该算法能较好地处理电气线路这类模型约束较少的问题, 但由于活动线缆物理特性模型参数多, 使用有限差分法法求解会导致模型求解困难、甚至无法求解。此外, 该方法难以直接处理线缆物理特性模型的边界约束[12], 需要借助其他优化方法, 例如拉格朗日乘子法或消元法, 这样会进一步导致模型求解困难。

为了直接处理边界约束, Rizzo等[7]采用非线性有限元法处理复杂的材料行为和边界约束。该方法通过模拟材料的应力和应变关系以及考虑材料的非线性, 有效地解决了边界约束问题。然而, 由于其涉及到的计算量通常很大, 在求解活动线缆物理特性模型时, 这种方法的计算成本变得难以承受。

Lü等[12]创新地结合了高斯牛顿与梯度下降特性的L-M算法, 通过构造最小化残差的目标函数, 有效处理了边界约束问题, 同时在求解精度和求解效率上取得平衡。该算法的流程为从初始解(初始搜索点)出发, 使用阻尼系数调整高斯牛顿下降与梯度下降的比例, 最终收敛到最优解。该算法不仅能在较短的时间内完成求解, 还能保持较高的精度。

然而, 通过研究发现, L-M算法的初始解选取依赖于经验, 需要耗费大量时间调参, 导致求解效率低。此外, 由于线缆物理特性模型的梯度图存在多个谷值和鞍点[13], 而该算法的阻尼系数更新策略固定不变, 导致模型的求解精度不高。

为此, 本文基于活动线缆几何特征, 提出了一种基于悬链线方程[14]的初始解生成方法, 以及一种根据最近2次迭代的评分平方商自适应更新阻尼系数的策略, 并在此基础上提出了改进的L-M算法。实验结果表明, 改进的L-M算法与现有L-M算法相比, 在求解精度和效率上均有明显优势。

1 转动平台上活动线缆物理特性建模

为了精确仿真活动线缆的位姿, 选择适合的物理模型至关重要。本文选用Lü等[12]提出的弹性细杆模型, 该模型的弹性特性可以很好地描述活动线缆在各种载荷下展现出的弯曲和扭转行为。

弹性细杆模型的应用可以简单地分为三部分：①准确分析活动线缆受力平衡情况, 建立Kirchhoff平衡方程; ②找到线缆物理特性模型的边界约束; ③联立Kirchhoff平衡方程和边界条件, 构造非线性优化问题的目标函数。

本文仅引用了部分相关的符号和公式, 具体模型见文献[12]。

设活动线缆分成n段, xt=(x1t, x2t, …, xit, …, xnt)为活动线缆非线性优化问题的第t次迭代解, x=(x1, x2, …, xi, …, xn)为问题的最优解, 其中xi=(q1, i, q2, i, q3, i, q4, i, Fx, i, Fy, i, Fz, i)。xi中的各个参数解释如下:

1) q1, i, q2, i, q3, i, q4, i为线缆段i的欧拉参数, 用于描述线缆段的旋转姿态;

2) Fx, i, Fy, i, Fz, i为线缆段i所受力在x, y和z方向的分力, 用于描述线缆段在空间中的受力情况。

设问题的约束方程有m个, 第j个方程的表达式为fj(x)=0, 则方程组为f(x)=(f1(x), f2(x), …, fm(x))T= 0。上述方程组的求解问题可以被视为一个非线性优化问题, 其目标函数为

2 改进的L-M法的弹性细杆线缆物理特性模型求解

2.1 现有L-M算法在线缆物理特性模型求解中的问题分析

现有L-M算法[12]在线缆物理特性模型求解中有2个问题: 初始解的设定依赖于经验以及阻尼系数μ的更新因子固定不变。下面分别分析这2个问题对L-M算法求解的影响。

2.1.1 初始解的设定依赖于经验

L-M算法中的初始解是L-M算法的初始搜索点, 合适的初始解使得算法求解精度和求解效率更高。现有的L-M算法采用一种依赖于经验的初始解设定方法, 下面采用多次随机实验模拟依赖于经验的初始解设定策略的效果。表 1为实验的线缆型号及其物性参数。

图 1a)展示了活动线缆实物, 图 1b)显示了通过相机测量得到的活动线缆位姿测量值, 图 1c)~1f)分别表示独立的随机实验50次、100次、200次和1 000次得到的最优解。

thumbnail 图1

不同初始解随机次数的活动线缆三维散点图

由图 1c)~1f)可知, 不同的初始值会导致计算结果差异显著。由图 1c)~1d)的对比可知, 多次基于经验设定初始值有时不一定能提高求解精度。由图 1c)~1f)对比可知, 虽然多次基于经验设定初始值有时能提高求解精度, 但会导致求解效率降低。因此, 依赖于经验的方法不能一定确保求解精度提高, 但会导致求解效率的降低。

表1

实验线缆型号及其物性参数

2.1.2 阻尼系数μ的更新因子固定不变

L-M算法通过解x的残差f(x)来衡量模型拟合的精度, 其中阻尼系数是调控算法迭代步长的关键参数。残差越小, 表明模型拟合度越高, 而阻尼系数则影响每次迭代的调整幅度, 确保算法在收敛速度与精度之间取得平衡。现有的L-M算法采用一种更新因子固定不变的阻尼系数更新策略, 下面采用不同更新因子条件实验来模拟固定不变的更新因子设定策略的效果, 实验线缆参数仍为表 1所示。

图 2展示了在不同更新因子条件下, 随着迭代次数增加, 残差f(x)的变化趋势。

thumbnail 图2

不同更新因子条件下的残差变化图

由图 2可知, 尽管高更新因子(如更新因子为10的红色线)可以加速收敛, 但最终收敛到一个残差较大的局部最优解; 低更新因子(如更新因子为2的蓝色线)在迭代过程中搜索更加仔细, 残差最终较小, 但收敛速度明显较慢, 迭代次数大幅增加, 导致搜索时间过长。因此, 固定不变的更新因子无法同时保证求解精度和求解效率。

2.2 改进的L-M算法

为了克服现有L-M算法在线缆物理特性模型求解中对初始解的依赖以及阻尼系数更新因子固定不变的问题, 本文提出了2种改进策略。首先, 通过基于悬链线方程的方法生成初始解, 减少求解过程对经验的依赖。其次, 引入一种基于评分平方商的自适应阻尼系数更新策略, 使阻尼系数的更新更加灵活和有效, 不局限于固定常数。下文将详细阐述这2种改进策略。

2.2.1 基于悬链线方程的初始解生成方法

张永涛等[14]将悬链线理论应用到线缆建模仿真中, 针对两端固定且仅受重力影响的线缆进行了建模分析, 并取得了良好的装配效果。然而, 由于活动线缆模型采用较传统的三维坐标系统, 存在万向锁问题[15]。特别是当活动线缆旋转角度接近90°时, 会出现轴向奇异性问题, 导致丢失一个旋转自由度, 影响旋转的准确性和连续性。

为此, 本文结合欧拉四元数与悬链线理论, 利用欧拉四元数处理活动线缆旋转中的万向锁问题, 改进活动线缆的动态模拟效果。在此基础上, 提出一种基于悬链线方程的初始解生成方法。生成相应初始解的步骤如下, 示意图如图 3所示。

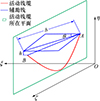thumbnail 图3

三维坐标系下活动线缆示意图

步骤1  输入活动线缆两端坐标值A(ξ1, η1, ζ1)和B(ξ2, η2, ζ2), 线缆长度l, 线缆段数n。

步骤2  计算辅助参数h=η2-η1, 辅助参数\begin{document}$b=\sqrt{\left(\xi_2-\xi_1\right)^2+\left(\zeta_2-\zeta_1\right)^2}$\end{document}。

步骤3  计算悬链线水平张力等效链长a, 其中

步骤4  计算活动线缆所在平面与坐标平面ξ-η之间的夹角θ, 其中

步骤5  若0≤θ≤45°, 活动线缆平面围绕η轴旋转到平行于ξ-η平面的平面上, 活动线缆曲线方程g(ξ)为

式中

步骤6  若45°<θ≤90°, 活动线缆平面围绕η轴旋转到平行于η-ζ平面的平面上, 活动线缆曲线方程g(ξ)为

式中

步骤7  按照等弧长原则计算线缆段中心ξi坐标, 其中ξs为所求弧段起始点横坐标(从ξ1开始), ξe为所求弧段终止点横坐标, 计算公式为

步骤8  将线缆段中心\begin{document}$\xi_{i}$\end{document}坐标代入活动线缆曲线方程\begin{document}$g(\xi)$\end{document}(步骤5)求得\begin{document}$\eta_{i}$\end{document}坐标或\begin{document}$g(\xi)$\end{document}(步骤6)求得\begin{document}$\zeta_{i}$\end{document}坐标, 再进行三维变换可得到对应的\begin{document}$\zeta_{i}$\end{document}或\begin{document}$\eta_{i}$\end{document}, 输出\begin{document}$n$\end{document}段线缆段中心坐标\begin{document}$\left(\xi_{i}, \eta_{i}, \zeta_{i}\right)$\end{document}。

步骤9  将线缆段中心坐标\begin{document}$\left(\xi_{i}, \eta_{i}, \zeta_{i}\right)$\end{document}代入~(8)式 [16]解出初始解\begin{document}$x_{0}$\end{document}。

2.2.2 基于评分平方商的自适应阻尼系数更新策略

在求解活动线缆物理特性模型中, 曲率可以影响搜索方向的选择[17]。为此, 本文提出了基于曲率的自适应阻尼系数更新策略。该策略主要分为两部分：①单次迭代的曲率评分指标建立；②基于曲率评分指标, 采用最近2次迭代评分平方商的阻尼系数更新机制。

1) 曲率评分计算

由第t次迭代的迭代解xt可知, 线缆段i的欧拉参数q1, i, q2, i, q3, i, q4, i, 4个欧拉参数对弧坐标的导数Q1, i, Q2, i, Q3, i, Q4, i。通过这些参数可以将弯扭度w1, i和w2, i表示为

通过弯扭度与曲率的关系[18], 可以求解出曲率ki, 其计算公式为

根据曲率ki为弯曲半径ri的倒数可知, ri的计算公式为

用三点弯曲方法[19]得到最小弯曲半径rmin, 并将各线缆段ri与rmin比较, 比较公式为

将n段线缆段得分Ri加起来, 得到该次迭代的评分Et, 算法结束。第t次的评分公式为

2) 自适应阻尼系数更新策略

在计算每次迭代的曲率评分指标基础上, 采用最近2次迭代评分平方商的阻尼系数更新机制。其在第t次迭代过程中的自适应因子vt为

式中：\begin{document}$E_{t-1}$\end{document}和\begin{document}$E_{t-2}$\end{document}表示第\begin{document}$t-1$\end{document}次的评分和第\begin{document}$t-2$\end{document}次的评分；\begin{document}$v_{\text {min }}$\end{document}和\begin{document}$v_{\text {max }}$\end{document}为更新因子的下限和上限。考虑到\begin{document}$v$\end{document}过小会导致阻尼系数更新较慢, 而过大的\begin{document}$v$\end{document}又会错过可能的最佳搜索方向, 本文令\begin{document}$v_{\text {min }}=2$\end{document}和\begin{document}$v_{\text {max }}=$\end{document} 10, 阻尼系数\begin{document}$\mu$\end{document}的初始值置为1。

当\begin{document}$E_{t-1} \geqslant E_{t-2}$\end{document}时, 即当前迭代的评分高于前一次迭代的评分, 表示最新的解在性能上有所提升。此时, 评分平方商\begin{document}$E_{t-1}^{2} / E_{t-2}^{2} \geqslant 1$\end{document}, 这意味着应当减少阻尼系数的影响, 从而加快收敛速度。

当\begin{document}$E_{t-1}<E_{t-2}$\end{document}时, 表示最新的迭代解的性能下降, 评分平方商\begin{document}$E_{t-2}^{2} / E_{t-1}^{2}>1$\end{document}。这种情况下, 需要增加阻尼系数以引入更多的梯度下降成分, 从而减小步长, 稳定搜索过程, 避免大幅度波动或越过最优解。

具体地, μ的更新方法是

式中, f(xt-1)和f(xt-2)分别是第t-1次的残差和第t-2次的残差。

2.2.3 改进L-M算法的线缆物理特性模型求解伪代码

结合本节的2个改进点: 基于悬链线方程的初始解生成方法和基于评分平方商的自适应阻尼系数更新策略的改进L-M算法如下所示。

L-M算法的输入包括：活动线缆的边界约束方程\begin{document}$\boldsymbol{f}(\boldsymbol{x})$\end{document}、物理特性参数\begin{document}$k_{x, y}, k_{z}, d, \rho, l$\end{document}、根据悬链线方程组计算初始\begin{document}$\boldsymbol{x}_{0}$\end{document}、活动端坐标\begin{document}$A$\end{document}、固定端坐标\begin{document}$B$\end{document}、线缆段数\begin{document}$n$\end{document}。

\begin{document}$\mathrm{L}-\mathrm{M}$\end{document}算法的输出为：计算得到的线缆各微元段的中心点坐标\begin{document}$\boldsymbol{x}$\end{document}。

算法1   改进的Levenberg-Marquardt算法

输入：\begin{document}$\boldsymbol{f}\left(\boldsymbol{x}_{0}\right)=\left(f_{1}\left(\boldsymbol{x}_{0}\right), f_{2}\left(\boldsymbol{x}_{0}\right), \cdots, f_{t}\left(\boldsymbol{x}_{0}\right)\right)^{\mathrm{T}}, k_{x, y}, k_{z}$\end{document}, \begin{document}$d, \rho, \varepsilon_{x}, \varepsilon_{g}, A, B, l, n$\end{document}

输出：\begin{document}$\boldsymbol{x}$\end{document}

1. 根据悬链线方程组计算初始\begin{document}$\boldsymbol{x}_{0}$\end{document}, 令\begin{document}$\mu=\mu_{0}, v=v_{\text {min }}$\end{document}

2. 初始化评分\begin{document}$E_{0}, E_{1}$\end{document}, 最大迭代次数\begin{document}$k_{\text {max }}$\end{document},

3. for \begin{document}$t=1$\end{document} to \begin{document}$k_{\text {max }}$\end{document} do

4.   \begin{document}$g=\boldsymbol{J}(\boldsymbol{x})^{\mathrm{T}} \boldsymbol{f}(\boldsymbol{x})$\end{document}

5.   if \begin{document}$\|g\|<\varepsilon_{g}$\end{document} then

6.     break

7.   end if

8.   while true do

9.：    \begin{document}$\boldsymbol{H}=\boldsymbol{J}(\boldsymbol{x})^{\mathrm{T}} \boldsymbol{J}(\boldsymbol{x})+\mu \boldsymbol{I}$\end{document}

10.      \begin{document}$\Delta \boldsymbol{x}=\boldsymbol{H}^{-1}(-g)$\end{document}

11.      \begin{document}$\boldsymbol{x}=\boldsymbol{x}+\Delta \boldsymbol{x}$\end{document}

12.      \begin{document}$E_{t}=E\left(\boldsymbol{x}_{t}\right)$\end{document}

13.      \begin{document}$D_{t}=F\left(\boldsymbol{x}_{t}\right)$\end{document}

14.      if \begin{document}$\| \Delta \boldsymbol{x}\|<\varepsilon_{x}$\end{document} then

15.        break

16.      end if

17.      if \begin{document}$t>2 \; \& \;E_{t-1} \geqslant E_{t-2}$\end{document} then

18.        \begin{document}$v=\min \left\{\frac{\left(\frac{E_{t-1}^{2}}{E_{t-2}^{2}}+v_{\text {min }}\right)}{2}, v_{\text {max }}\right\}$\end{document}

19.      else

20.        \begin{document}$v=\min \left\{\frac{\left(\frac{E_{t-2}^{2}}{E_{t-1}^{2}}+v_{\min }\right)}{2}, v_{\max }\right\}$\end{document}

21.      end if

22.      if \begin{document}$t>2 \; \& \boldsymbol{f}\left(\boldsymbol{x}_{t-1}\right)>\boldsymbol{f}\left(\boldsymbol{x}_{t-2}\right)$\end{document} then

23.        \begin{document}$\mu=\mu \times v$\end{document}

24.      else

25.        \begin{document}$\mu=\mu / v$\end{document}

26.      end if

27.      \begin{document}$E_{t-2}=E_{t-1}, E_{t-1}=E_{t}$\end{document}

28.      \begin{document}$\boldsymbol{f}\left(\boldsymbol{x}_{t-2}\right)=\boldsymbol{f}\left(\boldsymbol{x}_{t-1}\right), \boldsymbol{f}\left(\boldsymbol{x}_{t-1}\right)=\boldsymbol{f}\left(\boldsymbol{x}_t\right)$\end{document}

29.    end while

30. end for

31. return \begin{document}$\boldsymbol{x}$\end{document}

3 实验结果与分析

3.1 活动线缆仿真实验平台

本文设计了一套实验平台和实验方法用于验证所提出的改进L-M算法的求解精度和求解效率的效果。活动线缆仿真实验平台图 4所示, 包括卫星转动平台和基于双目视觉的活动线缆位姿测量装置。

thumbnail 图4

活动线缆仿真实验平台

其中, 卫星转动平台各组成部分的说明如下:

·传动装置: 用于驱动和控制线缆运动的机械部分;

·活动端A和固定端B: 线缆受运动部件牵引的一端为活动端, 线缆被固定的一端为固定端;

·被测活动线缆: 敷设在转台平台上, 是实验中进行位姿测量的对象;

·转动平面: 机载卫星转动平面, 其转动会牵引活动线缆一起转动, 改变活动线缆位置;

位姿测量装置主体为双目相机，用于捕捉线缆的立体图像, 进行三维重建和位姿测量;

此外, 直流电源为测量系统提供电力的装置, 确保整个测量系统的正常运行。

执行算法的实验平台硬件配置详情如表 2所示。

为评估改进的L-M算法求解精度, 本文采用了标准化均方根误差(ENRMS)作为关键性能指标。通过此指标, 可以将不同算法的预测误差进行无单位的比较, 确保评估的一致性。通过基于双目视觉的活动线缆位姿测量系统测量得出活动线缆各节点的坐标(测量值), 通过算法计算得出活动线缆各节点的坐标(实验值), 将数据代入(16)式可得到求解精度指标ENRMS。

式中：Si为实验值；Oi为测量值。

为获得各测量值坐标，需事先在活动线缆上进行等距标注。如图 4所示, 活动端A到固定端B之间的线缆长度为l, 将线缆长度分为n段, 其等距长度为l/n, 会得到n+1个测量值, 经过位姿测量装置测量各标注点可得到xo, i, yo, i, zo, i; 实验值坐标xs, i, ys, i, zs, i是算法求解结果。

为了更加直观展示实验结果, 使用评价指标P, 其计算公式为

P是介于[0, 1]区间的值, 其值越大表示实验值与测量值越接近, 求解精度越高。为评估改进的L-M算法求解效率, 本文采用了算法的求解时间T作为指标。

本文准备了5根待测线缆, 都是卫星转动平台进行数据传输的常见线缆型号, 物性参数如表 3所示。

同时, 本文采用不同的改进策略组合, 以说明基于悬链线方程的初始解生成方法和自适应的阻尼系数更新策略的有效性, 具体如下:

1) L-M1表示基于经验生成初始解且更新系数不变的L-M算法;

2) L-M2表示基于悬链线生成初始解但更新系数不变的L-M算法;

3) L-M3表示基于经验生成初始解但自适应更新阻尼系数的L-M算法;

4) L-M4表示基于悬链线生成初始解且自适应更新阻尼系数的L-M算法。

表2

实验平台的硬件配置详情

表3

测试线缆型号及其物性参数

3.2 不同策略组合下L-M算法的求解精度实验

本文使用L-M1~4算法, 转动平台在0°~40°范围对各线缆型号的求解精度进行实验。由于实验数据篇幅长, 数据上传至以下链接: https://pan.baidu.com/s/10hp1ZbwzCT8y8VhfpsJI-Q?pwd=np58。

图 5直观地展示了L-M1~4对于不同线缆型号的求解精度。

thumbnail 图5

L-M1~4求解不同线缆型号的精度柱状图

由实验数据可知:

1) L-M1、L-M2、L-M3、L-M4的总平均精度P变化趋势呈逐渐变大的变化趋势;

2) L-M2相较于L-M1的精度提高了8.8%, 这表明引入悬链线方程初始解生成方法后, 算法的初始解精度有了明显改进; L-M3相较于L-M1的精度提高了11.16%, 说明引入自适应更新阻尼系数后, 算法最后能收敛到更优解, 提高了算法的求解精度; L-M4相较于L-M1的精度提高了12.04%, 代表着保持两者结合使用时的协同效应使算法的求解精度进一步提升。

整体而言, L-M2~4的求解精度高于L-M1, 表明结合了悬链线方程的初始解生成方法和自适应阻尼系数更新策略的优点, 能够显著提高L-M算法的求解精度。这种提高不仅在单个线缆型号上表现出色, 而且在多种线缆型号上都保持了一致性, 验证了本文所提算法对线缆物理特性模型求解精度提升的有效性。

3.3 不同策略组合下L-M算法的求解效率实验

表 4给出了L-M1~4求解不同线缆型号的运行时间。由表 4可知, L-M2和L-M4的求解时间在所有线缆型号下均小于L-M1, L-M3的求解时间除RG316G型号外均小于L-M1。这表明本文所提的2个改进策略, 对线缆物理特性模型求解的L-M算法效率提升效果明显。

表4

L-M1~4求解不同线缆型号的时间 s

4 结论

本文针对现有L-M算法初始解的设定依赖于经验的问题, 提出了基于悬链线方程的初始解生成方法; 针对阻尼系数的更新因子固定不变问题, 提出了基于最近2次迭代评分平方商的自适应阻尼系数更新策略。通过搭建活动线缆仿真实验平台并进行实验, 实验结果显示, 在多根线缆型号上, 改进的L-M算法在求解精度和效率上均优于现有求解算法。

本文所提出算法的通用性体现在两方面: ①自适应阻尼系数更新策略能够根据线缆类型的不同参数自适应地调整, 使得算法求解在不同线缆类型上均保持较高的稳定性和精度; ②由于不同线缆类型中的悬链线效应, 具备广泛一致性, 算法中的初始解生成方法和阻尼系数自适应调整能够捕捉这些共性, 进而确保其在不同线缆类型上的适用性。

未来将改进的L-M算法扩展到其他场景的线缆物理特性模型求解, 如柔性机械臂中的柔性杆模型求解, 将是未来研究的重点。

References

  1. LIU J H, ZHAO T, NING R X, et al. Physics-based modeling and simulation for motional cable harness design[J]. Chinese Journal of Mechanical Engineering, 2014, 27(5): 1075–1082 [Google Scholar]
  2. MIYASAKA M, HAGHIGHIPANAH M, LI Y, et al. Modeling cable-driven robot with hysteresis and cable-pulley network friction[J]. IEEE/ASME Trans on Mechatronics, 2020, 25(2): 1095–1104 [Google Scholar]
  3. WANG Y, YAN Z, WU Y F. Numerical simulation of fretting fatigue damage evolution of cable wires considering corrosion and wear effects[J]. Computer Modeling in Engineering & Sciences, 2023, 136(2): 1339–1370 [Google Scholar]
  4. GUO H Z, LI J Y, LIU J, et al. A survey on space-air-ground-sea integrated network security in 6G[J]. IEEE Communications Surveys & Tutorials, 2022, 24(1): 53–87 [Google Scholar]
  5. LUNDQUIST E J, NAGEL J R, WU S, et al. Advanced forward methods for complex wire fault modeling[J]. IEEE Sensors Journal, 2012, 13(4): 1172–1179 [Google Scholar]
  6. LI X L, RUI H X. Stability and convergence based on the finite difference method for the nonlinear fractional cable equation on non-uniform staggered grids[J]. Applied Numerical Mathematics, 2020, 152: 403–421 [Google Scholar]
  7. RIZZO F, KOPP G A, GIACCU G F. Investigation of wind-induced dynamics of a cable net roof with aeroelastic wind tunnel tests[J]. Engineering Structures, 2021, 229: 111569–111575 [Google Scholar]
  8. FAN J Y. Transient thermal analysis of underground power cables using two dimensional finite element method[J]. Microsystem Technologies, 2018, 24(2): 1279–1293 [Google Scholar]
  9. BERTRAND C E, ACARY V, LAMARQUE C H, et al. A robust and efficient numerical finite element method for cables[J]. International Journal for Numerical Methods in Engineering, 2020, 121(18): 4157–4186 [Google Scholar]
  10. LYU W, TAO L M, JI Z N. Sliding mode control of cable-driven redundancy parallel robot with 6 DOF based on cable-length sensor feedback[J]. Mathematical Problems in Engineering, 2017(1): 1928673–1928694 [Google Scholar]
  11. FAN M Y, ZHAO H N, WEN J, et al. A novel calibration method for kinematic parameter errors of industrial robot based on Levenberg-Marquard and beetle antennae search algorithm[J]. Measurement Science and Technology, 2023, 34(10): 105024–105035 [Google Scholar]
  12. LYU N J, LIU J H, XIA H X, et al. A review of techniques for modeling flexible cables[J]. Computer-Aided Design, 2020, 122: 102826–102842 [Google Scholar]
  13. O'LEARY D P, RUST B W. Variable projection for nonlinear least squares problems[J]. Computational Optimization and Applications, 2013, 54: 579–593 [Google Scholar]
  14. ZHANG Yongtao, YAN Jing, ZUO Dunwen, et al. Cable assembly simulation modeling under suspended condition[J].Journal of System Simulation, 2013, 25(7): 1513–1517 (in Chinese) [Google Scholar]
  15. LIU X C, YANG Y N, MA C X, et al. Real-time visual tracking of moving targets using a low-cost unmanned aerial vehicle with a 3-axis stabilized gimbal system[J]. Applied Sciences, 2020, 10(15): 5064–5091 [Google Scholar]
  16. LIU Jianhua, ZHAO Tao, WANG Chunsheng, et al. Motional cable harness physical characteristic oriented modeling and kinetic simulation technology in virtual environment[J]. Journal of Mechanical Engineering, 2011, 47(9): 117–124 (in Chinese) [Google Scholar]
  17. FU X C, LI J X, WU J, et al. ACE-HGNN: adaptive curvature exploration hyperbolic graph neural network[C]//2021 IEEE International Conference on Data Mining, 2021: 111–120 [Google Scholar]
  18. LIU Yanzhu. Nonlinear mechanics of thin elastic rod[M]. Beijing: Tsinghua University Press, 2006 (in Chinese) [Google Scholar]
  19. SALEH R, BARTH M, EBRHARDT W, et al. Bending setups for reliability investigation of flexible electronics[J]. Micromachines, 2021, 12(1): 78–100 [Google Scholar]

All Tables

表1

实验线缆型号及其物性参数

In the text
表2

实验平台的硬件配置详情

In the text
表3

测试线缆型号及其物性参数

In the text
表4

L-M1~4求解不同线缆型号的时间 s

In the text

All Figures

thumbnail 图1

不同初始解随机次数的活动线缆三维散点图
In the text
thumbnail 图2

不同更新因子条件下的残差变化图
In the text
thumbnail 图3

三维坐标系下活动线缆示意图
In the text
thumbnail 图4

活动线缆仿真实验平台
In the text
thumbnail 图5

L-M1~4求解不同线缆型号的精度柱状图
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.