EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 3 (June 2025) JNWPU, 43 3 (2025) 546-554 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 3, June 2025
Page(s) 546 - 554
DOI https://doi.org/10.1051/jnwpu/20254330546
Published online 11 August 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

微弱信号通常具有2层含义: ①信号本身的强度较为微弱; ②信号强度相较于背景噪声而言较小。传统的微弱信号检测一般采用滤波的方式来减小背景噪声, 如时间滤波、空间滤波和光谱滤波。在信噪比较低时, 这些方法能够有效地实现较好的信号检测效果。但是, 信号被噪声湮没, 或者信号与噪声频率相同时, 传统的微弱检测方法就无能为力了。然而, 在合适的非线性系统中, 噪声的能量可以向信号传递, 从而有效地提高输出信号的信噪比, 这种现象称为随机共振[1]。随机共振最初于1981年被提出并用于研究气候温度变化, 此后经过数十年的研究, 在光电子学、气象学和生物学等各个领域得到了广泛应用[2-3]。随机共振具有普适性, 且容易与其他非线性检测相结合, 应用范围相比其他弱光信号检测技术更为广泛[4]。能够产生随机共振的效应有许多, 且这些效应具有不同的应用方向, 如双稳态效应可用于重构被加性噪声湮没的脉冲信号, 以此来对微弱脉冲信号进行检测。

双稳态系统的构建方法有很多, 其中之一是将非线性介质置于法布里-珀罗腔内, 后者对前者产生反馈效应, 共同构成所需系统。这种构建双稳态的方式需要使用非线性材料, 传统的非线性材料具有相对较低的非线性系数, 使用这些材料需要非常高的阈值才能产生理想的双稳态。因此, 生成合适的光学双稳态需要具有高非线性系数的材料。石墨烯在太赫兹波段具有较高的非线性系数[5-7], 但其原子薄特性导致相互作用体积相对较小, 稳定性较低, 这限制了石墨烯在非线性领域的应用[8]。近年来, 三维狄拉克半金属(three-dimensional Dirac semimetal, 3D DSM)作为新型奇异拓扑量子材料备受关注[9-13]。由于狄拉克物理学在2D石墨烯和3D DSM中都描述了电荷载流子, 因此也被称为“3D石墨烯”[14]。与石墨烯类似, 3D DSM也在太赫兹波段具有高非线性系数。然而, 与石墨烯相比, 3D DSM具有更高的载流子迁移率、更高的费米速度，更容易制备且有稳定的性能[15-17]。目前, 已经鉴定出许多材料具有3D DSM特性, 包括Cd3As2、PtTe2、Na3Bi、ZrTe5等[18-21]。有关3D DSM构建双稳态的研究有很多, 但很少有研究将其用于构建随机共振系统。

光子晶体(photonic crystals, PhC)中的拓扑边态模(topological edge state mode, TES)因其独特的拓扑保护和局域场增强特性受到人们的广泛关注[22-23]。目前, 构建TES的方法有很多, 如等离子体米颗粒、光波导、手性双曲超材料、光环谐振器、二维光子晶体和三维光子晶体[24-27]。与二维和三维光子晶体相比, 一维光子晶体更容易制造, 并且一维光子晶体也具有局域场增强的效果[28]。局域场增强是指对空间某一区域的场强大幅度增强, 同时对其他区域的场强影响不大的现象。通过增强非线性介质所在区域的电场, 可以进一步降低双稳态系统的阈值, 得到应用范围更广的随机共振系统。

在本文中, 仿真模拟了反射镜3D DSM法布里-珀罗腔随机共振系统以及光子晶体3D DSM法布里-珀罗腔随机共振系统, 并使用它对含噪脉冲信号进行了重构。计算了该随机共振系统中原始输入信号、输入信号以及输出信号的互相关系数和互相关增益, 从而评估不同噪声强度下的信号重构性能。同时还将光子晶体3D DSM法布里-珀罗腔随机共振系统与反射镜3D DSM法布里-珀罗腔随机共振系统进行对比, 以此来评估光子晶体降低随机共振系统阈值的效果。

1 反射镜3D DSM法布里-珀罗腔随机共振系统

1.1 反射镜3D

DSM法布里-珀罗腔本节使用一对普通的反射镜构建光腔。由一对反射率R=0.6的反射镜组成法布里-珀罗腔, 并将3D DSM置于腔的正中间, 如图 1所示。

thumbnail 图1

含有3D DSM的法布里-珀罗腔示意图

3D DSM的厚度dDSM=20 nm, 法布里-珀罗腔的腔长L=300 μm, 并且腔内填充空气。3D DSM位于腔的正中间, 即L=2L1=2L2。为了获得大的非线性系数, 本文采用太赫兹波段的入射光, 令波长λ=300 μm, 入射光垂直于反射镜平面入射, 即入射角θ=0。

3D DSM是光克尔介质, 其线性带内光学电导率如(1)式所示。

式中：\begin{document}$\sigma_{0} \equiv \frac{\mathrm{e}^{2}}{4 \hbar^{2}}, \omega$\end{document}是角频率；\begin{document}$k_{\mathrm{B}}$\end{document}是玻尔兹曼常数；h是约化普朗克常数；\begin{document}$T$\end{document}是温度；\begin{document}$\nu_{\mathrm{F}}$\end{document}是电子的费米速度；\begin{document}$\tau$\end{document}和\begin{document}$E_{\mathrm{F}}$\end{document}分别表示3D DSM的弛豫时间和费米能量；\begin{document}$L_{i_{s}}(z)$\end{document}是多重对数函数。3D DSM的三阶非线性光学电导率如(2)式所示。

本文使用传输矩阵的形式来描述该系统[8], 其传输矩阵如(3)式所示。

采用与二维薄膜层厚度相同的3D DSM, 这种情况下, 其体电导率可以近似等同于表面电导率 [7], 即\begin{document}$\sigma=d_{\mathrm{DSM}}\left(\sigma_{1}+\sigma_{3}|E|^{2}\right)$\end{document}。根据其电导率表达式 [29], 可以得到对应的传输矩阵

式中, \begin{document}$\zeta=d_{\mathrm{DSM}} \mu_{0} c\left(\sigma_{1}+\sigma_{3}\left|E_{t}\right|^{2}\right) / 2$\end{document}。\begin{document}$\boldsymbol{M}_{1}$\end{document}和\begin{document}$\boldsymbol{M}_{2}$\end{document}对应2个反射镜, 其传输矩阵为

式中, \begin{document}$t_{1}, t_{2}$\end{document}和\begin{document}$r_{1}, r_{2}$\end{document}分别为2个反射镜的透射系数和反射系数, \begin{document}$t_{1}=t_{2}=\sqrt{1-R}, r_{1}=r_{2}=\sqrt{R}$\end{document}。空气层的传输矩阵如(6)式所示。

由此可以得到整个系统的透射系数与反射系数

式中，Mij是矩阵M的元素。根据透射系数的定义, 入射电场与透射电场的关系为

式中, \begin{document}$k=\frac{\omega}{c}$\end{document}, 且\begin{document}$k L_{1}=k L_{2}=\frac{k L}{2}={\rm{\mathsf{π}}} 。$\end{document}代入(8)式中, 可以得到人射光强与出射光强的双稳态表达式

(9) 式表明了入射光强与透射光强之间的双稳态关系。不同的系统参数会对系统的双稳态产生影响, 甚至可能会导致无法出现随机共振现象, 因此系统参数的选取十分重要。下面将研究不同参数的选取对系统双稳态的影响。

图 2a)给出了不同费米能量下入射光强度和透射光强度之间的双稳态关系。其他参数: T=300 K, τ=1.0 ps。以费米能量EF=0.2 eV的曲线为例, 对双稳态曲线的特性进行描述。该双稳态曲线入射光强度对应的临界阈值为曲线2个拐点的横坐标, 大小分别为0.89和1.36 MW/cm2。其中0.89 MW/cm2对应低阈值, 1.36 MW/cm2对应高阈值, 高低阈值之间的区域为双稳态区间。以2个拐点为基准, 可以将曲线由下至上分为下支曲线、中间支曲线和上支曲线三部分。曲线的下支和上支是稳定的, 而中间支是不稳定的, 实际中不存在。下支曲线对应系统的低输出模式, 上支曲线对应高输出模式。系统处于低输出或高输出模式取决于入射光强度的变化方向。当低输出模式下入射光强度增加至高阈值以上时, 系统将由低输出模式转变为高输出模式。同样, 当高输出模式下入射光强度降低至低阈值以下时, 系统将由高输出模式转变为低输出模式。利用这一特性, 可以令与噪声叠加的脉冲信号以高输出模式输出, 噪声本身以低输出模式输出, 从而重构含噪脉冲信号。相应地, 重构不同含噪脉冲信号所需的双稳态区域可能会有所不同, 因此需要根据情况调整双稳态。从图 2中可以看出, 随着费米能量的增加, 系统的高低阈值增加, 系统的双稳态区间逐渐扩大。图 2b)给出了不同弛豫时间下入射光强度和透射光强度之间的双稳态关系。其他参数: T=300 K, EF=0.2 eV。可以看出, 虽然系统的高低阈值也随弛豫时间增加而增加, 但双稳态区间却随着弛豫时间的增加而减小, 这一点与费米能量不同。

thumbnail 图2

反射镜光腔中的双稳态关系

不同的费米能量和弛豫时间均会对双稳态系统产生明显影响, 尤其是费米能量可以通过改变介电常数进行调制[30], 有利于对随机共振系统进行调制。

1.2 反射镜3D DSM法布里-珀罗腔随机共振系统

用含有3D DSM的法布里-珀罗腔构建随机共振系统, 如图 3所示, 并使用其对含噪脉冲信号进行重构。

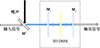thumbnail 图3

基于反射镜3D DSM法布里-珀罗腔的随机共振系统

双稳态系统的参数设置为T=300 K, EF=0.2 eV, τ=1.0 ps。结合双稳态关系以及双稳态随机共振理论, 该随机共振系统的郎之万方程表示为[31]

式中：It为出射光强；V(It)为双稳态系统的势阱函数, 其形式为

Ii为入射光强, 用加入了加性高斯白噪声的脉冲信号作为输入信号, 表示为

式中：\begin{document}$S_{0}$\end{document}是脉冲的峰值强度；\begin{document}$t_{0}$\end{document}是脉冲宽度, \begin{document}$N(t)$\end{document}是满足\begin{document}$\left\langle N\left(t_{1}\right) N\left(t_{2}\right)\right\rangle=2 D \delta\left(t_{1}-t_{2}\right)$\end{document}的加性噪声；\begin{document}$D$\end{document}是噪声强度。通过对郎之万方程求解, 可以得到不同入射光强下对应的出射光强, 进而描绘出不同输入信号下对应的输出信号。

图 4显示了不同噪声下的输入信号以及对应重构后的输出信号。其中图 4a)~4d)对应的含噪脉冲信号的噪声强度分别为0, 0.7, 0.9, 1.0 MW/cm2。图 4e)~4h)分别对应图 4a)~4d)重构后的输出信号。

thumbnail 图4

不同噪声强度下的输入信号及对应的输出信号(脉冲信号强度0.4 MW/cm2, 噪声强度0~1.0 MW/cm2)

为了避免“临界慢化”现象[32], 需要考虑脉冲宽度以及系统最长本征时间。在实验中, 为保证观察到双稳态现象, 需确保入射光强从0逐渐增强至最大值再逐渐减弱至0的时间为系统最长本征时间的100~1 000倍。若时间不足, 系统慢化过快, 可能导致无法观察到双稳态现象。系统最长本征时间包含了3D DSM对太赫兹波段信号的响应时间以及光腔系统的响应时间。3D DSM在太赫兹波段的响应时间可以达到皮秒量级[33]。光腔腔长为300 μm, 其响应时间同样可以达到皮秒量级, 因此脉冲宽度可以达到纳秒量级。这里脉冲宽度固定为5 ns, 输入脉冲信号S0的强度固定为0.4 MW/cm2。如图 4e)所示, 当噪声强度为0 MW/cm2时, 输出脉冲信号的峰值强度为0.05 MW/cm2, 系统处于低输出模式。当噪声强度增加到0.7 MW/cm2时, 如图 4f)所示, 部分脉冲在噪声的帮助下跳转至高输出模式, 系统处于欠共振状态。从图 4g)中可以看出, 当噪声强度为0.9 MW/cm2时, 所有脉冲在噪声的帮助下跳转至高输出模式, 并且与输入脉冲同步, 此时该系统可以有效地重构脉冲信号。如图 4h)所示, 当噪声强度为1.0 MW/cm2时, 部分噪声自身突破阈值跳转至高输出模式, 系统处于过共振状态, 此时输出脉冲失真且失去与输入信号的一致性。

使用互相关系数CS, S0[34]来评估原始输入信号S0, 输入信号Sin以及输出信号Sout之间的相关性, 其定义如(13)式所示。

互相关增益Cg可以用来衡量信号重构的性能, 其定义为

图 5给出了噪声强度从0~1.2 MW/cm2时对应的互相关系数及互相关增益。互相关增益在噪声强度为0.96 MW/cm2时达到最大, 约为3.2。这证明了该随机共振系统重构含噪脉冲信号的能力。

thumbnail 图5

反射镜光腔随机共振系统中噪声强度与互相关系数及互相关增益的关系

2 光子晶体3D DSM法布里-珀罗腔随机共振系统

在上一节中, 基于反射镜3D DSM法布里-珀罗腔建立了随机共振系统, 最终成功将被噪声淹没的脉冲信号重构。尽管该系统可以有效重构脉冲信号, 但是该系统对脉冲信号与噪声的强度要求相对比较高。该随机共振系统中双稳态的高阈值超过了1 MW/cm2, 即只有当噪声与脉冲信号叠加后的强度超过1 MW/cm2, 系统才可能产生随机共振现象, 这限制了该系统在微弱信号检测方面的应用。本节将用光子晶体替换反射镜, 以此构建阈值较低的随机共振系统。

2.1 光子晶体3D DSM法布里-珀罗腔

本节采用一对平面对称的一维光子晶体构建法布里-珀罗腔, 并将3D DSM置于腔的正中间, 如图 6所示。光子晶体由2种电介质A与B交替组成, 其周期为4, 介质A和B的厚度分别为da=λ/4na, db=λ/4nb。其中λ=300 μm为入射光波长, 入射角θ=0。介质A为聚甲基戊烯(TPX), 其折射率na=1.46;介质B为SiO2, 其折射率nb=1.9。3D DSM的厚度为dDSM=20 nm, 法布里-珀罗腔的腔长为L=300 μm, 并且腔的中间填充空气。将3D DSM置于腔的正中间, 即L=2L1=2L2。

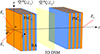thumbnail 图6

含有3D DSM/PhC的法布里-珀罗腔示意图

本节仍然采用传输矩阵的形式描述该系统, 其传输矩阵如(15)式所示。

式中，MA和MB分别为单层介质A和介质B的传输矩阵, 其表达式为

计算后可得到光腔入射光强与出射光强的双稳态表达式为

式中：t1, r1是PhC1的等效透射系数与等效反射系数；t2, r2是PhC2的等效透射系数与等效反射系数。

同样地，计算了光子晶体法布里-珀罗腔中不同费米能量与弛豫时间下的双稳态关系, 如图 7所示。图 7a)中的弛豫时间τ=1.0 ps, 图 7b)中的费米能量EF=0.2 eV。从图 7中可以看出, 随着费米能量的增加, 双稳态区间也增加; 而随着弛豫时间的增加双稳态区间减小。这与图 2中双稳态关系的变化趋势相似, 但与之不同的是此处双稳态的高低阈值远小于图 2中双稳态的高低阈值。以图 7a)中费米能量EF=0.2 eV曲线为例, 双稳态曲线对应的低阈值和高阈值为87 kW/cm2和145 kW/cm2, 相比图 7a)中EF=0.2 eV曲线对应的低阈值0.89 MW/cm2和高阈值1.36 MW/cm2降低了一个数量级。

thumbnail 图7

光子晶体光腔中的双稳态关系

2.2 光子晶体3D DSM法布里-珀罗腔随机共振系统

使用基于光子晶体3D DSM法布里-珀罗腔构建随机共振系统, 如图 8所示。双稳态系统的参数被设置为T=300 K, EF=0.2 eV, τ=1.0 ps。同样使用加入了加性高斯白噪声的脉冲信号作为输入信号S(t)=S0·e-2(t/t0)2+N(t), 脉冲宽度同样设置为5 ns, 但输入脉冲信号S0的强度与之前不同, 这里固定为60 kW/cm2。

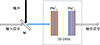thumbnail 图8

基于光子晶体3D DSM法布里-珀罗腔的随机共振系统

图 9显示了该随机共振系统中不同噪声下的输入信号以及对应重构后的输出信号。与图 4类似, 图 9a)~9d)中分别对应0, 60, 80, 100 kW/cm2的噪声强度, 图 9e)~9h)描绘了对应重构后的输出信号。图 9e)给出了无噪声强度下的输出信号, 图 9f)~9h)分别给出了欠共振状态与过共振状态的随机共振系统。而图 9g)中, 当噪声强度为80 kW/cm2时, 所有脉冲在噪声的帮助下跳转至高输出模式并与输入脉冲同步, 此时该系统可以有效地重构脉冲信号。

thumbnail 图9

不同噪声强度下的输入信号及对应的输出信号(脉冲信号强度60 kW/cm2, 噪声强度0~100 kW/cm2)

对比图 9e)~9h)和图 4e)~4h), 随着噪声强度的逐渐增加, 2个随机共振系统都先后经历了欠共振、共振以及过共振状态, 在共振状态下2个随机共振系统的输出信号都得到了有效重构。图 4对应图 3的随机共振系统, 其中信号强度为0.4 MW/cm2, 噪声强度在0~1.0 MW/cm2之间变化。图 9对应图 8的随机共振系统, 其中信号强度为60 kW/cm2, 噪声强度在0~100 kW/cm2之间变化。可以看出, 图 8的随机共振系统对信号强度以及噪声强度的需求远小于图 3的随机共振系统。

最后计算了该随机共振系统不同噪声强度下的互相关系数与互相关增益, 如图 10所示。可以看出最高互相关增益约为3, 与图 5中的最高互相关增益3.2相近。由此可以看出, 使用了光子晶体替换反射镜可以有效降低随机共振系统的阈值, 降低其对噪声及信号强度的需求, 且不会对随机共振系统的信号重构性能产生影响。

thumbnail 图10

光子晶体光腔随机共振系统中噪声强度与互相关系数及互相关增益的关系

3 结论

本文设计了2种基于3D DSM法布里-珀罗腔的随机共振系统, 分析了不同参数对随机共振系统中双稳态的影响, 并用这2种随机共振系统对含噪脉冲信号进行重构。为了评估它们的信号重构性能, 计算了随机共振系统中原始输入信号、输入信号与输出信号之间的互相关系数与互相关增益。结果表明, 2种随机共振系统的最大互相关增益分别达到了3.2和3, 均可有效重构含噪脉冲信号。通过数据对比得知, 使用光子晶体光腔的随机共振系统阈值远低于使用反射镜光腔的随机共振系统, 可以对强度相对较低的含噪脉冲信号进行重构。这为微弱脉冲信号的检测提供了一种有效方法。

References

  1. YANG Dingxin. Stochastic resonance method for weak feature signal detection and application research[D]. Changsha: National University of Defense Technology, 2004 (in Chinese) [Google Scholar]
  2. BENZI R, PARISI G, STERA A, et al. Stochastic resonance in climatic change[J]. Tellus, 1982, 34(1): 10–16 [Google Scholar]
  3. BEZRUKOV S M, VODYANOY I. Stochastic resonance in non-dynamical systems without response thresholds[J]. Nature, 1997, 385(6614): 319 [Google Scholar]
  4. KISS L B, GINGL Z, MÁRTON Z, et al. 1/f noise in systems showing stochastic resonance[J]. Journal of Statistical Physics, 1993, 70(1): 451–462 [Google Scholar]
  5. DONNELLY C, TAN D T H. Ultra-large nonlinear parameter in graphene-silicon waveguide structures[J]. Optics Express, 2014, 22: 22820–22830 [Google Scholar]
  6. GULLANS M, CHANG D E, KOPPENS F H L, et al. Single-photon nonlinear optics with graphene plasmons[J]. Physical Review Letters, 2013, 111: 247401 [Google Scholar]
  7. JIANG T, KRAVTSOV V, TOKMAN M, et al. Nonlinear nanoimaging of ultrafast coherent dynamics of graphene[C]//Conference on Lasers and Electro-Optics, 2019: 838–843 [Google Scholar]
  8. LONG X, BAO Y W. Low threshold optical bistability based on topological edge state in photonic crystal heterostructure with Dirac semimetal[J]. Optics Express, 2022, 30: 20847–20858 [Google Scholar]
  9. WANG Z, WENG H, WU Q, et al. Three-dimensional Dirac semimetal and quantum transport in Cd3As2[J]. American Physical Society, 2013, 88: 125427 [Google Scholar]
  10. WAN X, TURNER A M, VISHWANATH A, et al. Topological semimetal and fermi-arc surface states in the electronic structure of pyrochlore iridates[J]. Physical Review, 2011, 83: 205101 [Google Scholar]
  11. ORLITA M, BASKO D M, ZHOLUDEV M S, et al. Observation of three-dimensional massless Kane fermions in a zinc-blende crystal[J]. Nature Physics, 2014, 10: 233–238 [Google Scholar]
  12. YOUNG S, ZAHEER S, TEO J, et al. Dirac semimetal in three dimensions[J]. Physical Review Letters, 2012, 108: 140405 [Google Scholar]
  13. WANG Z, SUN Y, CHEN X, et al. Dirac semimetal and topological phase transitions in A3Bi(A=Na, K, Rb)[J]. Physical Review B, 2012, 85: 195320 [Google Scholar]
  14. OOI K J A, ANG Y S, ZHAI Q, et al. Nonlinear plasmonics of three-dimensional Dirac semimetals[J]. APL Photonics, 2019, 4: 034402 [Google Scholar]
  15. LIANG T, GIBSON Q, ALI M N, et al. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2[J]. Nature Materials, 2015, 14: 280–284 [Google Scholar]
  16. VELDHORST M, SNELDER M, HOEK M, et al. Josephson supercurrent through a topological insulator surface state[J]. Nature Materials, 2012, 11: 417–421 [Google Scholar]
  17. NEUPANE M, XU S Y, SANKAR R, et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2[J]. Nature Communications, 2014, 5: 3786 [Google Scholar]
  18. HE L P, HONG X C, DONG J K, et al. Quantum transport evidence for the three-dimensional Dirac semimetal phase in Cd3As2[J]. Physical Review Letters, 2014, 113: 246402 [Google Scholar]
  19. POLITANO A, CHIARELLO G, GHOSH B, et al. 3D Dirac plasmons in the type-Ⅱ Dirac semimetal PtTe2[J]. Physical Review Letters, 2018, 121: 086804 [Google Scholar]
  20. LIU Z K, ZHOU B, ZHANG Y, et al. Discovery of a three-dimensional topological Dirac semimetal Na3Bi[J]. Science, 2014, 343: 864–867 [CrossRef] [Google Scholar]
  21. CHEN R Y, ZHANG S J, SCHNEELOCH J A, et al. Optical spectroscopy study of the three-dimensional Dirac semimetal ZrTe5[J]. Physical Review B, 2015, 92: 075107 [Google Scholar]
  22. LI C, HU X, YANG H, et al. Unidirectional transmission in 1D nonlinear photonic crystal based on topological phase reversal by optical nonlinearity[J]. AIP Advances, 2017, 7(2): 025203 [Google Scholar]
  23. POSHAKINSKIY A V, PODDUBNY A N, PILOZZI L, et al. Radiative topological states in resonant photonic crystals[J]. Physical Review Letters, 2014, 112(10): 107403 [Google Scholar]
  24. LU Ling, FANG Chen, FU Liang, et al. Symmetry-protected topological photonic crystal in three dimensions[J]. Nature Physics, 2016, 12(4): 337 [Google Scholar]
  25. VERBIN M, ZILBERBERG O, KRAUS Y E, et al. Observation of topological phase transitions in photonic quasicrystals[J]. Physical Review Letters, 2012, 110(7): 076403 [Google Scholar]
  26. GAO W, LAWRENCE M, YANG B, et al. Topological photonic phase in chiral hyperbolic metamaterials[J]. Physical Review Letters, 2015, 114(3): 037402 [Google Scholar]
  27. HAFEZI M, MITTAL S, FAN J, et al. Imaging topological edge states in silicon photonics[J]. Nature Photonics, 2013, 7(12): 1001–1005 [Google Scholar]
  28. GAO W, HU X Y, LI C, et al. Fano-resonance in one-dimensional topological photonic crystal heterostructure[J]. Optics Express, 2018, 26(7): 8634–8644 [Google Scholar]
  29. LEYONG J, JUN G, LEIMING W, et al. Manipulating the optical bistability at terahertz frequency in the Fabry-Perot cavity with graphene[J]. Optics Express, 2015, 23: 31181–31191 [Google Scholar]
  30. WANG T, CAO M, ZHANG Y, et al. Tunable polarization-nonsensitive electromagnetically induced transparency in Dirac semimetal metamaterial at terahertz frequencies[J]. Optical Materials Express, 2019, 9: 1562–1576 [Google Scholar]
  31. BARTUSSEK R, HÄNGGI P, JUNG P. Stochastic resonance in optical bistable systems[J]. Physical Review E, 1994, 49(5): 3930 [Google Scholar]
  32. BONIFACIO R, MEYSTRE P. Critical slowing down in optical bistability[J]. Optics Communications, 1979, 29(1): 131–134 [Google Scholar]
  33. WANG Q, LI C Z, GE S , et al. Ultrafast broadband photodetectors based on three-dimensional dirac semimetal Cd3As2[J]. Nano Letters, 2017, 17: 834–841 [Google Scholar]
  34. COLLINS J, CHOW C, IMHOFF T. Aperiodic stochastic resonance in excitable systems[J]. Physical Review E, 1995, 52(4): R332 [Google Scholar]

All Figures

thumbnail 图1

含有3D DSM的法布里-珀罗腔示意图
In the text
thumbnail 图2

反射镜光腔中的双稳态关系
In the text
thumbnail 图3

基于反射镜3D DSM法布里-珀罗腔的随机共振系统
In the text
thumbnail 图4

不同噪声强度下的输入信号及对应的输出信号(脉冲信号强度0.4 MW/cm2, 噪声强度0~1.0 MW/cm2)
In the text
thumbnail 图5

反射镜光腔随机共振系统中噪声强度与互相关系数及互相关增益的关系
In the text
thumbnail 图6

含有3D DSM/PhC的法布里-珀罗腔示意图
In the text
thumbnail 图7

光子晶体光腔中的双稳态关系
In the text
thumbnail 图8

基于光子晶体3D DSM法布里-珀罗腔的随机共振系统
In the text
thumbnail 图9

不同噪声强度下的输入信号及对应的输出信号(脉冲信号强度60 kW/cm2, 噪声强度0~100 kW/cm2)
In the text
thumbnail 图10

光子晶体光腔随机共振系统中噪声强度与互相关系数及互相关增益的关系
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.