| Issue |
JNWPU
Volume 37, Number 3, June 2019
|
|
|---|---|---|
| Page(s) | 457 - 464 | |
| DOI | https://doi.org/10.1051/jnwpu/20193730457 | |
| Published online | 20 September 2019 | |
Study on Infrared Air-to-Air Missile Guidance Accuracy Affected by Complicated Environment
复杂环境对红外空空导弹制导精度影响规律研究
1
School of Astronautics, Northwestern Polytechnical University, Xi’an, 710072, China
2
School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, 710072, China
Received:
27
May
2018
The guidance accuracy of an infrared air-to-air missile is affected by various factors such as target maneuver, interference, and the natural environment. The complicated confrontational environment posed by target maneuver and decoy launch is considered in this article. The more practical adjoint analysis model for the influence of target maneuver and decoy launch on missile guidance accuracy is established by analyzing the jamming process, motion characteristics, and the influence mechanism on the guidance system of point source decoy. By using the adjoint method, the barrel roll maneuver angular rate, the numble of simultaneous decoy launch, the ignition time, the interval between launches and the strategy influence on the miss distance of the missile are analyzed in detail, which will provide strategic references for the aircraft to fight against the infrared air-to-air missiles.
摘要
红外空空导弹制导精度受目标机动、干扰以及自然环境等多种因素影响。考虑目标机动和投放诱饵弹所构成的复杂对抗环境，通过分析点源诱饵弹干扰过程、运动特性以及对制导系统的作用机理，建立了更符合实际情况的目标机动和诱饵投放对导弹制导精度影响的伴随分析模型。利用伴随法，分析了目标机桶滚角速率以及诱饵弹的齐投数量、起燃时间、投放间隔与策略对导弹脱靶量的影响规律，为战斗机采取对抗红外空空导弹策略提供参考。
Key words: barrel roll maneuver / decoy launch / strategy / infrared guided missile / guidance accuracy / miss distance / adjoint analysis model
关键字 : 桶滚机动 / 诱饵投放 / 策略 / 红外制导导弹 / 制导精度 / 脱靶量 / 伴随分析模型
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
红外空空导弹是最有效的近距空战杀伤武器，并有数据显示，半数的飞机在空战中都是由红外空空导弹击落，这个比例正在不断提高[1]。因此，研究针对红外空空导弹的对抗策略，是十分有必要的。Timo等[2]建立了目标桶滚机动的简易模型并利用伴随法对其合理性进行了验证，Imado等[3]在目标桶滚机动对导弹脱靶量影响方面进行了研究，但上述研究都未考虑诱饵影响。Arthur等[4]利用伴随法[5]研究了目标机动和诱饵干扰对导弹脱靶量的影响，从而给出了相应的对抗策略，但其研究的是平面机动，且未考虑诱饵弹受力影响。黄鹤松等[6]基于真实数据建立了目标机动及面源诱饵的运动和辐射模型，并针对前向来袭导弹结合目标机动和诱饵投放进行了策略分析，但其对多诱饵的投放策略等研究较少。本文建立了红外诱饵弹运动模型，并考虑诱饵弹压制比差异，建立了红外诱饵弹在干扰过程中的能量中心变化模型，然后研究了在空间中目标桶滚机动和诱饵投放对抗红外导弹的战术策略。
1 诱饵作用过程描述及建模
根据红外诱饵弹的辐射特性可将其分为点源诱饵弹和面源诱饵弹[7]。本文针对点源诱饵进行建模仿真。
分析导弹对抗诱饵的过程，战机投放诱饵弹至起燃时间[8]，在导弹导引头视场内生成与目标红外特性相近的辐射源，此时诱饵弹已脱离战机一段距离，导引头在一段时间内无法分辨真实目标与诱饵，不失一般性，假设当导弹受到诱饵干扰时，视线指向目标与导弹的能量中心，即质心干扰原理[9]。通常红外诱饵弹投放技术参数有起燃时间、持续燃烧时间、齐投数量、组投放间隔、投射方向策略等。导弹抗干扰的过程可描述为4个阶段[4, 10]，如图 1所示。
导弹末制导锁定目标, 此时载机导弹告警系统发出告警信号, 在ta时刻发射诱饵, 此时诱饵脱离战机, 但尚未起燃, 如图 1a)所示。tb时刻诱饵弹燃烧后, 由于导弹导引头无法瞬时分辨诱饵和目标, 导引头将跟踪诱饵和目标的能量中心, 即“假目标”, 能量中心位移、速度和加速度均会发生跳变, 即目标视线角发生“突跳”, 如图 1b)所示。且随着诱饵和战机的运动, “假目标”将按照一定的速度和加速度远离战机, 且诱使导引头锁定“假目标”运动, 如图 1c)所示。当经过时间间隔tbc后, 即在tc时刻导引头通过抗干扰算法已成功分离诱饵和目标, 导弹重新锁定目标(假定目标未出导引头视场, 若此时目标已出视场, 则导引头丢失目标, 不在本文讨论之列), 目标视线角发生“突跳”, 如图 1d)所示。图中VM, VT分别为导弹和目标的速度, Vc=VM+VT为弹目接近速度。为简单起见, 令初始目标视线角λ=0, 弹目距离R=Vctgo, 其中tgo=tF-t为剩余飞行时间, t为飞行时间, tF为遭遇点时刻, tF对应的弹目距离即为脱靶量。nM, nT分别为导弹和目标机动过载。VD为诱饵速度, yC, VCy, aCy为能量中心Y方向即铅锤方向运动距离、运动速度以及加速度, 并用Z方向代表水平方向。ΔyCb, ΔVCb, ΔaCb分别为诱饵弹起燃时能量中心位移、速度和加速度跳变值, ΔyCc, ΔVCc, ΔaCc分别为导弹重新锁定目标后能量中心位移、速度和加速度跳变值。
为了有效地诱偏红外制导空空导弹, 红外诱饵弹的辐射强度总是设计得比载机的红外辐射强度大, 动态时诱饵辐射能量与目标辐射能量比值即压制系数K一般在2~3之间[11]。可认为目标一次齐投诱饵弹所形成的红外辐射源强度为单个诱饵弹辐射强度之和[9], 根据质心干扰原理, 假设目标机动和诱饵运动都在铅垂平面进行, 则Y方向能量中心可由(1)式求出, Z方向与Y方向类似。
式中, WD表示单个诱饵的辐射强度, WT表示目标的辐射强度, yT, VDy, aDy分别为诱饵弹Y方向的位移、速度和加速度, yT, VTy, aTy分别为战机Y方向的位移、速度和加速度, n为诱饵弹一次齐投数目。
 |
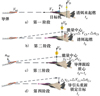图1 空空导弹与抗干扰过程 |
2 诱饵投放和目标机动对导弹干扰伴随模型
2.1 红外诱饵弹模型
诱饵弹在发射后主要受到重力和空气阻力的作用。其运动方程如下
式中, f为诱饵弹所受阻力, Cd为阻力系数, S为诱饵弹的迎风面积, ρ为大气密度, mD为诱饵弹质量, VDx, VDy, VDz为导弹速度在地面系的分速度, g为重力加速度。
诱饵弹初速度计算可参考文献[12], 本文讨论桶滚机动中诱饵弹的初速度VDx0, VDy0, VDz0可通过(3)式进行计算
式中, VF为诱饵弹相对目标机发射速度, 向桶滚机动外侧投射时为正, 反之为负。ϕ为投射诱饵时目标桶滚机动方位角。
以Y方向为例, 建立诱饵弹模型, Z方向与此类似。为了方便建模, 认为在导弹识别真实目标阶段, 诱饵弹加速度aDy为常值, 其具体计算如下
式中, VDyb为导弹跟踪质心起始tb时诱饵弹Y向速度, VDyc为导弹识别出目标时刻tc时诱饵弹Y向速度, tbc=tc-tb为诱饵弹诱偏作用时间, 即导引头抗干扰算法识别出真实目标时间。当目标无机动, 根据上述讨论可知, 诱饵的干扰过程如图 2所示。图 2中诱饵在ta时刻发射, 至tb时刻起燃, tc时刻被导引头抗干扰算法剔除。yDb, yDc分别表示tb, tc时刻诱饵弹相对ta时刻的位移量, 目标tb, tc时刻位移yTb, yTc定义与之类似。在第一阶段(ta~tb), 诱饵弹发射但尚未达到有效辐射强度, 诱饵弹对导引头视线角并未产生影响, 则此阶段诱饵弹引起的质心加速度、速度和位移均未发生变化; 在第二阶段(tb), 诱饵弹燃烧后, 此时导引头跟踪对象不再是真实目标, 而是诱饵与真实目标的能量中心/质心, 此时诱饵弹已经脱离目标一段距离, 质心加速度、速度和位移均发生跳变, tb时刻由诱饵弹引起的质心加速度跳变量ΔaDyb、速度跳变量ΔVDyb和位移跳变量ΔyDb可通过公式(5)计算; 第三阶段(tb~tc), 由于之前已经认为诱饵弹引起的质心加速度为常值, 则速度线性变化, 位移呈抛物线型变化; 第四阶段, 导引头成功分辨诱饵与真实目标, 其跟踪对象从能量中心跳变回真实目标, tc时刻由诱饵弹引起的质心加速度跳变量ΔaDyc、速度跳变量ΔVDyc和位移跳变量ΔyDc及tb时刻跳变量可表示为
诱饵干扰作用下能量中心的线性模型可以图 3所示采用脉冲函数的形式给出, 图中VCD表示由诱饵投放对质心速度的影响量。
 |
图2 诱饵干扰过程 |
 |
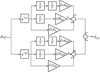图3 诱饵干扰作用下能量中心运动模型 |
2.2 目标机动模型
文献[2]所述模型考虑到战机桶滚机动时具备一定的法向初速度, 但是通常的情况是战机处于匀速巡航状态, 即假定在导弹发射时目标处于匀速直线飞行状态, 在导弹发射后目标先以额定过载能力做阶跃形式的过渡机动, 具备桶滚机动初速条件时, 实施桶滚机动, 该机动可以描述为战斗机在桶滚横截面做圆周运动, 在X方向上作匀速直线运动。
假设桶滚机动起始相位角为ϕ0, 目标额定过载能力为nT, 桶滚机动角速度为ω, 则目标桶滚机动初速VR=nTg/ω, 阶跃机动时间tstep=VR/(nTg)=1/ω, 目标Y方向和Z方向的过载值为nTy, nTz, 加速度值为aTy, aTz, 则目标阶跃机动时其值如(6)式所示。
则可以将目标机动形式转化为脉冲输入函数, 纵向加速度信号如图 4所示。
分析图 3所示红外空空导弹抗干扰过程, 在不存在速度指向偏差和初始位移偏差情况下, 桶滚机动对导弹脱靶量影响的模型如图 5所示:
图 5中, VCT表示投射诱饵时由目标机动对质心速度的影响量。根据公式(1)在诱饵开始工作即tb时刻, 目标对质心加速度的影响减小KD倍, 在诱饵停止工作即tc时刻目标对质心加速度的影响又增大KD倍。ΔVTyb, ΔyTb为tb时刻由于诱饵开始工作后目标使质心产生的速度和位移跳变值, ΔVTyc, ΔyTc为tc时刻由于诱饵停止工作后目标使质心产生的速度和位移跳变值。aTyb, aTyc分别为tb, tc时刻加速度跳变的输入量, 为了确保在加速度跳变时刻与aTy相位的一致性, 需对正弦信号初始相位按照公式(7)进行调整, 图 5所示为其转化为脉冲输入的形式。
跳变量ΔVTyb, ΔyTb可由ta~tb时间段真实目标与质心的初始位置差、初始速度差以及加速度差获得, 同理可计算ΔVTyc, ΔyTc, 计算过程可由公式(8)表示, 公式中t < tb和t < tc表示在未到达tb和tc时刻速度和位移不发生跳变, 即跳变量为零。
式中, VTya, VTyb分别表示ta和tb时刻目标的速度。在MATLAB仿真中通过积分、Enabled和Triggered等模块可完成仿真模型的建立。运用该方法可以避免复杂的分情况讨论以及参数推导, 同时可以完成对更复杂机动方式和连续机动以及多诱饵投放的研究。
 |
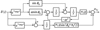图4 脉冲输入的纵向加速度信号 |
 |
图5 桶滚机动作用下能量中心运动模型 |
2.3 伴随分析模型的建立
经过上述讨论, 以Y方向为例, 结合图 3所示VCD和图 5所示VCT计算模块, 建立一次诱饵投放过程中目标桶滚机动对导弹干扰线性化模型, 如图 6所示。
图 6中模型参数[2]τSH表示导弹导引头时间常数, τN表示信号处理时间常数, τAP表示导弹自动驾驶仪时间常数, ωM表示导弹气动响应角频率, ζ表示导弹阻尼比, N为比例导引系数，aMy为导弹y方向实际加速度值。
按照线性系统伴随模型的建立准则[5, 10], 可建立目标桶滚机动和诱饵投放对导弹干扰伴随分析模型。图 6所示模型有3个输入，则导弹y方向脱靶量my可由伴随模型3个输出之和得到。同理可以建立z方向导弹脱靶量mz, 则导弹总脱靶量mall计算公式为[13]
对于多诱饵情况, 只需在导弹伴随分析模型外并联相应时间的跳变量计算模块即可, 同时应用伴随法, 可通过一次伴随仿真得到直接法需多次仿真才能计算的结果, 计算效率显著提高。
 |
图6 导弹受目标机动和诱饵投放干扰线性化模型 |
3 仿真与分析
3.1 目标桶滚机动与诱饵投放仿真结果
目标做桶滚机动过程中投放诱饵, 某典型诱饵弹初始质量为0.25 kg, 质量消耗率为0.03 kg/s, 迎风面积S为0.003 2 m2, 燃烧时间为4 s, 发射速度VF为30 m/s, 发射角为90°, 取起燃时间为0 s, Cd=0.3, 发射时战机飞行高度为3 km, 过载为6g, 速度为0.8Ma, 桶滚角速率为2 rad/s, 则可求得诱饵弹在地面系的速度, 诱饵弹在地面系位移量可通过对速度积分求得, 在目标机桶滚相位角分别为0°, 60°, 120°, 180°, 240°, 300°时投射诱饵弹, 其OYZ平面轨迹图及速度随时间变化情况如图 7所示。
诱饵弹投放组间隔应不小于tbc, 因为如果在前一组诱饵尚未移出导弹视场或目标尚未被导弹识别之前投放下一组诱饵, 会影响前一组诱饵形成的质心干扰, 使质心向目标方向移动[4]。实际作战中, 作战态势、诱饵弹的齐投数量、方向、速度等都会造成导引头识别真实目标时间的差异, 为进行规律分析此处认为导引头识别真实目标时间不发生变化, 本文取tbc=0.5 s。通过计算可得不同桶滚机动起始相位角时诱饵弹各时刻位移、速度和加速度值。
 |
图7 诱饵投放轨迹及速度变化曲线 |
3.2 桶滚机动对导弹脱靶量影响分析
仿真条件:取最大剩余飞行时间tmax=6 s, τSH=0.1 s, τN=0.11 s, τAP=0.15 s, ωM=18 rad/s, ζ=0.7, N=4, Vc=1 500 m/s, ϕ0=0°, ω选为1 rad/s, 1.5 rad/s, 2 rad/s, 3 rad/s, 4 rad/s, 导弹尾后追击目标机, 其余仿真参数设置同图 7, 研究桶滚机动角速率对导弹脱靶量影响。导弹脱靶量随剩余飞行时间变化情况如图 8所示。
从图 8中可以看出, 该仿真条件下, 当剩余飞行时间大于2.5 s, 桶滚角速率在2~3 rad/s时产生的脱靶量最大, 均大于25 m, 所以要使导弹产生足够大的脱靶量, 战机必须具备充裕的时间进行桶滚机动, 战机应尽量将导弹置于尾后以消耗导弹能量并增加剩余飞行时间。
 |
图8 各桶滚角速率值对应脱靶量随tgo变化曲线 |
3.3 桶滚机动时诱饵投放对导弹脱靶量影响分析
3.3.1 诱饵弹齐投数量、投放组间隔对导弹脱靶量影响
红外诱饵弹参数设置同图 7, 相对目标机身垂直向下投射, 投放组间隔为0.7 s, 目标桶滚机动角速率为2 rad/s, 其余参数与图 8相同。投射1枚诱饵的压制比K=2, 则齐投n枚时K=2n, 齐投数量对导弹脱靶量影响如图 9所示, 图中K=0表示目标只做桶滚机动不投放诱饵。
为方便进行比较分析, 引入平均脱靶量m如(10)式所示。
式中，m(tgo)表示伴随模型所得tgo对应的导弹脱靶量。诱饵弹投放组间隔从0.5~4.1 s间隔0.2 s变化, 则得导弹平均脱靶量随投放组间隔变化如图 10所示。
从图 9可以看出, 在该投放组间隔下，导弹脱靶量存在多个极值和极小值，投诱饵比不投诱饵能产生更大的脱靶量，齐投数量越多，脱靶量越大。同时, 从图 10可得齐投数量越多, 投放组间隔越小, 导弹平均脱靶量越大, 投诱饵比不投诱饵能产生更大的平均脱靶量, 但是随着齐投数量的增大, 平均脱靶量增长幅度越来越小, 因为战斗机携带诱饵弹数量有限, 并且一般要对抗多次导弹来袭, 则在该仿真条件下, 诱饵弹齐投数量在2或3, 投放间隔小于1 s为宜。
 |
图9 不同K时导弹脱靶量随tgo变化曲线 |
 |
图10 不同K时导弹平均脱靶量随投放组间隔变化曲线 |
3.3.2 起燃时间、投放策略对导弹脱靶量影响
诱饵投放策略选为“向外”、“向内”、“外内外”和“内外内”4种, 其具体投放方式如图 11所示。
图 11中圆表示桶滚机动横截面, “内”和“外”指诱饵投射是朝圆周运动的内侧或外侧投射, 假设桶滚一周投射8组诱饵, 投射速度依次为VD1~VD8, 其大小相同但方向不同。选取仿真条件如下:桶滚机动起始相位角为0°, 齐投数量为2, 投放组间隔为0.7 s, 起燃时间从0~0.6 s间隔0.1 s变化, 其余仿真条件不变, 则导弹平均脱靶量变化如图 12所示。
从图 12可以得出，在相同起燃时间情况下，采用向外投放策略，会使导弹平均脱靶量达到最大，向内投放策略平均脱靶量最小，其余2种投放策略介于两者之间。所有投放策略的平均脱靶量随起燃时间的增加而增大，但导弹导引头视场角很小，起燃时间过长会使诱饵弹起燃时距离目标过远甚至已出视场从而起不到干扰作用。所以，桶滚机动中应选取向外投射诱饵策略，同时起燃时间应适中。
 |
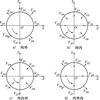图11 4种诱饵弹投放策略 |
 |
图12 不同投放策略下导弹平均脱靶量随起燃时间变化曲线 |
4 结论
文中建立了更为实际的目标桶滚机动模型、诱饵投放模型和对导弹制导精度的伴随分析模型，研究了目标桶滚机动和红外诱饵弹对红外制导导弹脱靶量影响。在导弹告警系统发出告警信号后，目标机应将导弹置于尾后，阶跃机动达到速度条件后进行角速率为2~3 rad/s的桶滚机动，同时向桶滚机动横截面外侧即相对战机向下投放诱饵弹。典型条件下诱饵弹投放时组间率隔尽可能接近导引头识别时间，每组投放2或3枚诱饵，同时合理控制诱饵弹起燃时间。本研究对于目标机动逃逸及诱饵弹投放具有指导意义。
References
- HuangHesong, TongZhongxiang, LiJianxun, et al. Functional Simulation of Infrared Air-to-Air Missiles Based on Combat Assessment[J]. Infrared and Laser Engineering, 2015, 44(3): 803-809 [Article] [Google Scholar]
- Timo Sailaranta, Ari Siltavuori, Antti Pankkonen. Simple Missile Models against High-G Barrel Roll Maneuver[C]//AIAA Guidance, Navigation, and Control Conference, 2011: 08-11 [Google Scholar]
- FumiakiImado, SusumuMiwa. Missile Guidance Algorithm Against High-G Barrel Roll Maneuvers[J]. AIAA Journal of Guidance, Control and Dynamics, 1994, 17(4): 123-128 [Article] [CrossRef] [Google Scholar]
- Arthur Vermeulen, Gerrit Maes. Missile Avoidance Manoeuvres with Simultaneous Decoy Deployment[C]//AIAA Guidance, Navigation, and Control Conference, 2009: 10-13 [Google Scholar]
- PaulZarchan. Tactical and Strategic Missile Guidance[M]. 5th edition AIAA, Reston, Virginia, 2007 [Google Scholar]
- HuangHesong, TongZhongxiang, LiTaorui. Defense Strategy of Aircraft Confronted with IR Guided Missile[J]. Mathematical Problems in Engineering, 2017(7): 1-9 [Article] [Google Scholar]
- HanXiaona. The Research of Infrared Decoy Simulation[J]. Xi'an, Xidian University, 2015 [Google Scholar]
- WangChaoqun. Some Characteristics of Infrared Jam and Its Simulationtechnique on Infrared Guided Missile[J]. Inrared and Laser Engineering, 2001, 30(4): 163-167 (in Chinese) [Article] [Google Scholar]
- HuZhaohui,ChenKai, YanJie. Operational Parameters of Airborne Infrared Decoy Aerial-Lauched Set[J]. Inrared and Laser Engineering, 2008, 37(3): 396-399 [Article] [Google Scholar]
- PanXiangyu, JiXiaoliang, YuYunfeng, et al. Analysis of Jam Effect for Radar Decoy Against Air-to-Air Missile[J]. Command Control & Simulation, 2014, 36(2): 29-32 (in Chinese) [Article] [Google Scholar]
- HongYang, ZhangKe, LiYanjun. Simulation and Jamming Model of Infrared Bait[J]. Journal of System Simulation, 2006, 18(2): 463-466 [Article] [Google Scholar]
- WuXiaodi, HuangChaochao. Simulation for the Motion Traces of Infrared Decoys[J]. Laser & Infrared, 2015, 45(12): 1473-1476 (in Chinese) [Article] [Google Scholar]
- GuWenjin, BiLanjin, WUZhidong. Missile Distance Analysis of Terminal Maneuver Penetration for Surpersonic Anti-Ship Missile Based on Adjoint Technique[J]. Journal of Naval Aeronautical and Astronautical University, 2009, 24(4): 400-404 (in Chinese) [Article] [Google Scholar]
All Figures
|
图1 空空导弹与抗干扰过程 |
| In the text | |
|
图2 诱饵干扰过程 |
| In the text | |
|
图3 诱饵干扰作用下能量中心运动模型 |
| In the text | |
|
图4 脉冲输入的纵向加速度信号 |
| In the text | |
|
图5 桶滚机动作用下能量中心运动模型 |
| In the text | |
|
图6 导弹受目标机动和诱饵投放干扰线性化模型 |
| In the text | |
|
图7 诱饵投放轨迹及速度变化曲线 |
| In the text | |
|
图8 各桶滚角速率值对应脱靶量随tgo变化曲线 |
| In the text | |
|
图9 不同K时导弹脱靶量随tgo变化曲线 |
| In the text | |
|
图10 不同K时导弹平均脱靶量随投放组间隔变化曲线 |
| In the text | |
|
图11 4种诱饵弹投放策略 |
| In the text | |
|
图12 不同投放策略下导弹平均脱靶量随起燃时间变化曲线 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.