| Issue |
JNWPU
Volume 38, Number 3, June 2020
|
|
|---|---|---|
| Page(s) | 604 - 609 | |
| DOI | https://doi.org/10.1051/jnwpu/20203830604 | |
| Published online | 06 August 2020 | |
Estimation of Full Strap-down Rotating Bomb Guidance Information Based on Unscented Kalman Filter
基于无迹卡尔曼的全捷联旋转弹导引信息估计
1
System Engineering Institute of Sichuan Aerospace, Chengdu 610100, China
2
The Third Academy of China Aerospace Science&Industry Corporation, Beijing 100074, China
Received:
6
January
2019
In this paper, the full strap-down seeker of rotating bomb is taken as the research object, and the method of extracting the LOS (line-of-sight) angle and angular rate of the full strap-down seeker of the rotating bomb is studied. The structure of the full strap-down seeker is quite different from that of the conventional rate gyro seeker. The measurement system of full strap-down seeker is fixed to the missile, the seeker can only obtain the measurement information in the projectile coordinate system, and the measurement information is coupled with the body posture information, so it cannot be directly used for the control guidance of the rotating projectile. First, based on the conversion relationship between coordinate systems, the mathematical model of the inertial LOS angle of the rotating bomb is established, and the mathematical model of the extraction of the inertial LOS angle and angular rate of the rotating bomb is further established. Then, the Kalman filter is designed by using the unscented Kalman filter method (UKF), and the extracted LOS angle containing noise information is filtered. Finally, the mathematical simulation is carried out to verify the validity of the mathematical model of LOS angle and angular rate extraction. Compared with the Extended Kalman filter method (EKF), the UKF has a higher accuracy for estimating the navigation information of the full strap-down rotating projectile.
摘要
以旋转弹的全捷联导引头为研究对象,重点研究了旋转弹的全捷联导引头视线角及视线角速率估计方法。全捷联导引头的结构和传统速率陀螺导引头有较大差别,其测量系统与弹体固联,导引头只能获得弹体坐标系下的测量信息,并且测量信息中耦合有弹体姿态信息,无法直接用于旋转弹的控制制导。根据坐标系之间的转换关系建立了旋转弹惯性视线角的数学模型和视线角解耦模型,从而进一步确立旋转弹惯性视线角估计的数学模型。选用无迹卡尔曼滤波方法(UKF),设计出卡尔曼滤波器,对估计到的含有噪声信息的视线角进行滤波;最后进行数学仿真,验证了视线角估计数学模型的有效性,与扩展卡尔曼滤波方法(EKF)和容积卡尔曼滤波方法(CKF)相比,UKF对于全捷联旋转弹的导引信息估计有更高的精度。
Key words: rotating bomb / full strap-down seeker / inertial LOS angle / Kalman filter / simulation
关键字 : 旋转弹 / 全捷联导引头 / 惯性视线角 / 卡尔曼滤波 /
© 2019 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
旋转弹作为导弹家族中的一员, 具有系统结构简单、成本低、可靠性高等特点。其弹体的自旋运动会带来优势, 能够克服诸如推力偏心、起控点散布、弹体质量分布不均匀等问题[1]。随着导弹小型化和精准化的发展, 旋转弹有着广阔的发展前景。
本文研究的旋转弹所采用导引头为全捷联激光式导引头, 具有体积小、可靠性高、视线角速率不受限制及成本低等优点。国内外学者对导引信息估计方法进行了大量研究:邵真杰等[2]用无迹卡尔曼滤波方法解决了相控阵雷达导引头视线角重构的问题, 验证了无迹卡尔曼滤波方法在视线角估计方面的优越性; Jacques Waldman[3]设计了扩展卡尔曼滤波器, 估计出传统框架式导引头的弹目视线角速率; Dowan等[4]根据弹目视线角关系和坐标空间转换, 推导出弹目视线角速率和弹体姿态角及体视线角速率之间的关系, 从而实现对弹目视线角速率的估计; Wang等[5]重点研究了捷联导引头的2种弹目视线角速率估计方法, 一种是利用微分网络对弹目视线角进行微分以获得弹目视线角速率, 一种是利用卡尔曼滤波器来估计弹目视线角速率, 最后仿真证明了卡尔曼滤波器比网络微分法更具有优势。聂聪等[6]提出了一种基于中央差分卡尔曼滤波(CDKF)的视线角速率估计方法, 该方法充分利用了惯导系统角速率陀螺的信息, 简化了噪声模型, 避免了引入不可测的相对距离和相对速度信息, 比传统的卡尔曼滤波更能精确地估计视线角速率。贾鑫等[7]进行了全捷联导引头解耦技术的研究, 对多种具有代表性的解耦方案进行了分析, 认为卡尔曼滤波法估计视线角速率的效果较好。
全捷联式激光导引头的测量系统与旋转弹的弹体固联, 因而测量系统所测量出来的信息是弹体坐标系下的视线角信息, 不能直接用于旋转弹的控制制导[8]。旋转弹的控制制导需要惯性坐标系下的视线角信息, 因此需要解算出导引头在惯性系下的视线角信息, 并且过滤掉耦合在视线角信息中的噪声信号, 估计出有用的视线角信息。本文采用UKF方法进行了导引信息的估计, 并对比了UKF、EKF和CKF的滤波结果。本研究对于全捷联旋转弹的制导研究具有一定价值。
1 惯性视线角估计模型的建立
旋转弹全捷联导引头视线角信号估计会用到以下坐标系:地理坐标系(惯性坐标系)Oxyz, 弹体坐标系Oxbybzb, 视线坐标系Oxsyszs, 体视线坐标系Oxlylzl。用到的角度有俯仰角ϑ, 偏航角ψ, 滚转角γ, 视线方位角qy, 视线高低角qz, 体视线方位角qβ, 体视线高低角qα[9]。坐标系和角度的相关定义如下:
1) 地理坐标系Axyz
坐标系原点A取在导弹发射点上, Ax轴是弹道面与水平面交线, 指向目标方向为正; Ay轴与水平面垂直, 指向上方为正, Az轴与其他两轴构成右手坐标系。在文中, 将地理坐标系作为惯性坐标系使用。
2) 视线坐标系Oxsyszs
坐标系原点O取在导弹的瞬时质心, Oxs轴由导弹质心指向目标的质心; Ozs轴位于地理坐标系确定的水平面内, 与Oxs轴垂直; Oys轴与Oxs轴、Ozs轴互相垂直构成右手直角坐标系。
3) 体视线坐标系OxTyTzT
原点O取在导弹的瞬时质心上, OxT轴由导弹质心指向目标的质心, OyT轴位于弹体坐标系确定的Ox1z1平面内, 与OxT轴垂直。OzT轴与OxT, OyT轴互相垂直并构成右手直角坐标系。
视线方位角qλ:视线坐标系的Oxs轴在水平面内的投影和地理坐标系的Ax轴之间的夹角。
视线高低角qγ:视线坐标系的Oxs轴和水平面之间的夹角。
体视线高低角qα:导弹与目标连线(即图 2中的OxT轴)和弹体坐标系的Ox1z1平面之间的夹角。
体视线方位角qβ:导弹与目标连线在Ox1z1平面内的投影(即图 2中的Ox′轴)和弹体坐标系的Ox1轴之间的夹角。
全捷联激光导引头与旋转弹弹体固联, 其测量的体视线角信息耦合有惯性视线角信息和弹体姿态运动信息, 需要建立相应的解耦模型, 去掉耦合在测量信息中的弹体姿态运动信息[3, 10]。因此, 本文以含有噪声的体视线角信息qα和qβ作为观测量建立观测方程, 以制导需要的惯性视线角qy, qz和惯性视线角速率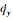 ,
, 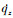 作为状态量建立状态方程, 从而完成惯性视线角估计数学模型的建立。
作为状态量建立状态方程, 从而完成惯性视线角估计数学模型的建立。
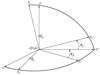 |
图1 地理坐标系与视线坐标系的角度 |
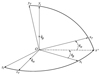 |
图2 弹体坐标系和体视线坐标系的角度 |
1.1 状态方程
将导弹和目标之间的距离定义为r, 则导弹接近目标的速度V可以表示为
式中:is, js, ks分别为视线坐标系Oxs轴,Oys轴和Ozs轴上的单位向量。视线坐标系相对地理坐标系的旋转角速度为
在视线坐标系中, 有
同理, 可以得到
将导弹和目标的相对速度进行微分后, 可得到弹目相对加速度为
如果目标是地面固定目标, 在短周期运动中, 弹目相对运动的速度矢量方向和大小变化不大, 则可以近似认为弹目相对加速度为0, 有
令状态方程的状态量为X=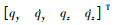 , 则状态方程为
, 则状态方程为
1.2 观测方程
目标在体视线坐标系和视线坐标系中的位置坐标均为[r 0 0]T, 根据坐标系之间的转换关系, 可以得到目标在弹体坐标系和地理坐标系中的坐标分别为
为了便于计算, 令坐标转换矩阵为
根据地理坐标系和弹体坐标系之间的转换关系可以得到
将(12)式进行解算, 可以得到观测方程为
2 卡尔曼滤波器的设计
全捷联激光导引头测量到的视线角信息中包含外界噪声和干扰信息, 如果将解耦得到的惯性视线角直接用于旋转弹的制导, 会导致导弹的制导精度较差, 甚至可能会使导弹脱靶。为了使导弹能够精准地命中目标, 需要进行滤波处理。从第1小节中的状态方程和观测方程可以看出, 惯性视线角估计模型的系统是非线性系统, 如果采用常规的滤波方法, 无法实现很好地滤波效果。旋转弹的导引信息估计属于一类强非线性条件的物理系统的滤波问题。无迹卡尔曼滤波方法放弃了对非线性系统进行线性化的传统方法, 而是在一步预测方程中, 利用无迹变换来处理均值和协方差的非线性传递, 因此不用忽略高阶项, 相较于EKF方法具有更好的精度。因此, 本文选择UKF作为滤波方法, 过滤掉视线角信息中的噪声和干扰, 估计出有用的视线角信息[11-13]。
2.1 无迹卡尔曼滤波算法的设计
对于本文建立的惯性视线角估计模型, 现写出无迹卡尔曼滤波算法设计步骤如下:
1) 选定滤波的初始状态值X0, Y0和协方差矩阵P0。
2) 计算出k-1时刻的sigma样本点集
3) 确定UT变换的权值系数
4) 根据算出来的sigma样本点, 计算k时刻的一步预测模型值
5) 计算k时刻的一步预测样本点
6) 计算方差矩阵P(XZ)k/k-1, P(ZZ)k/k-1
式中, 有
7) 计算滤波增益矩阵和滤波值更新
式中:α为很小的正数, 取值范围为10-4≤α≤1;β取值和状态量X的分布形式有关, 对于高斯正态分布的状态量, β=2为最优值。
3 仿真验证
根据第2小节设计的Kalman滤波器, 采用MATLAB编写程序, 进行仿真验证。本次数学仿真是针对带有目标位置装订误差和导航系统测量误差的情况, 在地理坐标系中, 实际目标的位置为(0, 2.5, 0)m, 目标位置坐标测量误差为(100, 50, 60)m, 因此, 弹载计算机利用导航信息进行制导指令解算时所采用的虚拟目标位置在地理坐标系中的坐标为(100, 52.5, 60)m。信号测量周期为50 ms。为了与UKF形成对比, 本文还进行了EKF和CKF(cubature Kalman filter容积卡尔曼滤波)的仿真, 并分析比较3种滤波方法的结果。仿真结果:
从以上结果可以看出, UKF、EKF和CKF滤波后的视线角信息和真实值非常接近, 可以应用于旋转弹的控制制导, 证明了本文提出的基于无迹卡尔曼滤波的视线角估计算法有效性。
从图 3、图 5和图 6可以看出, EKF在3种方法中的滤波误差最大。UKF相较于目前公认滤波效果较好的CKF方法, UKF在真实值附近的散布更小。在图 4中, CKF滤波值相较于UKF更接近真实值。综合图 3至6来看, UKF的滤波效果最好。
UKF、EKF和CKF滤波产生的滤波值与真实值误差均方根误差如表 1所示。
UKF、EKF和CKF滤波产生的滤波值与真实值误差均方根误差
从表 1来看, 单纯考虑UKF、EKF和CKF这3种滤波算法的解算误差, 三者对旋转弹的视线角速度估计效果比较接近。使用UKF所获得的滤波值, 其均方根误差均小于表 1中UKF、EKF和CKF滤波产生的滤波值与真实值误差均方根误差EKF和CKF滤波值, UKF算法的误差更小。但是由于UKF需要计算多个样本点, 所消耗的计算资源更大。
 |
图3 视线高低角滤波结果 |
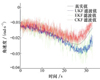 |
图4 视线高低角速度滤波结果 |
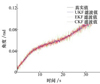 |
图5 视线方位角滤波结果 |
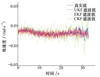 |
图6 视线方位角速度滤波结果 |
4 结论
本文介绍了基于无迹卡尔曼滤波的旋转弹视线角信息估计方法, 该方法能够解决视线角信息与弹体姿态信息的耦合问题, 以及旋转弹的自旋所造成的俯仰角和偏航角耦合问题, 并且采用无迹卡尔曼滤波方法估计出了有用的惯性视线角信息。仿真结果表明, 该方法估计出来的惯性视线角信息与真实值接近, 满足制导所需精度。从理论来看, UKF更适于解决非线性系统滤波问题。UKF未采用EKF对非线性函数进行线性化的方法, 以UT变换的方法来处理均值和协方差的非线性传递, 然后用确定性采样的方法来逼近状态的后验概率密度。因此, UKF没有忽略非线性函数的高阶项, 相较于EKF, UKF对于非线性系统的计算精度更高。相较于CKF, 主要区别在于样本点的计算方式不同, 当状态方程的维数较高时, CKF的滤波结果精度高于UKF。而在本文中, 明显可以看到UKF的滤波精度高于CKF, 计算时间也略低于CKF。因此, 在本文旋转弹视线角信息估计方面, UKF更适用。
References
- Sun Tingting. Research on Key Technology of Full Strapdown Guidance System[D]. Changchun: Graduate School of Chinese Academy of Sciences, 2016(in Chinese) [Google Scholar]
- Shao Zhenjie, Zhao Mingyuan. Line of Sight Reconstruction for Phased Array Radar Seeker[J]. Modern Defence Technology, 2015, 43 (6): 56– 60 [Article](in Chinese) [Google Scholar]
- Waldman Jacques. Line-of-Sight Rate Estimation and Linearizing Control of an Imaging Seeker in a Tactical Missile Guided by Proportional Navigation[J]. IEEE Trans on Control Systems Technology, 2002, 10 (4): 556– 567 [Article] [CrossRef] [Google Scholar]
- Kim Dowan, Ryoo Changkyung, Kim Yongho. Guidance and Control for Missiles with a Strapdown Seeker[C]//11th International Conference on Control, Automation and Systems, KINTEX, Gyeonggi-do, Korea, 2011: 969–972 [Google Scholar]
- Wang Wei, Lin Defu, Xu Ping. Strap-down Seeker LOS Angular Rate Estimation[J]. Infrared and Laser Engineering, 2015, 44 (10): 3066– 3069 [Article] [Google Scholar]
- Nie Cong, Zhang Ke. Line of Sight Angular Rate Estimation Algorithm for Strapdown Seeker[J]. Computer Simulation, 2017, 34 (1): 70– 73 [Article](in Chinese) [Google Scholar]
- Jia Xin, Luo Yanwei, Luo Li. Decoupling Technology of Full Strapdown Seeker[J]. Tactical Missile Technology, 2013 (1): 77– 81 [Article](in Chinese) [Google Scholar]
- Xiu Pengpeng, Li Xiaobing, Yang Yuzhe. A Method of Calculating the Line of Sight[J]. Photoelectric Engineering, 2012, 39 (7): 75– 80 [Article](in Chinese) [Google Scholar]
- Yuan Yifang. Research on Guidance and Control Technology of Full Strapdown Guided Ammunition[D]. Beijing: Beijing Institue of Technology, 2015(in Chinese) [Google Scholar]
- Li Jingjing. Research of LOS Rate Estimation Method for Strap-down Imaging Seeker[D]. Harbin: Harbin Institute of Technology, 2008(in Chinese) [Google Scholar]
- Sun T, Chu H, Zhang B, et al. Line-of-Sight Rate Estimation Based on UKF for Strapdown Seeker[J]. Mathematical Problems in Engineering, 2015 (1): 1– 14 [Article] [Google Scholar]
- Qin Yongyuan, Zhang Hongyue, Wang Shuhua. Kalman Filtering and Combined Navigation Principle[M]. Xi'an: Northwestern Polytechnical University Press, 2012 (in Chinese) [Google Scholar]
- Wang P, ZHANG K. Research on Line-of-Sight Rate Extraction of Strapdown Seeker[C]//Chinese Control Conference, 2014 [Google Scholar]
All Tables
All Figures
 |
图1 地理坐标系与视线坐标系的角度 |
| In the text | |
 |
图2 弹体坐标系和体视线坐标系的角度 |
| In the text | |
 |
图3 视线高低角滤波结果 |
| In the text | |
 |
图4 视线高低角速度滤波结果 |
| In the text | |
 |
图5 视线方位角滤波结果 |
| In the text | |
 |
图6 视线方位角速度滤波结果 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


