| Issue |
JNWPU
Volume 39, Number 2, April 2021
|
|
|---|---|---|
| Page(s) | 367 - 374 | |
| DOI | https://doi.org/10.1051/jnwpu/20213920367 | |
| Published online | 09 June 2021 | |
Exploring UAV's multi-domain joint anti-jamming intelligent decision algorithm
无人机多域联合抗干扰智能决策算法研究
1
College of Information and Navigation, Air Force Engineering University, Xi'an 710077, China
2
Key Laboratory of Aerospace Information Applications, China Electronics Technology Group, Shijiazhuang 050081, China
Received:
29
July
2020
To understand the complex communication environment of a UAV in battlefield, its unknown channel statistics information and poor intelligent jamming and anti-jamming capability, the multi-domain anti-jamming problem is studied, and a multi-domain joint anti-jamming intelligent decision algorithm is proposed. First, the channel selection method is adopted to deal with jamming in the frequency domain. A multi-arm slot machine's channel selection model is established, and the channel interference level is judged. Secondly, the moderate interference channel is suppressed in the power domain, and the model of its Stackelberg game is established. The game equalization is solved to obtain the best transmission power and reduce the overhead caused by channel switching. The simulation results show that the long-term rewards of the intelligent decision algorithm are significantly higher than those of the traditional multi-arm slot machine's algorithm and the random selection algorithm and that the average throughput of the communication system of the UAV is improved, thus proving the superiority of the intelligent decision algorithm.
摘要
针对无人机在战场上通信环境恶劣、信道统计信息未知及抗智能性干扰能力差等问题,研究了多域抗干扰问题,提出一种多域联合抗干扰智能决策算法。在频域上采取信道选择的方式应对干扰,将其建模成一个多臂老虎机信道选择问题,并对信道干扰等级进行评判;对于中度干扰的信道进行功率域上的压制性对抗,将其建模成Stackelberg博弈模型,并求解博弈均衡,得出最佳发射功率,减少频繁切换信道带来的系统开销。仿真结果表明所提算法的系统长期回报明显高于传统多臂老虎机算法和随机选择算法,并且还提高了通信系统的平均吞吐量。
Key words: multi-domain anti-jamming / multi-arm slot machine / channel selection / Stackelberg game
关键字 : 多域抗干扰 / 多臂老虎机 / 信道选择 / Stackelberg博弈
© 2021 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
在未来战场无人机作战将是主要作战形式之一,无人机通信系统的可靠性和有效性是制约其作战效能的重要因素。因此研究无人机通信系统可靠的通信抗干扰方式至关重要。
智能干扰和认知干扰的出现,给无人机通信抗干扰工作带来了巨大的挑战。为了有效对抗智能干扰,提高无人机通信系统的通信质量也就成了热点研究内容[1]。目前,因为智能算法的兴起,利用智能决策算法去对抗智能干扰的研究越来越多,他们大致可以分成两大类:一类是在频域上进行认知抗干扰,主要是通过频繁的切换信道来躲避干扰的攻击。例如文献[2]利用深度Q网络学习算法在频域上进行信道选择。文献[3]研究了认知网络中的抗干扰问题,提出了一种信道快速选择算法。文献[4]提出了一种利用博弈论抗干扰的方案,并给出了相应的信道选择算法。另一类是在功率域上进行智能抗干扰,根据干扰的发射功率调整自己的发射功率来应对攻击。典型的如文献[5-6]利用博弈论的分析方法在功率域上进行抗干扰。文献[7]将功率域抗干扰问题建模成一个非零和博弈模型,获得了用户的最佳发射功率。文献[8]把用户作为领导者,干扰机作为跟随者,将功率域抗干扰问题建模成stackelberg博弈模型,得到了对抗双方的最佳发射功率。为了更好地应对干扰攻击,学者们又提出了多域联合的抗干扰方法。例如文献[9-10]设计出了一种速率自适应和信道选择相结合的抗干扰算法,其性能优于单独采用这2种方法中的任意一种。文献[11]考虑了位置移动特性和信道的切换,提出了一种二维联合抗干扰算法。文献[12]利用遗传算法对多个抗干扰参数实现了重新配置。但是,以上大多数多域联合抗干扰算法是将多维决策排列在一个更大的一维决策空间中,其本质还是在一维上解决问题。
根据以上分析,本文将功率域和频域上的抗干扰算法结合起来,提出一种基于多臂老虎机(multi-armed bandit, MAB)和stackelberg博弈的多域抗干扰智能决策算法。在信道统计信息未知的情况下,先是通过频谱感知,利用多臂老虎机进行信道选择,并对各信道干扰情况进行层次划分,即分成轻度干扰、中度干扰和重度干扰3个层次。当上一时隙所选信道在当前时隙被判定为中度干扰时,不进行信道切换,而是在功率域建立Stackelberg博弈模型进行抗干扰。通过解出纳什均衡获得通信方最佳发射功率和最佳效用。所提算法不仅提高了通信系统抗干扰的可靠性和有效性,还减少了信道切换开销,实现了智能抗干扰。
1 系统模型
系统模型如图 1所示,无人机通信系统包括发送方和接收方, 还有一个恶意干扰机。现将无线网络频谱分成n个互相独立的信道, 定义信道集N={1, 2, 3, ⋯, N}, 信道带宽为Bn。当信道可用时定义状态为“1”, 不可用时定义其状态为“0”。故信道可用状态矢量为Q=(Q1, Q2, ⋯Qn)。其中, Qn∈(0, 1)。本文设定干扰机具有一定智能性, 可以利用频谱感知技术去感知用户信道, 也可以根据用户的策略和环境信息调整自己的干扰策略, 如切换干扰信道和调整干扰功率等, 以求自身效益最大化。信道统计状态信息是未知的, 假设在每个时隙发送方只选择一个信道进行传输, 恶意干扰机也只能选择一个信道进行干扰[13]。用户在时隙t选择可用信道ω(t)进行传输信息, 获得的回报可以定义为:
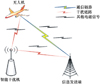 |
图 1 无人机多域抗干扰系统模型 |
2 多域抗干扰智能决策算法研究
2.1 基于MAB模型的频域抗干扰算法
在通信方对信道状态统计信息未知的情况下, 如何选择可靠有效的信道已被建模成一个MAB问题[14]。多臂老虎机是一种具有强大学习能力的新型动态随机控制模型, 他主要应用于路由选择、信道分配和伺机频谱接入等问题。
基于改进的UCB索引策略[15], 本节提出一种考虑信道切换开销的信道选择抗干扰算法。改进后的索引值由两部分组成:第一部分为目前被选信道的预期平均回报; 第二部分为改进的置信因子。根据文献[14], 划分的每个信道都可以看成一个臂。在时隙t, 设通信方选择某个臂ω(t)便可获得一个回报r(t)。χn(t)表示信道n在经过t个时隙后被选择的次数, 可表示为
(2)式中δ{·}是指示函数, 其定义为
定义S(t)表示在t个时隙中信道切换次数
为了减少信道的探索成本, 引入收益值方差来调节探索过程, 可反映出在未来时刻收益波动情况。
式中:rn(k)表示在第k个时隙中信道n的瞬时收益;rn(t)表示信道n在经过t个时隙后平均收益。
根据(5)式可得到一个偏差因子, 其数学表达式为
通过进一步调整改进, 得到最终的改进的索引值
通信方会遍历所有信道, 根据得到的索引值来决定下一个时隙的选择。这里, 通信方将选取具有最大的μn*的信道。
在时隙t
定义选择信道n的期望回报为
式中,E[·]是求期望操作。
在t个时隙中, 定义累积回报为
期望的累积回报为:
假设单位信道切换所需代价为b, 则期望的信道开销可以定义为
把信道开销看成一种性能损失, 则通信方所获得的长期回报定义为
研究信道选择问题就是为了使系统收益回报最大。在MAB问题中, 评判此类算法的好坏常用悔恨值这一性能指标[16],它表示通信方没有选择最佳臂而造成的损失。故通信系统的最大收益也可以用系统的最小悔恨值来等价代替, 把信道切换开销考虑进去, 在经历t个时隙后的悔恨值为
式中, un*=max un, n=1, 2, ⋯, M, E[A*(t)]是E[A(t)]的上界, 即E[A*(t)]≥E[A(t)]。
本文主要研究的目标函数为(16)式, 现为了验证所选性能指标的合理性与可行性, 进行如下推理分析和证明。
推论1 系统得到的悔恨值函数随着时间呈对数变化, 即E[R(t)]~O(lgt)。且悔恨值函数收敛存在上界。
证明1 根据参考文献[17]所述的定理1, 可以推得
式中,Δn=u*-un。再根据文献[18]提供的定理可得
同样根据参考文献[18]所述定理可得
证毕。
通过改进的USB索引算法决策出各个信道干扰情况后, 选择最佳信道进行信息传输并且根据既定的信道干扰容限阈值PJth1与PJth2将信道所受干扰功率划分成3个等级, 即轻度、中度、重度干扰。
信道的干扰等级划分
2.2 Stackelberg功率控制博弈抗干扰算法
根据2.1节得出的结论, 当上一时隙所选信道在当前时隙被判定为中度干扰, 则立即对此信道进行Stackelberg功率控制博弈抗干扰, 不进行信道切换。并且通过求解博弈均衡得到通信方最佳传输功率, 实现功率域抗干扰。
参考文献[13]中的论述, 假定信道增益在一个时隙内不会发生变化只会在下一个时隙随机变化, 定义通信方的接收端和发送端之间的信道增益为
式中:ds为通信方发射端和接收端的距离;βs是路径衰落因子;εs是瞬时衰落系数。
同理, 定义干扰机和接收端之间的链路增益为
式中:dj为通信方接收端和干扰机的距离;βj是路径衰落因子;εj是瞬时衰落系数。
假设通信方为领导者, 干扰机是跟随者。定义博弈模型数学表达式为
根据文献[19-20],假定通信方在时隙t选择了信道n,基于接收信号的信干噪比, 通信方在时隙t的效用函数定义为
式中:Qn是所选信道可用状态;P表示通信方发射功率;J表示干扰机发射功率;Bn表示所选信道带宽;N0是噪声功率谱密度;Ys是通信方单位发射功率代价。
同理, 可以定义干扰机的效用函数为
式中, Yj是干扰机单位发射功率代价。
本文采用经典的Stackelberg博弈分析方法——逆向归纳法。通信方的优化问题可以表示为求取最佳发射功率即Stackelberg均衡
式中, Pmax是通信方最大发射功率。同理, 干扰机的优化问题可以表示为
式中, Jmax是干扰机的最大干扰功率。通过计算得到Stackelberg均衡, 表示无论通信方还是干扰机都无法通过单方面改变策略而提高自己的效用。
定理2 通信方的最佳发射功率PsSE和最佳效用us*分别为
证明2 根据文献[19-20]的论述分析, 这里采用逆向归纳法进行证明。
假定通信方的功率策略是P, 当Qn=1时, 有
所以, 干扰机的效用函数是干扰功率的凹函数。通过引入非负对偶变量ξ, 干扰机的优化问题的拉格朗日函数可定义成下式
根据库恩-塔克条件[21], 可以得到
根据(30)式, 可以得到干扰机的最佳干扰功率
式中, 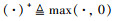 。当Qn=0时, 干扰机的效用函数uj=(P, J)=-YjJ是干扰功率J的单调递减函数。
。当Qn=0时, 干扰机的效用函数uj=(P, J)=-YjJ是干扰功率J的单调递减函数。
同理, 根据通信方的优化问题, 把(31)式代入(23)式中可得
式中
当满足P≤ϕ时, 通信方的效用函数us是发射功率P的线性函数。当满足P>ϕ时, 可以得到
所以, 通信放的效用函数是发射功率P的凹函数。同理, 通过引入非负对偶变量ϑ, 通信方的优化问题的拉格朗日函数可以定义为
与干扰机的分析过程类似, 通信方的最佳发射功率为
当满足条件Ys≤εs(ds)-βs/(2BnN0)-ϑ时, 通信方的博弈均衡最佳发射功率PsSE=Ps*。这时, 通信方的最佳效用是
当满足条件εs(ds)-βs/(2BnN0)- ϑ ≤Ys≤εs(ds)-βs/BnN0时, 通信方的博弈均衡最佳发射功率PsSE=ϕ。这时, 通信方的最佳效用是
当满足条件εs(ds)-βs/BnN0≤Ys时, 通信方的博弈均衡最佳发射功率为PsSE=0。这时, 通信方的最佳效用是us*=0。当满足条件Qn=0时通信方的效用函数us(P, J)=-YsP是发射功率P的减函数。所以通信方的最佳发射功率PsSE和最佳效用us*均为0。
证毕。
2.3 多域抗干扰智能决策算法描述
通过以上分析, 把频域和功率域2种域上的抗干扰算法相结合, 得出的多域抗干扰智能决策算法流程如图 2所示。
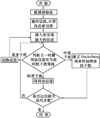 |
图 2 多域抗干扰智能决策算法流程 |
算法 多域抗干扰智能决策算法(MAIDA)
step 1 数据初始化, 确定最大迭代次数Nt, 干扰容限阈值PJth1、PJth2, 令t=0, Sn(0)=0, χn(0)=0, r(0)=0;
step 2 遍历所有信道, 每个信道都要在时隙结束前根据历史信息算出改进后的索引值;
step 3 在时隙t, 选择计算出的改进索引值最大的信道进行信息传输;
step 4 更新t=t+1, 如果上一时隙所选信道在当前时隙被判定为轻度干扰, 则继续在该信道进行信息传输; 若判定为中度干扰, 则在功率域直接建立一个Stackelberg博弈功率抗干扰模型, 由博弈均衡得出最佳传输功率; 若判定为重度干扰, 则发射功率为零, 转至step3;
step 5 根据公式依次更新: Sn(t), χn(t), r(t);
step 6 当迭代次数达到最大值Nt时, 算法终止。
3 实验仿真及结果分析
3.1 实验条件及参数设置
为验证本文所提算法的有效性, 对系统获得的累积悔恨值、长期回报、瞬时回报和平均吞吐量等性能指标进行仿真。仿真硬件平台是Inter(R) Core(TM), 2.6 GHz, 内存为8 GB的PC机, 所有实验均在MATLAB R2016a环境下进行。
参考文献[13-14]参数设置如下: 设共有10个信道, 噪声功率谱密度N0=-130 dB/Hz, 信道带宽Bn=2.5 MHz, 衰落因子βs=βj=3, 通信距离ds=10 km, dj=40 km, Pmax=30 W, Jmax=60 W。
仿真结果是进行200次蒙特卡洛仿真取平均值的结果。
3.2 仿真结果分析
为了验证所提MAIDA算法面对智能性干扰对信道干扰情况判决的准确性,对信道在不同时隙下的改进索引值进行仿真。由仿真数据可绘制如图 3所示的信道索引图。
 |
图 3 MAIDA算法对信道干扰情况的等级划分 |
从图 3可得出MADIA可以对信道干扰情况进行判决,并划分干扰等级,为下一步在什么时隙哪个信道进行功率域抗干扰提供参考。
从仿真图 4可知,单位信道切换开销b对系统的累积悔恨值有一定影响。累积悔恨值随着单位信道开销b的增大而增大。因为单位信道开销越大,对系统的通信性能损失越大。从图中还可以看出,MADIA得到的累积悔恨值与时隙呈对数变化关系,这也验证了证明1。
 |
图 4 累积悔恨值与单位切换开销的关系 |
为验证所提MAIDA的性能,与2种不同算法的长期回报进行对比。从仿真图 5中可以看出,通信系统采用MAIDA可以获得更大的长期回报。因为传统MAB算法会在每个时隙都进行信道选择,这将会增大信道切换开销。至于随机选择算法其获得的长期回报最小,因为其每个时隙都随机切换信道,对抗干扰不具有针对性。
 |
图 5 不同算法获得的累积回报性能对比 |
为进一步验证MAIDA的性能,仿真分析了3种算法的期望回报速率,即瞬时回报。瞬时回报越高说明算法性能越好。从仿真6图可以看出,MAIDA的瞬时回报要明显高于其他2种算法,说明MAIDA性能要更优越。
 |
图 6 不同算法获得的瞬时回报性能对比 |
仿真图 7给出了上述3种算法的系统平均吞吐量随时间变化曲线。由图 7可知,3种算法的平均吞吐量曲线走势均是先快速增加,然后增速变慢,最后趋于平缓。所提MAIDA的系统平均吞吐量明显高于另外2种算法,并且随着时间的推移无限趋近于通信上界。
 |
图 7 不同算法获得的系统平均吞吐量随时间变化关系曲线 |
以上仿真实验是MAIDA算法与频域或功率域上的抗干扰算法性能对比,验证了本文所提算法抗干扰效果明显好于单一域抗干扰。现对采用MAIDA算法和当前其他2种多域抗干扰算法的通信系统的误码率进行仿真,比较他们的抗干扰性能。认知无线电和多输入多输出技术相结合的算法(cognitive radio-mutiple input multiple output, CR-MIMO),实现了频域、时域、空域上的混合式抗干扰;空时直扩通信系统与多输入多输出技术相结合的抗干扰算法(space-time direct spread MIMO, STDS-MIMO), 实现了信息在时域、空域、功率域上的多域传输,大大提高了抗干扰能力。
 |
图 8 不同多域抗干扰算法的通信系统误码率随信干比变化曲线 |
由仿真结果可以看出,3种算法在低信干比下,都可以保持较低的误码率,说明抗干扰效果都很好。但是,在相同信干比下,MAIDA算法的通信系统误码率还是明显低于其他2种算法的,这也说明了本文算法抗干扰能力更强。
4 结论
为解决无人机在战场上面对复杂电磁环境及智能性干扰通信较困难的问题,提出了多域联合抗干扰智能决策算法。此算法基于多臂老虎机在信道统计信息未知的情况下研究了信道选择问题,并根据计算得出的改进的索引值对信道干扰等级进行划分。根据干扰等级,选择信道基于Stackelberg博弈模型在功率域上进行抗干扰,减少信道切换开销,提高通信系统的长期回报值,得到了更高的系统平均吞吐量。通过仿真与其他多域抗干扰算法进行对比,说明该算法抗干扰性能更优越。
References
- Gupta L, Jain R, Vaszkun G, et al. Survey of important issues in UAV communication networks[J]. IEEE Communications Surveys and Tutorials, 2016, 18(2):1123–1152 [Article] [Google Scholar]
- Wang S, Liu H, Gomes P H, et al. Deep reinforcement learning for dynamic multichannel access in wireless networks[J]. IEEE Trans on Cognitive Communications and Networking, 2018, 4(2):257–265 [Article] [Google Scholar]
- Wu Y, Wang B, Liu K. Anti-jamming games in multi-channel cognitive radio networks[J]. IEEE Journal of Selected Areas in Communications, 2012, 30(1):4–15 [Article] [Google Scholar]
- Chen C, Song M, Xin C, et al. A game-theoretical anti-jamming scheme for cognitive radio networks[J]. IEEE Network, 2013, 27(3):22–27 [Article] [Google Scholar]
- Xiao L, Chen T, Liu J, et al. Anti-jamming transmission Stackelberg game with observation errors[J]. IEEE Communications Letters, 2015, 19(6):949–952 [Article] [Google Scholar]
- Ahmedi K, Fapojuwo A O. Stackelberg equilibria of an anti-jamming game in cooperative cognitive radio networks[J]. IEEE Trans on Cognitive Communications and Networking, 2018, 4(1):121–134 [Article] [Google Scholar]
- Altman E, Avrachenkov K, Garnaev A. A jamming game in wireless networks with transmission cost[C]//International Conferene on Network Control and Optimization, 2007 [Google Scholar]
- Yang D, Zhang J, Fang X, et al. Optimal transmission power control in the presence of a smart jammer[C]//IEEE Global Communications Conference, 2012 [Google Scholar]
- Hanawal M K, Abdelrahman M J, Krunz M, et al. Joint adaptation of frequency hopping and transmission rate for anti-jamming wireless systems[J]. IEEE Trans on Mobile Computing, 2016, 15(9):2247–2259 [Article] [Google Scholar]
- Hanawal M K, Abdelrahman M J, Krunz M, et al. Game theoretic anti-jamming dynamic frequency hopping and rate adaptation in wireless systems[C]// Modeling and Optimization in Mobile, Adhoc and Wireless Networks, 2014 [Google Scholar]
- Han G, Xiao L, Poor H V. Two-dimensional anti-jamming communication based on deep reinforcement learning[C]//IEEE International Conference on Acoustics, Speech and Signal Processing, 2017 [Google Scholar]
- Jin H, Song X, Wang M, et al. A fast anti-jamming decision method based on the rule-reduced genetic algorithm[J]. KSII Trans on Internet and Information Systems, 2016, 10(9):4549–4567 [Article] [Google Scholar]
- Wu Q, Xu Y, Wang J, et al. Distributed channel selection in time-varying radio environment: interference mitigation game with uncoupled stochastic learning[J]. IEEE Trans on vehicular technology, 2013, 62(9):4524–4538 [Article] [Google Scholar]
- Chen L, Iellamo S, Coupechoux M, et al. Opportunistic spectrum access with channel switching cost for cognitive radio networks[C]//International Conference on Communications, 2011: 1–5 [Google Scholar]
- Zhu Jiang, Chen Hongcui, Xiong Jiahao. Channel selection baseed on multi-armeed slot machine moedel[J]. Telecommunications Technology, 2015, 55(10):1094–1100 [Article] [Google Scholar]
- Du Z, Wu Q, Yang P, et al. Learning with handoff cost constraint for network selection in heterogeneous wireless networks[C]//Communications and Mobile Computing, 2016, 16(4): 441–458 [Google Scholar]
- Auer P, Cesabianchi N, Fischer P, et al. Finite-time analysis of the multiarmed bandit problem[J]. Machine Learning, 2002, 47(2):235–256 [Article] [Google Scholar]
- Qin Z, Wang J, Chen J, et al. Opportunistic channel access with repetition time diversity and switching cost: a block multi-armed bandit approach[J]. Wireless Networks, 2018, 24(5):1683–1697 [Article] [Google Scholar]
- Yang D, Xue G, Zhang J, et al. Coping with a smart jammerin wireless networks: a Stackelberg game approach[J]. IEEE Trans on Wireless Communications, 2013, 12(8):4038–4047 [Article] [Google Scholar]
- Xiao L, Chen T, Liu J, et al. Anti-jamming transmission stackelberg game with observation errors[J]. IEEE Communications Letters, 2015, 19(6):949–952 [Article] [Google Scholar]
- Boyd S, Vandenberghe L. Convex optimization, Cambridge: Cambridge University Press, 2004 [Google Scholar]
All Tables
All Figures
 |
图 1 无人机多域抗干扰系统模型 |
| In the text | |
 |
图 2 多域抗干扰智能决策算法流程 |
| In the text | |
 |
图 3 MAIDA算法对信道干扰情况的等级划分 |
| In the text | |
 |
图 4 累积悔恨值与单位切换开销的关系 |
| In the text | |
 |
图 5 不同算法获得的累积回报性能对比 |
| In the text | |
 |
图 6 不同算法获得的瞬时回报性能对比 |
| In the text | |
 |
图 7 不同算法获得的系统平均吞吐量随时间变化关系曲线 |
| In the text | |
 |
图 8 不同多域抗干扰算法的通信系统误码率随信干比变化曲线 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


