| Issue |
JNWPU
Volume 39, Number 3, June 2021
|
|
|---|---|---|
| Page(s) | 463 - 470 | |
| DOI | https://doi.org/10.1051/jnwpu/20213930463 | |
| Published online | 09 August 2021 | |
Numerical investigation on fluid dynamic characteristics around shoulder ventilation of submarine-launched vehicle
潜射航行体肩部通气流体动力特性数值研究
1
School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China
2
Key Laboratory of Unmanned Underwater Vehicle Technology, Northwestern Polytechnical University, Xi’an 710072, China
施瑶(1988-), 西北工业大学副研究员, 主要从事跨介质航体水动力特性研究。e-mail: shiyao@nwpu.edu.cn
Received:
25
September
2020
In order to study the influence of the ventilating cavitation flow at the shoulder of a submerged-launched vehicle on the surface hydrodynamic characteristics, a three-dimensional potential model for the shoulder ventilation of the vehicle was established based on the homogeneous multiphase flow theory, standard RNG k-ε model, Singhal cavitation model and overlapping grid technology, and the numerical simulation of the unsteady evolution process of the ventilated cavitation flow was carried out, and the cavitation flow morphology evolution, surface pressure distribution and resistance characteristics under different ventilation rates were compared. The results showed that the thickness and length of the ventilated cavitation flow in the early stage of fusion continue increased with the increasing of ventilation volume, and its thickness and length changed slightly in the later stage; when the exhaust position did not change and the ventilation volume was within a certain range, the differential pressure resistance coefficient and viscous resistance coefficient decreased with the increasing of internal pressure of the ventilated cavity.
摘要
为研究潜射航行体肩部通气空泡流对其表面流体动力特性的影响,基于均质多相流理论、标准RNG k-ε模型、Singhal空化模型以及重叠网格技术,建立三维潜射航行体肩部通气模型,开展通气非定常空泡流演变过程数值模拟研究,对比了不同通气量下空泡流形态演化、表面压力分布以及阻力特性。结果表明:当通气量增加到一定值后,通气空泡流在融合前期其厚度与长度不断增大,后期其厚度和长度基本保持不变;当排气位置不变、通气量在一定范围的条件下,通气空泡内压增大,压差阻力系数和黏性阻力系数呈减小趋势。
Key words: submarine-launched vehicle / ventilation mass flow / cavitation flow / hydrodynamics
关键字 : 潜射航行体 / 通气量 / 空泡流 / 流体动力
© 2021 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
潜射航行体水下垂直发射过程一般包含3个阶段, 即出筒阶段、自由航行阶段以及出水阶段[1]。在出水阶段, 航行体头部穿越自由液面, 空泡发生溃灭, 对航行体结构产生较大的冲击载荷[2]。研究表明, 通过人工通气的方法提高航行体空泡内压力可有效减小冲击载荷[3]。因此研究航行体肩部通气出水过程具有非常重要的意义。
国内外相关学者对通气空泡流开展了大量的工作, 并取得了一定的成果。Reichardt等[4]首次提出利用人工通气的方法生成类似“超空泡”来改善航行体表面流体动力特性; 基于此通气方法, 后续许多学者开展了相关研究。Silberman等[5]研究了水翼在通气空泡流的振荡规律, 获得了通气量与空泡流形态以及泡内压力之间的关系。王海斌等[6]在水洞开展了水下航行体通气超空泡的试验研究, 研究了通气率和弗劳德数对空泡形态和模型阻力系数的影响; 王复峰等[7]采用试验和仿真相结合方法对绕带空化器回转体通气过程进行了研究; 张孝石等[8]在水洞研究了不同空化数下航行体表面压力脉动特性。孙铁志等[9]基于均质平衡流理论和动网格技术、SST湍流模型和各相间的质量输运方程, 开展了通气位置对潜射航行体流体动力特性影响研究; 李国良等[10]研究了通气时序、通气方式等对空泡形态以及出水载荷的影响; 张素宾等[11]采用数值模拟方法, 对航行体水下垂直发射过程的通气空泡流开展了研究, 分析了通气空泡的演化规律及流动特征。于娴娴等[12]利用数值模拟方法研究了通气质量流量和动量流量对航行体表面流体动力特性的影响。虽然目前关于通气空泡流的研究已取得了一定的研究成果, 但主要集中于水洞条件下的通气超空泡领域, 针对潜射航行体肩部通气改善其流体动力特性相关研究文献较少。
因此获取航行体肩部通气空泡流形态演变、表面压力系数分布以及阻力特性等变化规律, 对后续潜射航行体肩部通气出水试验设计及流体动力特性预测提供技术支撑。
1 数值计算方法
1.1 控制方程
描述航行体水下垂直发射气液多相流动的基本控制方程包括连续性方程、动量方程、能量方程, 其基本形式如下。
连续性方程
动量方程
能量方程
1.2 湍流方程
本文采用标准的RNG k-ε模型, 通过修正湍流黏度, 考虑了平均流动中的旋转和旋流流动情况, 能更好地处理高应变率以及流线弯曲程度较大的流动。
1.3 空化模型
本文采用Singhal空化模型, 其计算公式如下
1.4 重叠网格技术
重叠网格的节点有3种, 分别为洞内点、计算点以及插值点。洞内点不参与流场计算、计算点参与流体计算, 插值点进行流场信息的传递, 其中3种网格节点在重叠网格分布如图 1所示, 具体的实现流程如图 2所示。
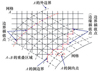 |
图1 重叠网格示意图 |
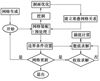 |
图2 重叠网格实现流程图 |
1.5 数值算法验证
为了验证本文数值模拟方法的有效性, 利用相关文献[13]试验数据进行验证。根据上述试验建立三维圆柱壳体匀速出水过程数值计算方法, 利用STAR CCM流体计算软件展开精细化数值计算, 其中边界条件如图 3所示, 此外, 为了保证计算精度, 同时尽可能降低计算量, 因此本文采用半圆柱壳体模型展开数值方法验证, 其中网格划分示意图如图 4所示。
图 5为气泡生长过程实验和仿真对比图, 从图中可以发现气泡随时间逐渐生长过程中可以发现, 气泡形态演变过程基本相似, 其上部呈现梯状下端呈球状。但是由于数值计算过程中半圆柱体壳体表面设置为无滑移光滑壁面, 并且无接触角, 所以与实验形态具有一定的差异。因此, 针对数值模拟计算得到的相图而言, 生成的气泡大体上较为接近, 在本文数值验证可接受范围内。
从图 6和图 7可知, 试验中空泡长度和厚度与数值计算之间的最大误差分别为5.25%, 9.85%, 误差在可接受范围内, 所以可以认为本研究方法在计算空泡长度和厚度发展过程是有效的。
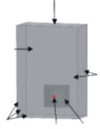 |
图3 边界条件设置 |
 |
图4 网格划分 |
 |
图5 气泡生长过程实验与仿真对比 |
 |
图6 空泡长度演变图 |
 |
图7 空泡厚度演变图 |
2 数值计算模型
2.1 几何模型与网格划分
首先建立三维潜射航行体肩部通气模型, 如图 8所示, 其中模型直径为D, 长径比L/D=6, 头型采用椭球型。通气孔口位置距离航行体头部L1, 孔口直径d≈0.02D, 孔间距比s/d≈2.2。本文所涉及参考量为水的密度、航行体直径D、长度L、初始速度V以及重力g, 从而将时间t*、压力p*、空泡长度L*、厚度D*参量进行无量纲处理,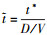 ,
,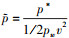 ,
,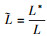 ,
,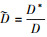 ,即考虑到本文研究是航行体肩部通气一自由度水下垂直发射过程, 为控制计算成本和提高计算效率, 截取1/2潜射航行体流场计算域开展数值模拟。
,即考虑到本文研究是航行体肩部通气一自由度水下垂直发射过程, 为控制计算成本和提高计算效率, 截取1/2潜射航行体流场计算域开展数值模拟。
图 9选用航行体头部顶点初始位置作为笛卡尔坐标系的原点, 重力方向沿着Z轴负方向, 参考压力为101 325 Pa, 自由液面Z轴坐标为+3L, 则整个水域沿着Z轴的压力呈ρg(3L-z)。此外航行体头部距离水面3L, 距离底部1.5L, 自由液面之上的空气域高度为1.5L, 计算域为半圆柱体, 直径为16D。
边界条件设置如图 9所示, 计算域分为背景域和子域, 其中背景域上端和侧面为压力出口, 底端为无滑移壁面, 截面为对称平面; 子域中航行体设置为不可滑移壁面, 孔口为质量流量入口。最后, 本文为了研究不同通气量对潜射航行体空泡流形态及流体动力特性影响, 保持孔径大小不变, 只须将通气量作为唯一变量即可。
图 10为模型网格划分以及表面Y+分布, 采用STAR CCM软件进行网格划分, 对背景域中航行体运动区域和水面附近进行网格加密。
其中背景网格全部为切割体网格, 子域网格采用多面体网格, 边界层采用棱柱层网格, 层数为25。此外, 分别对重叠区域航行体肩部和孔口附近进行二次加密, 来捕捉孔口附近空泡流演化细节。航行体壁面Y+分布在0~40之间, 完全满足对空泡流形态演变进行精细化捕捉。
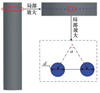 |
图8 潜射航行体几何模型 |
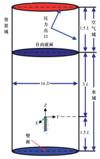 |
图9 计算域边界条件设置 |
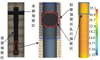 |
图10 模型网格细节划分以及表面Y+分布 |
2.2 网格无关性验证
针对上述潜射航行体模型, 开展了粗糙尺度网格(270万)、中等尺度网格(610万)与精细尺度网格(850万)计算结果对比, 不同尺度网格计算下航行体表面压力分布如图 11所示。从图中可以看出粗糙尺度网格计算结果与中等、精细尺度网格差异较大, 而中等尺度网格域精细尺度网格计算结果基本一致。考虑到计算成本和效率, 故选取中等尺度网格(610万)开展数值计算, 满足重叠网格计算要求。
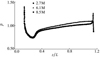 |
图11 不同网格尺度下航行体表面压力对比 |
3 数值结果与分析
3.1 通气空泡形态分析
图 12为典型工况下潜射航行体肩部通气空泡流演化过程, 其中航行体发射速度为8 m/s, 孔口排气流量为0.1 kg/s, 空化数为0.3。由图可知, 潜射航行体肩部通气过程空泡流演化过程可分为3个阶段: 空泡融合、空泡发展、空泡脱落等典型过程。空泡流融合阶段是指航行体肩部不同孔口空泡流由初始束状融合成面状, 直至包裹航行体肩部通气孔下部区域, 如图 12所示, 即0~0.1 s。在此阶段中, 当航行体肩部开始通气时, 孔口空泡流由单个束状空泡组成, 呈上方细长下方球状形态。随着航行体不断向水面运动过程中, 肩部通气空泡在空间位置不断扩张, 其形态逐渐由周向束状演变成条带状, 并发生周向融合, 直至基本包裹航行体肩部通气孔下部区域, 如图 13所示。通气空泡在轴向和周向方向不断扩张的动力来源主要是孔口附近高压气体不断的注入。此外, 还有横向水流的剪切以及周围环境压降等共同作用, 直至空泡流完全包裹航行体孔口以下表面, 如图 14所示; 空泡流发展过程是指通气空泡流完全包裹孔口以下表面后, 随着航行体向自由液面运动过程中, 周围水的静压梯度不断减小, 通气空泡流不断发展, 此过程中伴随着少量空泡流脱落, 即0.2~0.36 s; 空泡流脱落过程是指当航行体头部触及自由液面时, 包裹航行体表面的空泡流开始脱落, 直至航行体完全出水, 即0.40~0.44 s。
本文为研究通气量对潜射航行体空泡流形态演变影响, 在保证孔径大小、位置等参数不变的条件下, 开展了不同通气量数值模拟计算工况, 即0.05, 0.1, 0.15 kg/s。图 15为不同通气量下空泡流融合前期厚度演变散点图, 由图可知, 随着通气量增大, 气泡流厚度也呈递增趋势。主要是因为通气空泡开始时, 径向速度较大, 泡内压力较大, 此时驱动气泡流不断膨胀发展的不是其航行体所受阻力, 而是泡内外压差, 从而导致空泡迅速径向膨胀, 厚度不断增加, 但随着径向速度衰减, 空泡口都增长趋势有所减小。图 16为空泡流融合后期厚度演变散点图, 由图可知, 空泡流融合后期厚度基本保持不变。图 17为不同通气量下空泡流融合前期长度演变散点图, 由图可知随着通气量增大, 空泡流融合前期长度呈线性增长, 但增长趋势有所衰减。孔口附近空泡流轴向速度较大, 故而其呈线性增长。图 18为不同通气量下空泡流融合后期长度演变散点图, 在水的静压梯度、阻力等共同作用下, 其轴向速度呈减小趋势, 直至包裹整个航行体表面。
 |
图12 航行体肩部通气空泡流形态演化过程 |
 |
图13 空泡流融合前期形态由束状向面状演化过程 |
 |
图14 空泡流融合后期形态由面状发展至包在航行体表面过程 |
 |
图15 空泡流融合前期厚度演变图 |
 |
图16 空泡流融合后期厚度演变图 |
 |
图17 空泡流融合前期长度演变散点图 |
 |
图18 空泡流融合后期长度演变散点图 |
3.2 潜射航行体表面压力特性分析
图 19给出了不同通气率下的航行体表面压力系数与无通气条件下表面压力系数的对比。从图中可以发现, 通气量为0.05 kg/s工况下, 表面压力系数与无通气孔表面压力系数差别较小。主要原因通气量太小, 导致空泡流还未发生融合就已经发生了脱落; 此外, 从图中还发现, 通气孔口压力骤然上升, 主要原因如下: 图 20为典型工况下通气空泡融合前孔口压力云图, 空泡融合前期径向速度较大, 孔口处压力较小; 随着通气空泡流由束状开始发生融合, 空泡径向速度大于空泡流融合速度, 导致孔口处通气空泡流径向速度减小, 压力骤然上升。此外, 在航行体孔口下方存在近似等压区, 主要原因在于通气空泡由孔口排出时, 其形态逐渐由束状掺混融合形成面状, 完全包裹航行体质心偏上区域; 而航行体质心以下区域其表面压力存在波动现象, 主要是由于此范围的通气空泡发生了部分脱落, 并未完全包裹航行体。当航行体出水过程中通气空泡发生了脱落及溃灭现象, 但航行体表面压力并未发生较大的变化。可见, 不同通气量会导致航行体表面压力产生较大差异, 所以合理设计通气量大小有助于改变航行体表面压力分布, 从而改善其表面流体动力特性。
 |
图19 不同通气量下航行体表面压力系数 |
 |
图20 通气空泡融合过程中孔口压力云图 |
3.3 潜射航行体阻力特性分析
表 1为不同通气量下潜射航行体阻力系数演变过程, 其中, Cp为压差阻力系数、CW为黏性阻力系数、CR为总阻力系数。从表 1中可以看出, 在通气位置一定的条件下, 不同通气量对航行体阻力系数影响较大。当通气量为0.05 kg/s时, 阻力系数未发生明显变化, 主要原因如上所述, 空泡未发生融合, 而且此工况下航行体基本处于全沾湿状态, 导致阻力系数基本未发生变化。
当通气量为0.10 kg/s时, 空泡发生融合并包裹航行体表面, 总阻力减小11.18%, 其中压差阻力减小6.12%, 黏性阻力减小55.7%;当通气量为0.15 kg/s时, 总阻力减小11.78%, 主要原因在于通气量不断增大, 通气空泡在航行体运动过程脱落量增加, 从而航行体阻力基本趋于定值。由此可见, 在通气位置相同条件下, 通气量直接影响航行体阻力特性, 因此合理的通气量能够有效减小航行体所受阻力。
不同通气量下阻力系数演变过程
4 结论
本文基于均质多相流理论、标准RNG k-ε模型、Singhal空化模型以及重叠网格技术, 建立了三维潜射航行体肩部通气数值计算模型, 模拟了不同通气量下潜射航行体肩部通气空泡流形态以及表面流体动力特性演变过程, 获得了以下结论:
1) 潜射航行体空泡流前期在泡内压力作用下沿着径向不断膨胀, 导致空泡厚度不断增加, 但后期增长趋势减小; 空泡流在水的压力梯度、黏性阻力以及惯性等共同作用下沿着轴向不断发展, 直至包裹航行体孔口以下表面。随着通气量增加, 空泡流融合前期厚度和长度都呈增大趋势, 后期基本保持不变。
2) 表面压力分布: 在保持通气位置不变的条件下, 随着通气率增大, 泡内压力增大, 导致潜射航行体孔口下方表面压力系数有所增加, 从而改善航行体表面压力分布。
3) 阻力特性演变: 在一定通气量范围内, 增大通气量, 航行体所受黏性阻力和压差阻力逐渐减小, 可有效减小航行体所受阻力。
References
- Wang Yiwei, Huang Chenguang. Research progress on hydrodynamics of high speed vehicles in the underwater launching process[J]. Advances in Mechanics, 2018, 48: 259–298 [Article] (in Chinese) [Google Scholar]
- Wang Yiwei, Hang Chenguang, Du Tezhuan, et al. Mechanism analysis about cavitation collapse load of underwater vehicles in a vertical launching process[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(1): 39–48 [Article] (in Chinese) [Google Scholar]
- Savchenko Y N. Control of supercavitation flow and stability of supercavitating motion of bodies[R]. Brussels, RTO-AVT and VKI, 2001 [Google Scholar]
- Reichardt H. The laws of cavitation bubbles as axially symmetrical bodies in a flow[M]. Britain: Kaiser Wilhelm Institute, 1945 [Google Scholar]
- Silberman E, Song C S. Instability of ventilated cavities[J]. Journal of Ship Research, 1961, 5(1): 13–33 [Google Scholar]
- Wang Haibin, Zhang Jiazhong, Wei Yingjie, et al. Experimental study of the drag reduction of ventilated supercavity of underwater bodies[J]. Ship Engineering, 2006(3): 14–17 10.3969/j.issn.1000-6982.2006.03.014 (in Chinese) [Google Scholar]
- Wang Fufeng, Wang Guoyu, Huang Biao, et al. Experimental and numerical study on characteristic of ventilated cavitation multiphase flow[J]. Engineering Mechanics, 2016, 33(9): 220–226 [Article] (in Chinese) [Google Scholar]
- Zhang Xiaoshi, Wang Cong, Zhang Naimin, et al. Tests for pressure fluctuating characteristics around a ventilated underwater vehicle[J]. Journal of Vibration and Shock, 2017, 36(17): 85–90 [Article] (in Chinese) [Google Scholar]
- Sun Tiezhi, Wei Yingjie, Wang Cong, et al. Analysis of the effect of ventilation positions on hydrodynamic characteristics of submarine-launched vehicle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(10): 1303–1308 [Article] (in Chinese) [Google Scholar]
- Li Guoliang, Shang Qing, Tian Junwu, et al. Effect of ventilation cavitation launching on water-exit for submarine vehicle[J]. Physics of Gases, 2016, 1(3): 39–46 [Article] (in Chinese) [Google Scholar]
- Zhang Subin, Lou Chuanjing, Chen Xin. Investigation of ventilated cavity shapes of a high speed underwater vehicle[J]. Journal of Shanghai Jiaotong University, 2012, 46(2): 329–334 [Article] (in Chinese) [Google Scholar]
- Yu Xianxian, Wang Yiwei, Huang Chenguang, et al. Parameters and influence of gas injection on modification of cavitation stability[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2015, 45(3): 53–63 [Article] (in Chinese) [Google Scholar]
- Wei Qiaodong. Research on experimental characteristics of underwater porous exhaust[D]. Harbin: Harbin Engineering University, 2016(in Chinese) [Google Scholar]
All Tables
All Figures
 |
图1 重叠网格示意图 |
| In the text | |
 |
图2 重叠网格实现流程图 |
| In the text | |
 |
图3 边界条件设置 |
| In the text | |
 |
图4 网格划分 |
| In the text | |
 |
图5 气泡生长过程实验与仿真对比 |
| In the text | |
 |
图6 空泡长度演变图 |
| In the text | |
 |
图7 空泡厚度演变图 |
| In the text | |
 |
图8 潜射航行体几何模型 |
| In the text | |
 |
图9 计算域边界条件设置 |
| In the text | |
 |
图10 模型网格细节划分以及表面Y+分布 |
| In the text | |
 |
图11 不同网格尺度下航行体表面压力对比 |
| In the text | |
 |
图12 航行体肩部通气空泡流形态演化过程 |
| In the text | |
 |
图13 空泡流融合前期形态由束状向面状演化过程 |
| In the text | |
 |
图14 空泡流融合后期形态由面状发展至包在航行体表面过程 |
| In the text | |
 |
图15 空泡流融合前期厚度演变图 |
| In the text | |
 |
图16 空泡流融合后期厚度演变图 |
| In the text | |
 |
图17 空泡流融合前期长度演变散点图 |
| In the text | |
 |
图18 空泡流融合后期长度演变散点图 |
| In the text | |
 |
图19 不同通气量下航行体表面压力系数 |
| In the text | |
 |
图20 通气空泡融合过程中孔口压力云图 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


