EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 43 / No 3 (June 2025) JNWPU, 43 3 (2025) 467-477 Full HTML
Open Access
Issue
JNWPU
Volume 43, Number 3, June 2025
Page(s) 467 - 477
DOI https://doi.org/10.1051/jnwpu/20254330467
Published online 11 August 2025

© 2025 Journal of Northwestern Polytechnical University. All rights reserved.

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

可靠性分析的目的是求解工程系统在各种不确定性因素影响下, 实现规定功能的概率, 即可靠度。近几十年来, 静态可靠性分析领域已发展了多种方法[1-3], 其中最具代表性的是基于最大可能点(most probable point, MPP)的方法[4]。但这些方法无法解决包含时变不确定性问题。近年来, 时变可靠性分析受到越来越多关注, 成为可靠性分析领域的前沿课题。目前文献中已有的时变可靠性分析方法大致分为2类: 基于极值的方法和基于首次穿越的方法。

基于极值的时变可靠性分析方法[5-7]一般求解过程是: 先确定系统时变响应的极值分布, 然后根据极值分布求解时变可靠度。Chen等[5]提出构造一个与时变响应随机过程的极值相关的虚拟随机过程, 进而计算时变可靠度。Li等[6]提出一种双层循环优化方法, 在内层优化循环确定动态响应达到极值的时间, 在外层优化循环通过搜索最大可能点计算可靠度。由于直接求解系统响应极值的概率密度函数非常困难, 许多研究人员提出使用代理模型预测时变响应的极值分布。Wang等[7]提出一种嵌套极值响应面方法, 在随机输入空间构建响应面, 预测时变响应达到极值的时间, 然后将时变可靠性约束转换为静态可靠性约束, 但该方法采用的双层循环结构计算量很大。Hu等[8]提出一种基于抽样和鞍点近似的方法, 但无法处理显含时间的时变功能函数。考虑到构建极值响应面的难度, 一些研究人员提出对系统原始时变功能函数建立代理模型, 间接获取时变响应的极值分布。Wang等[9]发展了一种等价随机过程转换方法(equivalent stochastic process transformation, eSPT), 将时变极限状态函数转换为一个时间无关函数, 并采用Kriging对其进行近似。

基于首次穿越的时变可靠性分析方法[10-12]依赖于穿越事件的概念, 具体是指系统时变响应越过约束的最大边界, 由正常状态转为失效状态的事件。穿越率则指某一瞬时穿越事件发生的概率。将穿越率函数在指定时间区间内积分, 即可得到时变可靠度。Bell实验室的Rice[10]于20世纪40年代提出了著名的穿越率计算公式。基于所有穿越事件相互独立的假设下, Andrieu-Renaud等[11]提出了著名的PHI2方法, 通过求解一个两单元并行系统可靠性问题得到穿越率。Sudret[12]进一步提出PHI2+方法, 提高了计算稳定性。Hu等[13]为考虑穿越事件的相关性, 提出一种基于联合穿越率的方法, 相较PHI2+提高了精度, 但也增加了计算量。

最近几年, 为了避免计算复杂的穿越率函数, 发展了一类基于时间离散的时变可靠性分析方法[14-15]。2014年, 湖南大学的Jiang等[16]提出一种TRPD方法, 将一个时变极限状态函数离散为多个时间独立极限状态函数, 之后Jiang等[17]又对该方法做了改进。Gong等[18]将时间区间离散为大量等间距时间节点, 然后在每个时间节点上搜索MPP, 并使用一阶可靠度方法(first order reliability method, FORM)计算瞬时可靠度, 最后用多维正态分布函数求解时变可靠度。2021年, 笔者提出了一种最大可能轨迹法(approximating most probable point trajectory, AMPPT)[19], 将静态可靠性分析中最大可能点的概念推广至时变可靠性领域, 建立了“最大可能轨迹”概念, 并提出采用主动学习方法建立其Kriging模型, 进而计算时变可靠度, 显著简化了时变可靠性分析过程。但是, 以上方法均为一阶时变可靠性分析方法, 当时变可靠性问题的非线性程度较高时, 可能导致较大误差。在静态可靠性分析领域, 研究人员发展了二阶可靠度方法(second order reliability method, SORM)[20]来提高非线性可靠性分析问题的精度。Hu等[21]结合极值方法和二阶鞍点近似, 发展了一类二阶时变可靠性分析方法, 但该方法仅能用于处理具有显式时间输入的功能函数。除此之外, 尚未见其他二阶时变可靠性分析方法的公开发表。

1 一阶时变可靠性分析方法及不足

1.1 时变可靠性分析问题的定义

时变可靠性分析的目的是求解工程系统在时变不确定性因素影响下, 在规定时间[ts, te]内, 始终保持可靠的概率。时变可靠性分析问题的一般数学模型表示为

式中: P{·}为概率算子; g(X, Y (t), t)为一般时变功能函数，g(X, Y (t), t) < 0表示系统安全; X =[X1, X2, …, Xn]T表示n维随机向量; Y (t)=[Y1(t), Y2(t), …, Ym(t)]T为m维随机过程向量; t为时间参数。根据(1)式, 时变失效概率可相应地表示为

1.2 一阶时变可靠性分析的AMPPT方法

[ts, te]内任意时刻ti对应的瞬时极限状态方程为g(X, Y (ti), ti)=0。通过求解(3)式中的等式约束优化问题, 可得到对应的最大可能点。

式中: u是由[X, Y (ti)]映射变换(如Nataf变换[22])所得的标准正态随机向量; Gti(u)表示标准正态空间(U空间)中与g(X, Y (ti), ti)等价的瞬时功能函数。

在AMPPT方法中, 笔者将“最大可能轨迹”定义为: 在ti从ts变化到te的过程中, 将每个时刻的最大可能点连接起来, 在U空间中形成的一条有向曲线 u MPP(t)。最大可能轨迹为时变功能函数g(X, Y (t), t)的固有属性, 在数学上, 它是一个以时间为参数的一元向量函数; 在几何上, 它是(n+m)维U空间中的一条轨迹。

AMPPT方法利用主动学习技术建立最大可能轨迹的近似模型 û MPP(t), 并基于串联系统可靠性计算理论[17], 推导了其与时变可靠度之间的数学关系。限于篇幅, 此处不再详述。

AMPPT方法在每一时刻均将瞬时功能函数在 u MPP(ti)处一阶泰勒展开, 从而将瞬时响应等价为正态变量, 相应地, 时变响应被等价为高斯过程。但当g(X, Y (t), t)的非线性程度较高时, 一阶展开可能导致较大的计算误差。

2 Hessian矩阵迭代逼近方法

为提高对具有较高非线性时变可靠性分析问题的求解精度, 本文提出在 u MPP(ti)处建立Gti(u)的二阶近似模型。二阶近似模型的构建需要求解函数Gti(u)在 u MPP(ti)处的Hessian矩阵 H =▽2Gti(uMPP(ti)), 但有限差分法的计算量过大。对此, 本节引入基于迭代逼近的Hessian矩阵求解方法, 在求解uMPP(ti)的同时, 得到近似的H。

2.1 iHL-RF算法

Zhang等[23]提出了一种iHL-RF算法, 被广泛应用于MPP搜索，具体如下:

给定起始搜索点后, iHL-RF算法通过迭代搜索MPP点。迭代公式为

式中：d (j)为搜索方向; λ(j)为步长。

d (j)的计算方法为

式中, ▽Gti(u (j))为Gti(u)在 u (j)处的一阶梯度向量, 可用有限差分法计算。

λ(j)可通过求解(6)式中的Armijo一维线搜索问题获得

式中：k为非负整数; a和b为(0, 1)内的常数。

重复上述迭代过程, 直至满足以下条件

式中, ε为一个收敛误差阈值。当(7)式中的终止条件成立时, 搜索点序列收敛于Gti(u)的MPP点, Gti(u)在搜索点的一阶梯度向量也收敛于其在 u MPP(ti)处的一阶梯度向量。

2.2 Hessian矩阵高效近似方法

对称秩一(symmetric rank-one, SR1)校正方法可以通过对一个简单初始矩阵迭代校正, 逐渐逼近真实Hessian矩阵[24]。本文在iHL-RF算法的迭代过程中, 使用SR1校正估计Gti(u)的Hessian矩阵。具体的Hessian矩阵迭代公式为

式中: s (j)为连续2次迭代中的搜索点坐标之差; y (j)为连续2次迭代中的搜索点的一阶梯度向量之差, 即

在序列点{ u (j)}收敛于MPP点 u MPP(ti)的过程中, 矩阵序列 HSR1(j)也收敛于瞬时功能函数Gti(u)的真实Hessian矩阵 H。

3 基于Hessian矩阵逼近的二阶时变可靠性分析方法

3.1 瞬时功能函数的二阶抛物面近似

获得ti∈[ts, te]时刻的MPP点及对应的Hessian矩阵 H后, 可将瞬时功能函数Gti(u)在 u MPP(ti)处二阶泰勒展开为

式中, J =▽Gti(u MPP(ti))为瞬时功能函数Gti(u)在 u MPP(ti)处的Jacobian矩阵。

在可靠性分析时, 只需关注瞬时功能函数的符号, 其具体数值大小不影响可靠度。因此可对(10)式等号右边除以正数‖ J ‖来进行化简, 而

对U空间进行旋转变换, 构造V随机空间, 使V空间与U空间的原点重合, 而其第(n+m)个坐标轴指向U空间中MPP点 u MPP(ti), 如图 1所示。

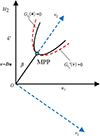thumbnail 图1

V随机空间中的二阶抛物面模型示意图

V空间是由U空间旋转变换而来, 因此两者间的映射关系可用一个正交矩阵 D表示，其可通过Gram-Schmidt正交化方法[25]得到。

获得正交矩阵 D后，根据其性质 D T= D -1，可得U空间中任意一点 u与其在V空间中对应点 v的映射关系为

同理可得V空间中MPP点坐标vMPP(ti)为

将 u = D T v代入(11)式得

式中, A = DBD T。

令 A ′为 A的前(n+m-1)行、前(n+m-1)列元素组成的子矩阵, 则 A ′的特征值κj(j=1, 2, …, n+m-1)即为极限状态边界Gti(D T v)=0在 v MPP(ti)点的前(n+m-1)阶主曲率。根据Zhao等[26]的研究，可得到极限状态边界Gti(D T v)=0在 v MPP(ti)点的各维度平均曲率半径R和V空间中的二阶抛物面模型G′ti(v)，具体见(15)~(16)

式中, vj(j=1, 2, …, n+m)是向量 v的第j分量。

由(16)式可知，G′ti(v)可视为两部分的加权和，即

式中: 由于-β为常数，vn+m为标准正态变量，故θ(v)为正态变量；δ(v)为(n+m-1)个标准正态变量的平方和，即为自由度为(n+m-1)的中心χ2分布随机变量；1/(2R)为δ(v)的权重系数。由(17)式可见：

1) 若Gti(u)的非线性程度较低，其极限状态边界接近于一个超平面，MPP点处平均曲率半径R较大。此时，1/(2R)趋于0，二阶抛物面近似模型退化为线性近似模型；

2) 若Gti(u)的非线性程度较高，则极限状态边界在MPP点处平均曲率半径R较小。此时，δ(v)具有较大的权重系数1/(2R)，其可作为一阶近似项θ(v)的修正项，提高近似精度。

由此可见，在平均曲率半径计算较为准确时，二阶抛物面近似模型由于充分考虑了MPP点处的曲率，能实现比AMPPT方法中的一阶近似模型更高的精度。

3.2 基于原始随机空间采样的二阶时变可靠度计算方法

基于3.1节建立的二阶抛物面模型，将瞬时响应转化为一个正态随机变量和一个χ2分布随机变量之加权和的形式后，对应的时变响应为一个非高斯非平稳随机过程(non-Gaussian nonstationary process, NNP)[27]。但目前的随机过程模拟方法，都只适用于平稳或非平稳的高斯过程[28]。而如何准确地模拟一般的NNP，仍是一个具有挑战性的工作。

为此，本节提出一种在原始随机空间采样的方法计算二阶时变可靠度。在原始随机空间对各输入随机变量和随机过程进行采样模拟，然后通过Nataf变换和正交变换，将这些样本转换至V空间，之后代入V空间中每一时刻的二阶抛物面模型中，计算二阶时变可靠度。

3.2.1 构建平均曲率半径函数的Kriging模型

由(17)式可知，瞬时功能函数的二阶抛物面近似模型共包含2个参数：u MPP(ti)和平均曲率半径R。当ti在[ts, te]内改变时，u MPP(ti)和R都随ti而改变，如图 2所示。

thumbnail 图2

各时刻对应的MPP点处平均曲率半径示意图

因此，平均曲率半径R与 u MPP(t)一样，也是时间t的函数，记为R(t)。为了得到任意时刻ti∈[ts, te]对应的 u MPP(ti)和R(ti)，本节通过构建Kriging模型u MPP(t) 和，分别对 u MPP(t)和R(t)进行近似。

首先，采用自适应采样方法，建立最大可能轨迹的Kriging模型 û MPP(t)。在ti时刻采样时，不仅搜索MPP点 u MPP(ti)，还同时执行本文第2节介绍的Hessian矩阵迭代逼近过程，得到 u MPP(ti)处的Hessian矩阵 H (ti)。在自适应采样过程结束后，可得到1组“时间-Hessian矩阵”样本{(ti, H (ti)) i =1, 2, …, Nc}。根据(15)式，计算对应的平均曲率半径R(ti)，从而获得“时间-平均曲率半径”样本{(ti, R(ti)) i =1, 2, …, Nc}。

以{(ti, R(ti)) |i =1, 2, …, Nc}为初始样本，建立一个单输入单输出Kriging模型。设对应的预测标准差函数为σR(t)。

求解(18)式中的优化问题，得到 的预测标准差最大的时刻t*。

检查最大预测标准差σR(t*)是否满足终止条件

式中，etarget为预测标准差阈值。若不满足，则在t*时刻执行MPP搜索，得到Hessian矩阵 H (t*)，计算平均曲率半径R(t*)。最后，将新样本(t*, R(t*))加入训练样本集合，并更新Kriging模型 。重复以上过程，直到终止条件(19)式成立，即可得到足够精确的。

3.2.2 在原始随机空间采样并变换至V空间

得到ûMPP 和 后, 在原始随机空间对输入随机向量 X和随机过程向量Y (t)进行采样, 并将样本变换至V空间。

根据随机向量 X =[X1, X2, …, Xn]T的分布, 生成其单个样本 x =[x1, x2, …, xn]T。将时间区间[ts, te]离散为s个等间距时刻点ti(i=1, 2, …, s), 然后根据 Y (t)=[Y1(t), Y2(t), …, Ym(t)]T的各个随机过程分量Yj(t) (j=1, 2, …, m)的特征函数, 采用扩展最优线性估计(expansion optimal linear estimation, EOLE)方法[28]，生成 Y (t)的单个样本 y m×s，如(20)式所示。

式中, y j=[y1(t1), y1(t2), …, y1(ts)]表示Yj(t)(j=1, 2, …, m)的样本, yj(ti)表示随机过程Yj(t)在ti(i=1, 2, …, s)时刻的取值。

在ti(i=1, 2, …, s)时刻, 利用Nataf变换将这一组随机变量转换至U空间

将ti代入u MPP(t), 可得到ti时刻MPP点ûMPP(ti)。根据 û MPP(ti)和Gram-Schmidt正交化方法，建立正交矩阵 D。利用(22)式中的正交变换，将U空间中的随机向量ûi转换至V空间，即

同理，将全部时刻ti(i=1, 2, …, s)的输入随机向量[x1, x2, …, xn, y1(ti), y2(ti), …, ym(ti)]T进行Nataf变换和正交变换后，即可得到1组V空间中的随机向量{ v 1, v 2, …, v s}。

3.2.3 基于MCS方法计算二阶时变可靠度

将随机向量组{ v 1, v 2, …, vs}代入二阶抛物面模型(17)式，求解瞬时响应G′ ti(v i)(i=1, 2, …, s)，并定义指示函数I({ v 1, v 2, …, vs})为

由(23)式可知，当I(H)=0时系统失效。

最后，生成随机向量 X的NMCS个样本 x (k)(k=1, 2, …, NMCS)和随机过程向量 Y (t)的NMCS个样本 y m×s(k)(k=1, 2, …, NMCS)，重复以上过程，则可得二阶时变可靠度为

综上所述，本文提出的SOTRM方法计算步骤如图 3所示。

thumbnail 图3

SOTRM求解流程图

3.3 与一阶时变可靠性分析方法的对比

表 1从MPP搜索、瞬时和时变响应的建模方式、需构建的Kriging模型、MCS采样方式等5个方面，对本文提出的SOTRM方法与AMPPT方法进行了对比。

表1

一阶与二阶时变可靠性分析方法的对比

本文提出的SOTRM方法充分考虑了每一时刻极限状态边界在其MPP点处的曲率信息，对于非线性程度较强的问题，能有效提高瞬时可靠度指标和时变可靠度的计算精度。

4 算例

采用3个典型算例，对本文提出的SOTRM方法的精度和效率进行验证，对比算法包括AMPPT和MCS方法，其中MCS方法的结果作为时变可靠度的参考基准。当估计值的变异系数小于5%时，认为MCS方法收敛。

4.1 非线性函数算例

非线性函数算例[29]的表达式为

式中式中, 随机变量X1~N(3.7, 0.62), X2~N(4, 0.62), 时间参数t∈[0, 5]。

分别采用MCS、AMPPT和本文SOTRM方法求解该问题。图 4给出在t=5时刻，瞬时极限状态边界的一阶线性近似模型和本文的二阶抛物面近似模型的对比曲线。图 5给出本文SOTRM方法的最终时变可靠性分析结果与AMPPT和MCS方法的精度对比。

thumbnail 图4

t=5时刻瞬时极限状态边界的一、二阶近似模型对比

thumbnail 图5

非线性函数算例的时变可靠性分析结果曲线

从图 4可以明显看到，该函数算例在t=5时刻，对应的瞬时极限状态边界在其MPP点处具有较强的非线性，采用一阶线性近似模型将产生较大的近似误差，而本文的二阶抛物面模型可以显著提高近似精度。

图 5a)瞬时可靠度指标随时间变化的曲线表明，SOTRM方法得到的二阶瞬时可靠度指标与MCS结果几乎完全相同，而AMPPT得到的一阶瞬时可靠度指标在t∈[0, 5]范围内，始终小于MCS的基准值。AMPPT方法得到的一阶瞬时可靠度指标偏小，是因为瞬时极限状态边界相对于U空间的坐标原点内凹，且AMPPT方法的一阶瞬时可靠度指标的偏小量，等于概率密度函数在图 4中的阴影部分的积分。图 5b)给出了失效概率变化曲线。可以看到，SOTRM方法得到的累积失效概率与MCS的基准值几乎完全一致，而AMPPT方法由于低估了瞬时可靠度，其累积失效概率在t∈[0, 5]范围内，始终高于MCS的基准值。

表 2汇总了3种方法在本算例中的时变可靠性分析结果。表中MCS结果后的括号为其变异系数的值。AMPPT方法结果与MCS的相对误差高达18.42%，而SOTRM方法的相对误差仅为0.02%，验证了本文方法的精度优势。

表2

非线性函数算例的时变可靠性分析结果

4.2 某折叠翼飞行器算例

本算例对某折叠翼飞行器的机翼展开过程[30]时变可靠性进行分析。机翼的展开过程受到伺服主动力矩MA和外部气动阻力矩MR的影响。MR与机翼展开角θ的关系如表 3所示。MR与θ及攻角α的关系如表 4所示。

表3

不同机翼展开角时的主动力矩MA

表4

不同攻角和机翼展开角时的气动阻力矩MR  N·m

受加工制造、装配及飞行器实际飞行状态等方面的随机影响，主动力矩MA、阻力矩MR、机翼转动惯量I和机翼展开时的攻角α都存在不确定性。由于机翼展开过程较快，假设飞行器攻角在展开过程中保持不变。该飞行器的设计技术指标要求机翼能在1 s内从0°展开至90°。该问题涉及的随机变量及其分布如表 5所示。

表5

折叠翼飞行器的不确定性参数分布

机翼展开过程可由(26)式表示。

式中, ω(t)表示机翼的展开角速度。初始条件为: θt=0=0, ωt=0=0。

折叠翼的展开角度θ(t)为一个随机过程, 该折叠翼飞行器问题的时变功能函数为

式中, θ*=90°表示最大展开角度。本问题中的累积失效概率定义为

图 6给出了3种方法的瞬时可靠度指标曲线。AMPPT所得的一阶瞬时可靠度指标β(t)始终高于MCS基准值，而SOTRM方法与MCS方法更加接近。

thumbnail 图6

折叠翼算例的瞬时可靠度指标曲线

图 7给出3种方法所得的累积失效概率随时间变化曲线。表 6给出时变可靠性分析的详细结果。

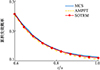thumbnail 图7

折叠翼算例的累积失效概率曲线

表6

折叠翼算例的时变可靠性分析结果

可见，AMPPT方法始终低估了机翼展开的失效概率，而本文的SOTRM方法与MCS方法的基准值更加接近。

4.3 高维悬臂梁算例

本节例考虑一个高维的悬臂梁结构时变可靠性分析问题[22]。如图 8所示，悬臂梁左端固支, 右端自由，受到2个动态集中力F1(t)和F2(t)、2个弯矩M1和M2以及2个分布载荷q1和q2的作用。ai, bi, ci和di(i=1, 2)分别表示弯矩、集中力和分布载荷到悬臂梁固支端的距离，qLi和qRi分别为分布载荷的左端和右端值。

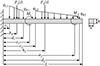thumbnail 图8

悬臂梁结构示意图

记悬臂梁的长度为L，其矩形截面的宽和高分别为w和h。在本例中，将悬臂梁所受到的载荷、载荷作用位置和悬臂梁的几何参数作为不确定性参数，共19个。其中，动态集中载荷F1(t)和F2(t)分别被建模为平稳和非平稳高斯过程。

在该问题中，定义失效为悬臂梁自由端挠度大于许可值Δallow=0.013 m时，故时变功能函数为

可通过(30)~(32)式计算得到。

式中: E=200×109 Pa为材料的弹性模量；I=wh3/12为截面惯性矩；M和R为固支端的弯矩和反作用力。不确定性参数的分布如表 7所示。

表7

高维悬臂梁的不确定性参数分布

表中，μ (t)为F2(t)的均值函数，表达式如(33)式所示。

本例中还引入了同样采用Kriging模型的eSPT方法为对比算法，设置eSPT方法的初始采样数为40，自适应采样停止准则为累积置信度大于等于0.999或建模样本数大于2 000。

图 9给出了各方法计算的累积失效概率曲线。从图 9可以看出，本文所提出的SOTRM方法的结果与MCS方法最为接近。表 8给出了高维悬臂梁算例时变可靠性分析的具体结果。

thumbnail 图9

高维悬臂梁算例的累积失效概率曲线

表8

高维悬臂梁算例的时变可靠性分析结果

从表 8中可以看出，在精度方面，AMPPT和SOTRM方法相对于MCS方法的误差分别为2.43%和0.03%，SOTRM精度更高。相比之下，eSPT方法的相对误差达到了60.77%，远高于AMPPT和SOTRM方法。从计算效率看，eSPT调用2 000次功能函数。而AMPPT和SOTRM的调用次数均为240次，远小于eSPT方法。

本例的结果表明，相比于AMPPT方法，本文所提出的SOTRM方法能在不增加计算成本情况下，有效提高对非线性问题的求解精度；相比于对时变功能函数进行直接建模的单层Kriging方法，SOTRM方法仅需构造单输入Kriging模型。在面对高维时变可靠性分析问题时，SOTRM构建Kriging的难度和成本都更低。

5 结论

目前时变可靠性分析方法的研究大多基于FORM方法，二阶时变可靠性分析方法的研究较少。本文重点针对功能函数非线性程度较高情况下的问题，提出一种通用的高精度二阶时变可靠性分析方法：

1) 充分考虑瞬时功能函数的曲率信息，建立其二阶抛物面近似模型，从而将瞬时响应建模为正态随机变量和χ2分布随机变量加权和的形式，将时变响应描述为一般的NNP，提高了近似精度；

2) 采用基于对称秩一校正法，在迭代搜索最大可能点的同时，逐步逼近瞬时功能函数的Hessian矩阵，避免了直接计算Hessian矩阵带来的巨大计算量；

3) 提出基于原始随机空间采样的方法，避免了对时变响应NNP进行精确数值模拟的困难。

3个算例的结果表明，本文提出的SOTRM方法能有效提高时变可靠性分析的精度。SOTRM方法对于提高时变可靠性分析方法在实际工程中的适用范围具有重要意义。

References

  1. LI X, GONG C L, GU L X, et al. A sequential surrogate method for reliability analysis based on radial basis function[J]. Structural Safety, 2018, 73: 42–53 [Article] [Google Scholar]
  2. DU X P, CHEN W. A most probable point-based method for efficient uncertainty analysis[J]. Journal of Design and Manufacturing Automation, 2001, 4(1): 47–66 [Google Scholar]
  3. PAFFATH M, WEVER U. Adapted polynomial chaos expansion for failure detection[J]. Journal of Computational Physics, 2007, 226(1): 263–281 [Article] [Google Scholar]
  4. YOUN B D, CHOI K K, DU L. Adaptive probability analysis using an enhanced hybrid mean value method[J]. Structural and Multidisciplinary Optimization, 2005, 29(2): 134–148 [Article] [Google Scholar]
  5. CHEN J B, LI J. The extreme value distribution and dynamic reliability analysis of nonlinear structures with uncertain parameters[J]. Structural Safety, 2007, 29(2): 77–93 [Google Scholar]
  6. LI J, CHEN J B, FAN W L. The equivalent extreme-value event and evaluation of the structural system reliability[J]. Structural Safety, 2007, 29(2): 112–131 [Article] [Google Scholar]
  7. WANG Z Q, WANG P F. A nested extreme response surface approach for RBDO with time-dependent probabilistic constraints[C]//38th Design Automation Conference, Chicago, 2012: 735–744 [Google Scholar]
  8. HU Z, DU X P. A sampling approach to extreme value distribution for time-dependent reliability analysis[J]. Journal of Mechanical Design, 2013, 135(7): 1–8 [Google Scholar]
  9. WANG Z Q, CHEN W. Time-variant reliability assessment through equivalent stochastic process transformation[J]. Reliability Engineering & System Safety, 2016, 152: 166–175 [Google Scholar]
  10. RICE S O. Mathematical analysis of random noise[J]. Bell Labs Technical Journal, 1944, 24(1): 46–156 [Article] [Google Scholar]
  11. ANDRIEU-RENAUD C, SUDRET B, LEMAIRE M. The PHI2 method: a way to compute time-variant reliability[J]. Reliability Engineering & System Safety, 2004, 84(1): 75–86 [Article] [Google Scholar]
  12. SUDRET B. Analytical derivation of the outcrossing rate in time-variant reliability problems[J]. Structure and Infrastructure Engineering, 2008, 4(5): 353–362 [Google Scholar]
  13. HU Z, DU X P. Time-dependent reliability analysis with joint upcrossing rates[J]. Structural and Multidisciplinary Optimiza-tion, 2013, 48(5): 893–907 [Article] [Google Scholar]
  14. HU Z, MAHADEVAN S. Time-dependent system reliability analysis using random field discretization[J]. Journal of Mechanical Design, 2015, 137(10): 101404[Article] [Google Scholar]
  15. HU Z, DU X P. First order reliability method for time-variant problems using series expansions[J]. Structural and Multidisciplinary Optimization, 2015, 51(1): 1–21 [Google Scholar]
  16. JIANG C, HUANG X P, HAN X, et al. A time-variant reliability analysis method based on stochastic process discretization[J]. Journal of Mechanical Design, 2014, 136(9): 91009[Article] [Google Scholar]
  17. JIANG C, WEI X P, WU B, et al. An improved TRPD method for time-variant reliability analysis[J]. Structural and Multidisciplinary Optimization, 2018, 58(5): 1935–1946 [Article] [Google Scholar]
  18. GONG C Q, FRANGOPOL D M. An efficient time-dependent reliability method[J]. Structural Safety, 2019, 81: 101864 [Google Scholar]
  19. ZHANG Y W, GONG C L, LI C N. Efficient time-variant reliability analysis through approximating the most probable point trajectory[J]. Structural and Multidisciplinary Optimization, 2021, 63(1): 289–309 [Article] [Google Scholar]
  20. HU Z, MANSOUR R, OLSSON M, et al. Second-order reliability methods: a review and comparative study[J]. Structural and Multidisciplinary Optimization, 2021, 64(6): 3233–3263 [Google Scholar]
  21. HU Z, DU X P. Second order reliability method for time-dependent reliability analysis using sequential efficient global optimization[C]//45th Design Automation Conference, Anaheim, California, USA, 2019 [Google Scholar]
  22. LIU P L, KIUREGHIAN A D. Multivariate distribution models with prescribed marginals and covariances[J]. Probabilistic Engineering Mechanics, 1986, 1(2): 105–112 [Article] [Google Scholar]
  23. ZHANG Y, KIUREGHIAN A D. Reliability and optimization of structural systems[M]. Boston: Springer US, 1995: 297–304 [Google Scholar]
  24. LIM J M, LEE B C, LEE I. Second-order reliability method-based inverse reliability analysis using Hessian update for accurate and efficient reliability-based design optimization[J]. International Journal for Numerical Methods in Engineering, 2014, 100(10): 773–792 [Google Scholar]
  25. ADHIKARI S. Reliability analysis using parabolic failure surface approximation[J]. Journal of Engineering Mechanics, 2004, 130(12): 1407–1427 [Article] [Google Scholar]
  26. ZHAO Y G, ONO T. New approximations for SORM: part 1[J]. Journal of Engineering Mechanics, 1999, 125: 86–93 [Article] [Google Scholar]
  27. XU F Y, MA X L. An efficient simulation algorithm for non-Gaussian nonstationary processes[J]. Probabilistic Engineering Mechanics, 2021, 63: 103105 [Google Scholar]
  28. GHANEM R G, SPANOS P D. Stochastic finite elements: a spectral approach[M]. New York: Springer-Verlag, 1992 [Google Scholar]
  29. HAWCHAR L, EI-SOUEIDY C P, SCHOEFS F. Global kriging surrogate modeling for general time-variant reliability-based design optimization problems[J]. Structural and Multidisciplinary Optimization, 2018, 58(3): 955–968 [Google Scholar]
  30. LIU Yingwei, ZHENG Dongqing, HOU Junping, et al. Reliability analysis for the deploying mechanism of missile wing[J]. Hongdu Science and Technology, 2001(1): 53–57 (in Chinese) [Google Scholar]

All Tables

表1

一阶与二阶时变可靠性分析方法的对比

In the text
表2

非线性函数算例的时变可靠性分析结果

In the text
表3

不同机翼展开角时的主动力矩MA

In the text
表4

不同攻角和机翼展开角时的气动阻力矩MR  N·m

In the text
表5

折叠翼飞行器的不确定性参数分布

In the text
表6

折叠翼算例的时变可靠性分析结果

In the text
表7

高维悬臂梁的不确定性参数分布

In the text
表8

高维悬臂梁算例的时变可靠性分析结果

In the text

All Figures

thumbnail 图1

V随机空间中的二阶抛物面模型示意图
In the text
thumbnail 图2

各时刻对应的MPP点处平均曲率半径示意图
In the text
thumbnail 图3

SOTRM求解流程图
In the text
thumbnail 图4

t=5时刻瞬时极限状态边界的一、二阶近似模型对比
In the text
thumbnail 图5

非线性函数算例的时变可靠性分析结果曲线
In the text
thumbnail 图6

折叠翼算例的瞬时可靠度指标曲线
In the text
thumbnail 图7

折叠翼算例的累积失效概率曲线
In the text
thumbnail 图8

悬臂梁结构示意图
In the text
thumbnail 图9

高维悬臂梁算例的累积失效概率曲线
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.