| Issue |
JNWPU
Volume 39, Number 2, April 2021
|
|
|---|---|---|
| Page(s) | 249 - 257 | |
| DOI | https://doi.org/10.1051/jnwpu/20213920249 | |
| Published online | 09 June 2021 | |
Cooperative control method of multi-missile formation under uncontrollable speed
速度不可控条件下的多弹编队协同控制方法
1
School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China
2
Spacecraft Survival Technology and Effectiveness Evaluation Laboratory, Beijing 100085, China
Received:
4
August
2020
Under the missile speed is uncontrollable, a design method of multi-missile formation flight controller based on the sliding mode variable structure control theory and adaptive dynamic surface control theory is proposed. Firstly, according to the relative position of the leader and the follower in the inertial frame, the tracking error model for the relative position and the expected relative position between the leader and the follower is obtained, and the multi-missile formation control system in the inertial coordinate system is obtained. Secondly, in order to obtain the expression of the formation control system in the ballistic coordinate system, the acceleration of the missile in the ballistic coordinate system is converted to the inertial coordinate system. Combining with the tracking of the relative position and the desired relative position of the leader and the followers, we can obtain the simplified error model for the formation control system. Then the sliding mode variable structure control theory and the adaptive dynamic surface control theory are used to design the formation controllers for the leader and follower missiles respectively, and the stability of the present controller is analysed via the Lyapunov stability theory. Finally, the designed formation controllers are used for the leader and follower missiles to simulate the parameters. The results verify the feasibility and effectiveness of the present method.
摘要
在导弹速度不可控的前提下,提出了一种基于滑模变结构控制理论和自适应动态面控制理论的多弹编队飞行控制器设计方法。在惯性系下对编队模型进行描述,即根据领弹和从弹在惯性系下的相对位置,求得领弹和从弹间的相对位置与期望相对位置的跟踪误差模型;为了得到编队控制系统在弹道坐标系下的表达式,将导弹在弹道坐标系下的俯仰和偏航通道加速度转换到惯性坐标系下,结合领弹和从弹的相对位置与期望相对位置的跟踪误差模型,经过化简得到无需进行速度控制的编队控制系统的具体模型,并且采用滑模变结构控制理论和自适应动态面控制理论分别对领弹和从弹进行编队控制器设计,利用Lyapunov稳定性理论分析了所提控制器的稳定性;领弹和从弹均采用设计好的编队控制器进行参数仿真,结果验证了新方法的可行性和有效性。
Key words: multi-missile formation / sliding mode variable structure control / dynamic surface / a leader-follower strategy
关键字 : 多弹编队 / 滑模变结构控制 / 动态面 / 领弹-从弹策略
© 2021 Journal of Northwestern Polytechnical University. All rights reserved.
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
近年来,随着各国导弹防御系统的发展,单枚导弹的突防、攻击等能力受到威胁,不能胜任现阶段对其提出的要求。多枚导弹组成的编队系统,在作战过程中通过信息交互,共同完成目标搜索、突防、饱和攻击等作战任务,极大地提高了导弹的突防能力和打击能力,增加了摧毁目标的概率,因此研究多弹编队飞行具有非常重要的现实意义。
目前编队控制器的设计多集中在无人机,究其原因,无人机可以对速度进行实时控制,容易设计编队控制器以及应用到现实中。Tahk等提出了仅使用视线角度信息来实现飞行器编队的控制器设计方法。因为测量视线角度不需要飞行器之间的数据通信,所以该方法是有用的,并且后续对多飞行器编队飞行进行了仿真,验证了所提控制器的可行性和有效性[1]。Dogan等提出了一种生成安全可行轨迹的重新配置无人机编队的算法,给出了当前位置和要去的位置。位置跟踪控制器的设计采用积分控制、最优LQR设计和非线性状态反馈线性化相结合的重新配置无人机编队的非线性控制器的方法[2]。Giulietti等讨论了编队飞行的2个方面:动态建模和编队控制。在编队飞行中,考虑飞行动力学是由气动效应耦合得到,提出了一种“分布式马蹄涡理论”,建立了准确的动力学方程,并在此基础上,设计了一种允许轨迹跟踪和编队几何保持的编队控制器。仿真结果表明,所设计的控制器在双机编队中表现出较好的性能[3]。为了减少多智能体编队队形变换带来的能量消耗,Ajorlou等提出了一种两阶段能量最优重构策略,它是指在当前任务发布到下一个队形变换命令之间的空闲时间,将智能体移动到一个特殊编队。仿真结果表明,该策略相比传统策略可以大大降低能耗[4]。文献[5]与文献[4]的方法相同,只是用编队队形变换时间的控制替换了对能量的控制。Zhao等针对四旋翼无人机编队控制问题,采用一种分层方法,由上层的模型预测控制器(MPC)和底层的鲁棒反馈线性化控制器组成该MPC控制器,生成满足所有相关约束的优化无碰撞状态参考轨迹,该方法对输入扰动具有鲁棒性,而且鲁棒反馈线性化控制器跟踪最优状态参考,抑制MPC更新区间内的跟踪误差[6]。Jiang等提出了基于机载传感器和嵌入式控制器的室外自主编队飞行的高效轨迹规划算法和集中控制方案。具体而言,研究了最优互避碰(ORCA)算法,以避免无人机在编队切换过程中的碰撞[7]。魏扬等针对无人机在三维空间内机动飞行时的编队队形保持问题,利用无人机自动驾驶仪模型和编队运动学模型,设计了一种编队保持的自适应控制器[8]。谢文光等针对多无人机编队控制问题提出了一种改进深度神经网络的飞行控制方法。该方法在控制器中加入动量因子,提高了网络的学习性能,仿真结果表明该控制器效果较好[9]。Wang等利用对偶数,考虑平移运动与旋转运动之间的耦合效应,对跟随航天器相对于先导航天器的六自由度运动进行了建模。并在该模型的基础上,提出了一种鲁棒自适应终端滑模控制律,包括自适应算法,以保证在存在模型不确定性和外部扰动的情况下,相对运动跟踪误差的有限时间收敛[10]。针对无人机设计的编队控制器都是保证速度可控,虽然不能直接将方法用到导弹上,但是可以给多弹编队控制器的设计提供思路。
目前针对多弹编队控制器设计的文献相对较少。采用领弹-从弹的编队模式,马培蓓和韦常柱等利用导弹的自动驾驶仪分别设计了基于线性反馈[11]和最优控制理论[12]的编队控制器,但是该方法要求导弹速度可控。张磊等通过微分几何理论将导弹的非线性运动模型进行线性化,并且在此基础上建立了基于导弹跟踪误差和相对误差的控制系统状态方程,在领弹推力方向上加入了速度控制项,采用领弹-从弹的制导策略,利用自适应滑模控制理论设计了编队控制器[13]。张磊等利用领弹-从弹策略,采用仿射非线性系统最优控制理论设计了编队控制器[14]。周慧波等针对导弹编队系统外部扰动和模型不确定性的情况,结合位置跟踪误差和速度跟踪误差设计了一种辅助误差变量,并在辅助误差变量的基础上提出了一种基于有向通信拓扑的鲁棒自适应编队控制策略,仿真结果表明该策略下的队形跟踪误差较小[15]。彭明星等设计了2种基于领弹-从弹法的多弹编队飞行控制方法,第一种是利用领从弹间的相对位置根据误差反馈设计了一种编队控制器,第二种方法是根据领弹、从弹和目标位置关系设计了一种编队控制器,仿真验证了这2种方法的有效性[16]。上述方法都可以实现编队队形的形成与保持,但都需要对导弹的速度进行控制,这不符合现实中导弹速度不可控这一先决条件。
本文在导弹速度不可控的前提要求下,首先在惯性系下定义领弹和从弹的相对位置以及编队控制器的状态变量,并且设计了编队控制系统。为了得到该系统的具体表达式,将导弹的俯仰和偏航通道加速度由弹道坐标系转到惯性坐标系下;其次采用滑模变结构控制理论和自适应动态面控制理论分别对领弹和从弹进行制导律设计;最后,针对中制导段领弹攻击预测命中点,采用1枚领弹、2枚从弹进行仿真,仿真结果验证了该方法的可行性和有效性。
1 导弹编队控制器设计模型
1.1 导弹编队控制器设计基础
单枚导弹在中制导段可能出现探测视场角较小,导弹截获目标概率较低的情形, 为了提高导弹在中制导段截获目标的概率,采用多枚导弹进行编队,同时对目标进行观测。下面给出导弹攻击目标的弹目相对运动关系如图 1所示。图中, Oxyz代表惯性坐标系, Ox2y2z2代表弹道坐标系, M和T分别代表导弹和目标, θ和ψV分别代表弹道倾角和弹道偏角。
导弹由惯性坐标系到弹道坐标系的变换矩阵可通过两次旋转求得。首先将地面坐标系绕Oy轴旋转一个ψV角, 然后绕Oz2轴旋转一个θ角, 可以得到惯性坐标系与弹道坐标系之间的转换矩阵为
导弹的运动学方程如下
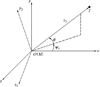 |
图 1 三维攻击几何 |
1.2 导弹编队控制器设计模型
本文采用领从式制导策略进行编队控制器设计。领弹和从弹的信息传递是单向的, 从弹能够接收领弹信息, 领弹不能接收从弹信息, 其在已设计好的制导律下攻击目标。领弹和第i枚从弹在惯性坐标系下的相对位置关系如图 2所示。
图 2中, Ml和Mfi分别代表领弹和第i枚从弹, Xl, Yl和Zl分别代表领弹在惯性系下x, y和z方向上的坐标值, Xfi, Yfi和Zfi分别代表第i枚从弹在惯性系下x, y和z方向上的坐标值, ΔXi, ΔYi和ΔZi分别代表领弹和第i枚从弹在惯性系下x, y和z方向上的相对位置差值。下面给出ΔXi, ΔYi和ΔZi的表达式。
定义状态变量 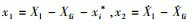 ,
, 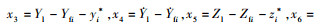
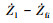 , 其中, xi*, yi*和zi*分别代表惯性系下领弹和第i枚从弹在x, y和z方向上的期望相对位置差值, 则三维空间内的编队控制问题的控制系统可以表示为
, 其中, xi*, yi*和zi*分别代表惯性系下领弹和第i枚从弹在x, y和z方向上的期望相对位置差值, 则三维空间内的编队控制问题的控制系统可以表示为
式中: axl, ayl和azl分别代表领弹在惯性系下x, y和z方向上的加速度; axfi, ayfi和azfi分别代表第i枚从弹在惯性系下x, y和z方向上的加速度。
假设领弹在弹道坐标系下的俯仰通道和偏航通道加速度分别为anyl和anzl, 第i枚从弹在弹道坐标系下的俯仰和偏航通道加速度分别为anyfi和anzfi。根据惯性坐标系转换到弹道坐标系的变换矩阵, 可以得到由弹道坐标系变换到惯性坐标系的转换矩阵。
将领弹和从弹弹道坐标系下的加速度转换到惯性系下, 得
将(5)式代入(6)式和(7)式中, 得到领弹和第i枚从弹在惯性坐标系下x, y和z方向加速度的具体表达式如下:
将(8)式和(9)式代入(4)式中, 可以将控制系统表示为
观察(10)式, 对其进行推理与转换, 可以得到控制系统的具体表达式。
为了后续控制器设计的简便, 对(11)式进行简化, 令
将上述简化量代入(11)式中, 可以得到控制系统的简化形式。
观察(12)式, 可以将其近一步化简, 令
将上述矩阵代入(12)式中, 可以得到控制系统的最终简化模型。
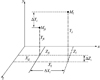 |
图 2 领弹和从弹的相对位置关系 |
2 多弹编队控制器设计
本文采用领弹-从弹的编队模式, 领弹和从弹的编队控制器分别采用滑模变结构控制理论和动态面控制器设计理论进行设计, 最终得到基于领从式制导策略的编队控制器。
2.1 领弹控制器设计
领弹采用文献[17]中的滑模变结构理论进行控制器设计, 具体形式如下。
式中:rl和 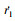 分别代表领弹与目标的弹目距离和弹目距离变化率;
分别代表领弹与目标的弹目距离和弹目距离变化率;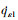 和
和 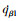 分别代表领弹的视线倾角变化率和视线偏角变化率;r1l=rcosqεl, m>0, n>0, δ1和δ2均为小正数。
分别代表领弹的视线倾角变化率和视线偏角变化率;r1l=rcosqεl, m>0, n>0, δ1和δ2均为小正数。
2.2 从弹控制器设计
针对上节推导出的编队控制器模型, 本节以第i枚从弹为例, 考虑到(13)式具有严格反馈形式, 下面采用自适应动态面控制算法完成多弹编队控制系统设计。
1) 定义第一个动态面s1i为
式中:s1i∈R3×1, X1i为系统状态变量。
对(16)式微分, 动态面s1i的一阶导数为
将(17)式中的状态变量X2i作为X1i的虚拟控制输入, 设计虚拟控制指令X2ic为
式中, 动态面增益矩阵k1i=diag(k11i, k21i, k31i), k11i, k21i和k31i均为待设计正常数。
2) 定义第二个动态面s2i为
式中:s2i∈R3×1, 实质为惯性系下速度的跟踪误差;X2i为系统状态变量。
对(19)式微分, 有
设计系统的控制输入ui为
式中,动态面增益矩阵k2i=diag(k12i, k22i, k32i), k12i, k22i和k32i均为待设计正常数。
结合(16)~(21)式, 得到多弹编队控制器自适应动态面控制算法如下
2.3 稳定性分析
采用Lyapunov稳定性理论, 对2.2节设计的编队控制器表达(22)式进行稳定性分析。
取V(0)≤p, p>0, 则闭环系统所有信号有界, 收敛。
证明: 对动态面s1i求导, 有
对动态面s2i求导, 有
定义如下Lyapunov函数
对(25)式进行求导, 得
取正数r, 若选择的参数满足
则
由于此时V=p, 则(28)式可写成 ≤-rp。由于r>0且p>0, 所以
≤-rp。由于r>0且p>0, 所以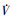 ≤0。(28)式说明当r>0时, V也在紧集之内, 即如果V(0)≤p, 则
≤0。(28)式说明当r>0时, V也在紧集之内, 即如果V(0)≤p, 则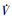 ≤0, 从而V(t)≤p。
≤0, 从而V(t)≤p。
由Lyapunov稳定性理论可知, 系统在有限时间内趋于稳定, 即当t→∞时, X1i→0。
由(29)式可得, 领弹和第i枚从弹在惯性坐标系下x, y和z方向的相对位置差值最终分别收敛到各方向的期望值。
下面进行收敛性分析, 首先给出引理1:
引理1[18] 针对V: [0, ∞)∈R, 不等式方程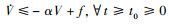 的解为
的解为
式中, α为任意常数。
上述引理的证明过程如下:
取 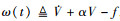 ,则ω(t) ≤0,且
,则ω(t) ≤0,且
解为
由于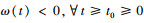 , 则
, 则
注: 如果f=0, 则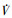 ≤-αV的解为
≤-αV的解为
如果α是正实数, 则V(t)以指数的形式收敛于零。由(28)式可知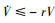 , 根据引理1, 不等式方程
, 根据引理1, 不等式方程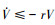 的解为
的解为
即
由(36)式可知, V(t)渐进收敛到零。
3 仿真验证
为了论证速度不可控条件下多弹编队协同控制方法的可行性和有效性, 本文设计了仿真验证试验。由1枚领弹和2枚从弹组成编队队形, 针对领弹在中制导过程中攻击预测命中点的场景, 要求2枚从弹在有限时间内与领弹形成期望的编队队形。导弹的初始参数信息如表 1所示, 假设预测命中点位于(0, 5 000, 0)点, 且静止, 领弹和从弹的速度均为1 000 m/s, 且速度保持不变, 加速度最大幅值均为AM=40g, 仿真步长为0.01 s。
针对表 1所示的3枚导弹, 领弹的滑模系数选取如下: m=5, n=10, δ1=δ2=0.002 5, 从弹的参数为k11=diag[10 1 5], k21=diag[1 15 0.5], k12=diag[25 15 5], k22=diag[0.5 10 5]。领弹和第一枚从弹的期望位置差为x1*=0, y1*=0, z1*=6 000, 领弹和第二枚从弹的期望位置差为x2*=0, y2*=0, z2*=-6 000, 利用(22)式所示控制器形式进行仿真, 结果如图 3至8所示, 具体的领弹和从弹相对位置与期望值之间的误差如表 2所示。并且为了体现本文设计编队控制器的性能, 与文献[16]中现有速度可控的编队控制器进行仿真对比, 两者的仿真初始条件均相同。文献[16]的编队控制器仿真结果如图 9至13所示, 具体的编队误差如表 2所示。
如图 3所示,领弹以滑模变结构控制对预测命中点进行攻击,整体轨迹较为平滑,反映到图 4所示的领弹加速度曲线上,其俯仰通道和偏航通道曲线均较为平滑。2枚从弹都在初始阶段轨迹迅速变化,在有限时间内达到预先设定的期望值,此时轨迹平滑。反映到图 5和图 6上,2枚从弹的加速度曲线都会在初始段剧烈变化,当达到队形要求后,曲线平滑。
图 7和图 8分别为领弹和2枚从弹位置差值与期望值的误差,可以发现2枚从弹均会在有限时间内达到误差为零,结合表 2,可以发现从弹1的跟踪误差较小,从弹2最大误差为13.4 m,相对于速度为1 000 m/s来说,误差较小,表明本文设计的编队控制器效果较好。对比图 7至8和图 12至13,可以发现本文方法相较于文献[16]方法,收敛时间会慢一些,但是差距不大。由图 12至13和表 2可以发现,本文提出的编队控制器也能够达到与文献[16]中控制器的控制精度。
图 3和图 9分别代表本文控制器和文献[16]现有要求速度可控编队控制器的三维轨迹图,可以发现,2种方法均能在有限时间内达到编队队形,并且此后保持该队形。观察图 10至11发现,文献[16]控制器算法为了达到期望队形,需要对导弹的速度实时控制,这对当前的技术提出了巨大的挑战,而且增加了能量的消耗。所以在不控制速度的条件下,本文提出的算法可以降低能量消耗,编队控制效果与现有方法相近,并且更便于应用到实际中去。
导弹参数信息
 |
图 3 3枚导弹轨迹图 |
 |
图 4 领弹加速度曲线 |
 |
图 5 从弹1加速度曲线 |
 |
图 6 从弹2加速度曲线 |
 |
图 7 领弹与从弹1相对位 |
 |
图 8 领弹与从弹2相对位置与期望值误差置与期望值误差 |
编队误差信息
4 结论
在导弹速度不可控这一前提下,本文采用领弹-从弹的编队模式,基于滑模变结构控制理论和自适应动态面控制理论分别对领弹和从弹的编队控制器进行设计。通过1枚领弹和2枚从弹的编队形式进行仿真,结果表明该制导律在响应速度和稳定性上效果都较好。而且本文提出的编队控制器不对导弹速度做要求,更便于应用到实际中。然而,本文并未考虑编队系统存在的扰动问题,控制器设计也是仅限于三自由度,这是今后进一步需要做的工作。
References
- TahkM, ParkC S, RyooC K. Line-of-sight guidance laws for formation flight[J]. Journal of Guidance, Control and Dynamics, 2005, 28(4): 708–716 [Article] [Google Scholar]
- DoganA, VenkataramananS. Nonlinear control for reconfiguration of unmmaned-aerial-vehicle formation[J]. Journal of Guidance, Control and Dynamics, 2005, 28(4): 667–678 [Article] [Google Scholar]
- Giulietti F, Innocenti M, Napolitano M, et al. Dynamic and control issues of formation flight[J]. Aerospace Science and Technology, 2005, 9: 65–71 [Article] [Google Scholar]
- Ajoulou A, Moezzi K, Aghdan A G, et al. Two-stage energy-optimal formation reconfiguration strategy[J]. Automatica, 2012, 48: 2587–2591 [Article] [Google Scholar]
- AjorlouA, MoezziK, AghdamA G, et al. Two-stage time-optimal formation reconfiguration strategy[J]. System & Control Letters, 2013, 62: 496–502 [Article] [Google Scholar]
- Zhao Weihua, Go T H. Quadcopter formation flight control combining MPC and robust feedback linearization[J]. Journal of the Fronklin Institute, 2014, 351(3): 1335–1355 [Article] [Google Scholar]
- Jiang Zeyu, Cheng Hui, Zheng Zefeng, et al. Autonomous formation flight of UAVs: control algorithms and field experiments[C]//Proceedings of the 35th Chinese Control Conferece, 2016 [Google Scholar]
- Wei Yang, Xu Haojun, Xue Yuan. Adaptive disturbance rejection controller design for UAV three dimensional formation keeping[J]. Systems Engineering and Electronics, 2018, 40(12): 2758–2765 [Article] (in Chinese) [Google Scholar]
- Xie Wenguang, Wu Kang, Yan Fang, et al. A Formation flight method with an improved deep neural network for multi-UAV system[J]. 2020, 38(2): 295–302 (in Chinese) [Google Scholar]
- Wang Jianying, Sun Zhaowei. 6-DOF robust terminal sliding mode control for spacecraft formation flying[J]. Acta Astronautica, 2012, 73: 76–87 [Article] [Google Scholar]
- Ma Peibei, Ji Jun. Three-dimensional multi-missile formation control[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(8): 1660–1666 [Article] (in Chinese) [Google Scholar]
- Wei Changzhu, Guo Jifeng, Cui Naigang. Research on the missile formation keeping optimal control for cooperative engagement[J]. Journal of Astronautics, 2010, 31(4): 1043–1050 [Article] (in Chinese) [Google Scholar]
- Zhang Lei, Fang Yangwang, Mao Donghui, et al. Adaptive sliding-mode controller design for missile cooperative engagement[J]. Journal of Astronautics, 2014, 35(6): 700–707 [Article] (in Chinese) [Google Scholar]
- Zhang Lei, Fang Yangwang, Diao Xinghua, et al. Design of nonlinear optimal controller for multi-missile formation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(3): 401–406 [Article] (in Chinese) [Google Scholar]
- Zhou Huibo, Song Shenmin, Zheng Zhong. Distributed robust adaptive control for missile cooperative engagement within formation[J]. Journal of Chinese Inertial Technology, 2015, 23(4): 516–527 [Article] (in Chinese) [Google Scholar]
- Peng Mingxing, Wu Yunjie, Zhu Futao. Research on control method for anti-ship missiles formation flight[J]. Journal of System Simulation, 2017, 29(1): 212–217 [Article] (in Chinese) [Google Scholar]
- Xiong Ke, Guo Zhenyun. A variable structure terminal guidance law of anti-mobile missile in atmosphere[C]. //Proceedings of the Annual Conference of Flight Mechanics and Flight Test Academic Exchange, 2006 (in Chinese) [Google Scholar]
- Liu Jinkun. Sliding mode control design and MATLAB simulation[M]. [3rd Edition]. Beijing: Tsinghua University Press, 2015 [Google Scholar]
All Tables
All Figures
 |
图 1 三维攻击几何 |
| In the text | |
 |
图 2 领弹和从弹的相对位置关系 |
| In the text | |
 |
图 3 3枚导弹轨迹图 |
| In the text | |
 |
图 4 领弹加速度曲线 |
| In the text | |
 |
图 5 从弹1加速度曲线 |
| In the text | |
 |
图 6 从弹2加速度曲线 |
| In the text | |
 |
图 7 领弹与从弹1相对位 |
| In the text | |
 |
图 8 领弹与从弹2相对位置与期望值误差置与期望值误差 |
| In the text | |
 |
图 9 文献[16]方法中3枚 |
| In the text | |
 |
图 10 文献[16]方法中从弹1 |
| In the text | |
 |
图 11 文献[16]方法中从弹2导弹轨迹图速度跟踪曲线速度跟踪曲线 |
| In the text | |
 |
图 12 文献[16]方法中领弹与从弹1相对位置与期望值误差 |
| In the text | |
 |
图 13 文献[16]方法中领弹与从弹2相对位置与期望值误差 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


